1. Particule isolée. Moment cinétique
Pour une particule isolée, l’axe \(Z\) est un axe privilégié, car cette composante est mesurable (avec un champ magnétique infiniment petit, par exemple, cet axe est alors parallèle au champ). Il apparaît un nombre quantique de spin \(s\) : \[M_c=\sqrt{s~(s+1)}~\hbar\quad;\quad\hbar=\frac{h}{2~\pi}\]
La composante \(M_{c,z}\) peut prendre (\(2~s+1\)) valeurs : \[M_{c,~z}=s_z~\hbar\quad;\quad s_z=\{-s,~-s+1,~\dots,~s-1,~s\}\]
Le moment cinétique apparaît donc comme un vecteur quantique de module : \[\sqrt{s~(s+1)}~\hbar\qquad\text{et non pas :}\quad s~\hbar\]
Il peut prendre (\(2~s+1\)) composantes selon l’axe \(Z\), la plus grande étant \(s~\hbar\) et on ne peut connaître les autres composantes \(s_x\) et \(s_y\).
2. Particule isolée. Moment magnétique
2.1. Définitions
Le moment magnétique est proportionnel au moment cinétique : \[M_m=\frac{e}{2~m}~M_c\]
L’expérience confirme ce résultat à un facteur \(g\) près appelé facteur de Landé déterminé expérimentalement par la spectroscopie. Ce facteur est de l’ordre de l’unité (pour un électron libre). On a donc : \[M_m=\sqrt{s~(s+1)}~g~\mu\quad;\quad M_{m,~z}=s_z~g~\mu\]
Le paramètre \(\mu\) est le magnétron : \[\mu=\cfrac{e~\hbar}{2~m}\]
Pour le magnétron de Bohr de l’électron : \[\mu_B=\cfrac{e~\hbar}{2~m_e}\]
Pour les particules plus lourdes (proton), on se réfère au magnétron nucléaire : \[\mu_N=\cfrac{e~\hbar}{2~m_p}\]
2.2. Particule placée dans une induction magnétique B
La particule placée dans l’induction \(B\) (orientée selon l’axe \(Z\)) peut prendre \((2s+1)\) énergies possibles : \(s_z~g~\mu~B\).
La théorie classique nous apprend que la dérivée par rapport au temps du moment cinétique est égale au moment des forces appliquées : \[\frac{d}{dt}(\overrightarrow{M_c})=M_m\wedge\overrightarrow{B}=\frac{e}{2~m}~(\overrightarrow{M_c}\wedge\overrightarrow{B})\]
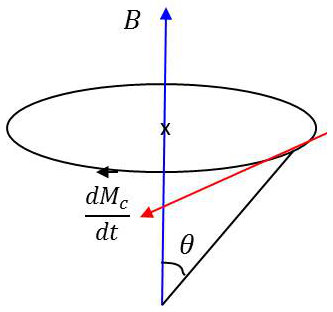 Le moment cinétique tourne autour du vecteur \(B\) avec une vitesse angulaire \(\omega_L\). \[\frac{d}{dt}(\overrightarrow{M_c})=\overrightarrow{\omega_L}\wedge\overrightarrow{M_c} \quad\Rightarrow\quad\overrightarrow{\omega_L}=-\frac{e~\overrightarrow{B}}{2~m}\]
Le moment cinétique tourne autour du vecteur \(B\) avec une vitesse angulaire \(\omega_L\). \[\frac{d}{dt}(\overrightarrow{M_c})=\overrightarrow{\omega_L}\wedge\overrightarrow{M_c} \quad\Rightarrow\quad\overrightarrow{\omega_L}=-\frac{e~\overrightarrow{B}}{2~m}\]
\(\overrightarrow{\omega_L}\) est la pulsation de Larmor, égale à la vitesse angulaire de précession du moment magnétique autour de \(\overrightarrow{B}\).
On remarque que : \[\hbar~\overrightarrow{\omega_L}=-\mu~\overrightarrow{B}\qquad\text{énergie d'un magnétron parallèle à }\overrightarrow{B}\]
3. Systèmes de particules et oscillateurs
3.1. Comparaison avec la mécanique classique
Les systèmes de particules en interaction présentent certains caractères des systèmes vibrants et oscillants.
Une corde vibrante, une tige encastrée présentent des fréquences propres qui sont les multiples de la fréquence fondamentale. Les systèmes à 2 ou 3 dimensions (plaque, disque, cylindre, cube, sphère, etc.) possèdent également des fréquences propres qui ne sont pas toujours dans un rapport simple entre elles. Chaque mode est alors caractérisé respectivement par 2 ou 3 nombres.
Ainsi, pour une cavité électromagnétique trirectangulaire les fréquences de résonance sont : \[\nu_{l,~m,~n}=c~\sqrt{\frac{l^2}{4~a^2}+\frac{m^2}{4~b^2}+\frac{n^2}{4~c^2}}\]
Si l’on couple deux systèmes vibrants identiques, on constate que les fréquences de résonance se dédoublent (circuits oscillants radio couplés, pendules identiques supportés par une lame élastique, etc.)
Ainsi, deux électrons d’un même atome ne peuvent être dans le même état. Ou encore, les électrons des divers atomes identiques rassemblés dans un solide possèdent des modes de fréquence propre élargis en bande quoique étant issus d’un même mode relatif aux atomes isolés.
3.2. Équation de Schrödinger
L’équation de Schrödinger est la relation fondamentale entre les fonctions d’ondes et les énergies des différents états que peut prendre une particule dans une énergie potentielle connue \(W(x,~y,~z)\) : \[-\frac{h^2}{8~\pi^2~m}~\Delta\Psi_0+W(x,~y,~z)~\Psi_0=E~\Psi_0\]
Elle n’admet de solutions \(\Psi_0\) bornées à l’infini que pour certaines valeurs de l’énergie \(E\).
3.2.1. Oscillateur linéaire à une dimension
Une particule de masse \(m\) oscillant sur un axe et soumise à une force de rappel proportionnelle à son élongation \(f=-k~x\) et a une énergie potentielle \(W=k~x^2/2\). On peut considérer qu’elle vibre à la fréquence fondamentale : \[\nu_0=\frac{1}{2~\pi}~\sqrt{\frac{k}{m}}\]
avec une énergie : \[E=\frac{k^2~a^2}{2}=2~\pi^2~m~a^2~\nu_0^2\qquad\text{(a~: amplitude quelconque)}\]
On peut aussi considérer l’oscillateur par son équation de Schrödinger : \[-\frac{h^2}{8~\pi^2~m}~\frac{\partial^2}{\partial x^2}(\Psi_0)+\frac{k~x^2}{2}~\Psi_0=E~\Psi_0\quad;\quad k=m~\omega_0^2\]
Celle-ci n’admettant de solutions bornées nulles à l’infini que pour certaines valeurs de l’énergie : \[E_n=(n+\frac{1}{2})~h~\nu_0\]
avec : \[\Psi_n(x)=\Big(\frac{m~\omega}{\hbar}\Big)^{1/4}~u_n\Big(x\sqrt{\frac{m~\omega}{\hbar}}\Big)\]
\(u_n(q)\) étant le polynôme d’Hermite d’ordre \(n\) : \[u_n(q)=(\sqrt{\pi}~2^n~n!)^{-1/2}~\Big(q-\frac{d}{dq}e^{-q^2/2}\Big)\]
L’état de l’oscillateur dépend du nombre quantique \(n\). On connaît les propriétés de l’oscillateur en étudiant son absorption (ou son émission d’énergie) qui se fait par quanta : \[\Delta E=E_n-E_m=(n-m)~h~\nu_0\]
Exemples
-
Si l’énergie se présente sous forme de rayonnement électromagnétique, chaque quantum \(h~\nu_0\) correspond à un photon.
-
Si l’énergie est sous forme d’une onde élastique (vibration thermique des cristaux), chaque quantum \(h~\nu_0\) est un phonon.
3.2.2. Atome d’hydrogène
On peut associer aux noyaux atomiques d’autres nombres quantiques :
– Le nombre \(I\) donnant le moment cinétique du noyau : \[M_c=\sqrt{I~(I+1)}~\hbar\]
– Le nombre \(I_Z\) donnant la composante suivant l’axe de quantification : \[M_{c,~z}=I_z~\hbar\qquad \{I_z=-I,~-I+1,~+I\}\]
L’atome d’hydrogène est un système à 3 dimensions. On doit s’attendre à voir apparaître 3 nombres quantiques dans la résolution de l’équation de Schrödinger : \[-\frac{h^2}{8~\pi^2~m}~\Delta\Psi_0-\frac{e^2}{4~\pi~\varepsilon~r^2}~\Psi_0=E~\Psi_0\]
Les solutions propres sont : \[\Psi_0^{n,~l,~m}(r,~\theta,~\varphi)=a^{-3/2}~y^{m,~l}(\theta,~\varphi)~y_{n,~l}\Big(\frac{2r}{n~a}\Big)\]
avec :
\[\begin{aligned} a&=\frac{4~\pi~\varepsilon_0~h^2}{m~e^2}\\ \qquad\\ y^{m,~l}(\theta,~\varphi)&=(-1)^m~\Big\{\frac{2~l+1}{4~\pi}~\frac{(l-m)!}{(l+m)!}\Big\}^{1/2}~P_l^m(\cos\theta)~e^{-j~m~\varphi}\\ P_l^m(u)&=(1-u^2)^{m/2}~\frac{d^m}{du^m}\Big\{\frac{1}{2^l~l!}~\frac{d^l}{du^l}~(u^2-1)^l\Big\}\\ \qquad\\ y_{n,~l}(x)&=\frac{2}{n^2}~\sqrt{\frac{(n-l-1)!}{[(n+l)!]^3}}~x^l~e^{-x/2}~L_{n-l-1}^{2l+1}(x)\\ L_p^k(x)&=(-1)^k~\frac{q^k}{dx^k}\Big\{e^x\frac{d^{p+k}}{dx^{p+k}}(e^{-x}~x^{p+k})\Big\}\end{aligned}\]
Les trois nombres quantiques \(n,~l,~m\) sont caractérisés de la manière suivante :
-
Le nombre quantique principal \(n =1,~2,~3,~\dots\) indique la couche \(K,~L,~M,~\dots\) sur laquelle gravite l’électron. À l’état \(n\) correspond l’énergie : \[E_n=-\frac{1}{n^2}~\frac{2~\pi^2~m~e^4}{(4~\pi~\varepsilon)^2~h^2}\]
L’état le plus stable est celui d(énergie minimum (\(n=1\)).
-
Le nombre quantique azimutal \(0~\leq~l~<~n\), soit \(l=0,~1,~2,~\dots,~(n-1)\). Ce nombre décrit l’orbite électronique (électron \(s, p, d, f …\)) et donne :
– Le moment cinétique orbital : \[M_{c,o}=\sqrt{l~(l=1)}~\hbar\]
– Le moment magnétique orbital : \[M_{m,o}\approx\mu_B~\sqrt{l~(l+1)}\]
-
Le nombre quantique \(m\) (ou \(l_z\)) compris entre (\(-l\)) et (\(+l\)), soit \(m = -l,~-l+1,~\dots,~-1,~0,~+1,~\dots,l\). Il donne, sur l’axe privilégié, les deux composantes :
\[\begin{aligned} &M_{c,~oz}=m~\hbar\qquad\text{ou encore :}\quad l_z~\hbar\\ &M_{m,~oz}=m~\mu_B\qquad\text{ou encore :}\quad l_z~\mu_B\end{aligned}\]
Les moments cinétiques et magnétiques résultent de la contribution orbitale et spinorielle.
4. Atomes et ions quelconques
Pour les atomes et les ions, les règles générales sont celles de l’atome d’hydrogène, mais l’énergie a une forme plus compliquée :
-
Chaque électron est dans un niveau \(n=1~,2,~3,~\dots\) selon qu’il se trouve sur l’un des niveaux \(K,~L,~M,~\dots\)
-
Un électron d’une couche \(n\) peut avoir un nombre quantique \(l=0,~1,~2,~\dots,~(n-1)\}\). Il est alors dans l’état \(s,~p,~d,~f,~\dots\)
-
Un électron dans l’état \(l\) peut se présenter sous différents états \(l_z=-l,~-l+1,~\dots,~l-1,~l\).
-
Sa composante de spin peut prendre les valeurs \(S_z=\pm1/2\).
-
Généralement, dans le couplage normal dit de Russel–Saunders, le moment cinétique orbital de l’ion est obtenu en composant les moments orbitaux de chacun des électrons. Il est donné par le nombre quantique \(L\) : \[M_{orb}=\sqrt{L~(L+1)}~\hbar\]
Si \(L=0,~1,~2,~3,~\dots\), on dit que l’ion ou l’atome est dans l’état \(S,~P,~D,~F,~\dots\)
De même, le moment cinétique de spin total est obtenu en composant les spins de chaque électron et est donné par le nombre quantique \(S\) : \[M_{c,~spin}=\sqrt{S~(S+1)}~\hbar\]
Le moment cinétique global de l’atome ou de l’ion est obtenu en combinant les deux moments d’orbite et de spin et est défini par le nombre quantique \(J\) : \[J=L\pm S\]
Le signe est choisi selon une règle qui ne sera pas précisée ici.
Dans tous les cas, même en dehors du couplage normal :
-
Le moment cinétique est : \[M_c=\sqrt{J~(J+1)}~\hbar\]
-
Sa composante suivant \(oz\) est : \[M_{c,~z}=J_z~\hbar\quad;\quad J_z=-J,~-J+1,~\dots,~+J\]
-
Le moment magnétique est : \[M_m=g~\sqrt{J~(J+1)}~\mu_B\]
-
La composante suivant \(oz\) est : \[M_{m,~z}=g~J_z~\mu_B\]
\(g\) : facteur de Landé (\(1<g <2\)) dont la valeur peut être approchée théoriquement.
Exemple
En notation spectroscopique, on dit que l’ion \(F^{++}\) est dans l’état \(^5D_4\).
\(D\) pour \(L=2\) ; \(4\) pour \(J\) ; \(5\) pour \((2~S+1)\) avec \(S=2\).
5. Principe d’exclusion de Pauli. Classification de Mendeleïev
5.1. Principe d’exclusion
Deux particules de spin demi-entier impair (1/2, 3/2, 5/2, ...) en interaction ne peuvent se trouver dans le même état.
On voit l’analogie avec deux systèmes oscillants identiques couplés mutuellement.
5.2. Classification de Mendeleiev
On applique cette règle en construisant des atomes neutres à nombre d’électrons croissants.
On sait que \(l\) peut varier de \(0\) à \((n-1)\), donc :
-
Dans le niveau K, on ne peut mettre que des électrons \(s\).
-
Dans le niveau L, on ne peut mettre que des \(s\) et \(p\).
-
Dans le niveau M, on ne peut mettre que des \(s\), \(p\) et \(d\).
-
Dans le niveau N, on ne peut mettre que des \(s\), \(p\), \(d\) et \(f\).
De même, \(l_z\) ne peut varier que de (\(-l\)) à (\(+l\)), ce qui signifie que sur un niveau élevé on ne peut mettre que :
-
2 électrons \(s\) (\(l=0\)) de spins antiparallèles.
-
6 électrons \(p\) (\(l=1\)) un couple d’électrons pour \(l_z=-1,~0,~+1\).
-
10 électrons \(d\) (\(l=2\))un couple d’électrons pour \(-2,~-1,~0,~+1,~+2\).
Ainsi, la notation \(1s^2~2s^2~p^6~3s^1\) signifie que l’on trouve :
-
Niveau K (n=1) 2 électrons \(s\) (l=0)
-
Niveau L (n=2) 2 électrons \(s\) (l=0) et six électrons \(p\) (l=1)
-
Niveau M (n=3) 1 électron \(s\) (l=0)
Sur le niveau K, le remplissage donne : \[H(1s^1)~H_e(1s^2)\]
Sur le niveau L, en admettant la couche K complète : \[Li(2s^1)~Be(2s^2)~B(2s^2p^1)~C(2s^2p^2)~N(2s^2p^3)~O(2s^2p^4)~F(2s^2p^5)~Ne(2s^2p^6)\]
Sur le niveau M, en omettant les couches K et L complètes : \[Na(3s^1)~Mg(3s^2)~Al(3s^2p^1)~Si(3s^2p^2)~P(3s^2p^3)~S(3s^2p^4)~Cl(3s^2p^5)~A(3s^2p^6)\]
Ici se produit un accident : la couche \(4s\) se remplit avant la couche \(3d\) : \[K(3s^2p^64s^1)~Ca(3s^2p^64s^2)\]
Puis on trouve les premiers éléments de transition : \[Sc(3s^2p^6d^14s^2)~Ti(3s^2p^6d^24s^2)~V~Cr~Mn~Fe~Co~Ni~Cu(3s^2p^6d^{10}4s^1)~Zn(3s^2p^6d^{10}4s^2)\]
Le niveau M est alors complètement rempli et on poursuit le remplissage du niveau N, etc., avec de nouveaux accidents aux terres rares et aux autres éléments de transition.
Remarque
La configuration des ions bivalents \(V^{++},~Cr^{++},~Mn^{++},~Fe^{++},~Co^{++},~Ni^{++},~Cu^{++}\) est obtenue en enlevant les 2 électrons \(4s\).
6. Statistiques quantiques
Par statistiques quantiques, on entend des deux statistiques suivantes :
-
la statistique de Fermi-Dirac à laquelle obéissent les particules de spin demi-entier impair (1/2, 3/2, 5/2, ...) ;
-
la statistique de Bose-Einstein à laquelle obéissent les particules de spin entier (photon).
On tient compte des faits suivants :
-
les particules élémentaires identiques sont indiscernables ;
-
les particules de spin demi-entier impair satisfont au principe d’exclusion de Pauli tandis que celles de spin entier n’y satisfont pas.
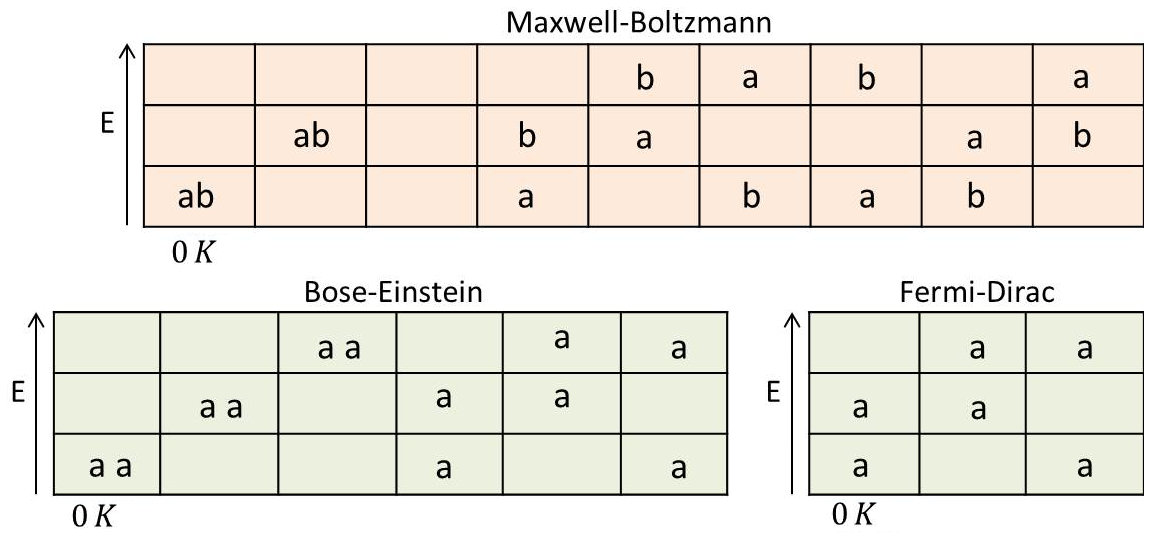 Le tableau ci-contre donne les complexions de deux particules pouvant être réparties dans trois cellules pour les diverses statistiques (chaque cellule représente un état).
Le tableau ci-contre donne les complexions de deux particules pouvant être réparties dans trois cellules pour les diverses statistiques (chaque cellule représente un état).
Noter que pour une particule : \[\Delta p_x~\Delta q_x~\geq~\frac{\hbar}{2}\]
On montre que dans l’espace des phases à 6 dimensions constitué par l’assemblage de l’espace réel (\(q_x~,~q_y~,~q_z\)) et de l’espace des quantités de mouvement (\(p_x,~p_y,~p_z\)), une particule occupe une cellule de volume fini égal à \(h^3\).
Pour un grand nombre de particules, on trouve que le taux d’occupation d’une cellule d’énergie \(E\) est donnée par la relation : \[\tau=\frac{1}{\cfrac{1}{A}~\exp\Big(\cfrac{E}{k~T}\Big)+\varepsilon} \quad;\quad\varepsilon~=~ \left\{ \begin{aligned} &-1\qquad\text{Bose-Einstein}\\ &~~~~0\qquad\text{Maxwell-Boltzmann}\\ &+1\qquad\text{Fermi-Dirac} \end{aligned} \right.\]
\(A\) est un facteur de normalisation pour la loi de probabilité.
On remarquera que : \[\text{si}~~k~T\gg E\qquad\Rightarrow\qquad\tau~\cong~A~\exp\Big(-\frac{E}{k~T}\Big)\]

