1. Généralités

Les lentilles sont très souvent de faible épaisseur, à l’exception de celles qui interviennent dans de nombreux instruments (microscopes par exemple).

Les lentilles peuvent être considérées comme l’association de deux systèmes optiques élémentaires, constituant les dioptres qui les limitent.

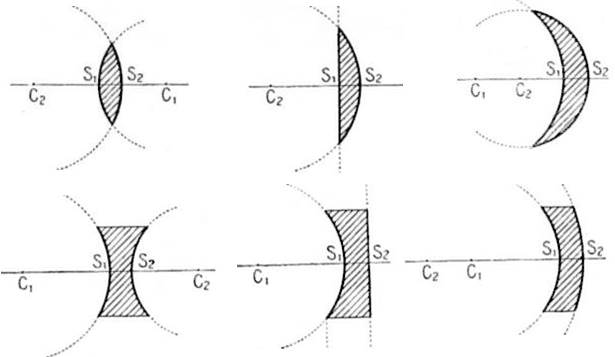
Une lentille est un système centré formé de deux dioptres dont l’un au moins est sphérique. On peut avoir six formes différentes de lentilles.

Les surfaces optiques qui limitent la lentille sont ses faces. L’axe de la lentille est la droite qui joint les centres de courbure \(C_1\) et \(C_2\) des faces. Si l’une des faces est plane, l’axe est la perpendiculaire menée à cette face, par le centre de la face courbe.

L’épaisseur de la lentille est la portion \(S_1S_2\) de l’axe comprise entre les deux faces. Si la lentille a une épaisseur négligeable devant les rayons de ses faces : elle est dite mince Elle est dite épaisse dans le cas contraire.

1.1. Le dioptre considéré comme un système centré

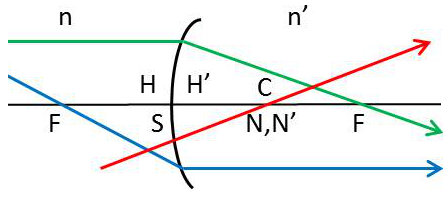Soit un dioptre de sommet S, de centre C séparant deux milieux d’indices n et n’. Le lieu de l’intersection d’un rayon incident parallèle à l’axe et du rayon émergent est le dioptre lui-même.

Il en résulte que les points principaux HH’ sont confondus en S.

D’autre part, un rayon passant par C n’est pas dévié : les points nodaux NN’ sont donc confondus en C.

Enfin la convergence du dioptre est : \[D=-\frac{n}{\overline{SF}}=\frac{n'}{\overline{SF'}}=\frac{n-n'}{r}\]

1.2. La lentille est un système centré

Une lentille possède naturellement toutes les propriétés générales des systèmes centrés. Elle est stigmatique, d’une façon approchée pour tout point qui ne lui envoie qu’un faisceau de rayons voisin de l’axe et peu incliné sur lui. D’un objet plan, perpendiculaire à l’axe et suffisamment petit, elle donne une image plane et perpendiculaire à l’axe.

Ce sont les conditions de l’approximation de Gauss, les seules étudiées dans le présent chapitre. Elle possède deux foyers, deux plans principaux, deux points nodaux et deux points antiprincipaux qui vont s’intervertir quand on change le sens dans lequel la lentille travaille.

2. Faisceau de rayons traversant une lentille épaisse

Soient F et F’ les foyers de la lentille, P et P’ ses plans principaux et A’B’ l’image, construite à la manière habituelle, d’un objet AB.

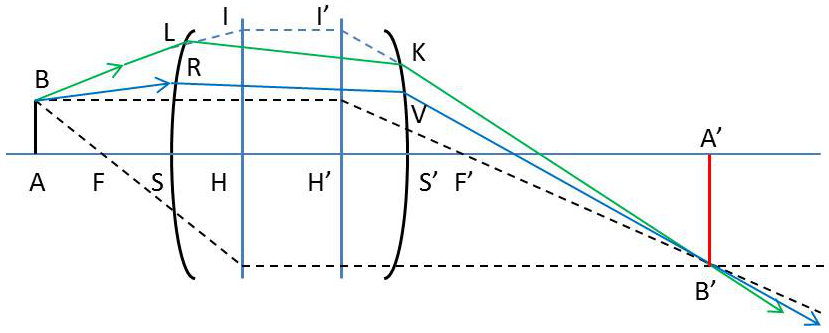Traçons un rayon incident quelconque BL, issu de B. Son support rencontre en I le plan principal objet.

L’image de I dans la lentille est le point I’ du plan principal image, situé du même côté de l’axe et à la même distance de cet axe que le point I. Le rayon émerge suivant I’B’.

Le rayon incident perce la face d’entrée S de la lentille au point L, son émergent perce la face de sortie S’ en K. Pour aller de L en K, la lumière, ne traversant qu’un seul milieu, se propage en ligne droite suivant LK.

Un deuxième rayon incident voisin, BR, se réfracte de même deux fois seulement en R et V, et limite avec BL, un faisceau de rayons dont la figure fait apparaître la marche.

Dans un système centré formé de plus de deux dioptres, la connaissance des plans principaux, des foyers et des faces extrêmes ne permet de construire que les parties BLR et KVB’ du faisceau extérieures au système. Le tracé de la marche du faisceau à l’intérieur du système n’est pas possible avec ces seules données.

3. Recherche des foyers et des plans principaux

La lentille est définie lorsqu’on connaît les caractéristiques des deux dioptres qui la forment et son épaisseur.

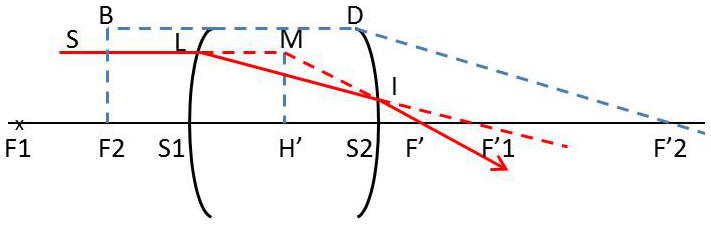On désigne par \(f_1,f'_1\) les distances focales objet et image du dioptre d’entrée \(S_1\) de foyer objet \(F_1\) et de foyer image \(F'_1\).

De même \(f_2,f'_2\) désignent les distances focales du dioptre \(S_2\) de foyers \(F_2\) et \(F'_2\).

La position de la face de sortie \(S_2\) par rapport à la face d’entrée \(S_1\) est définie par \(\overline{F'_2F_2}=\Delta\), abscisse du foyer objet \(F_2\) du dioptre \(S_2\) par rapport au foyer image \(F'1\) du dioptre \(S_1\).

3.1. Position du foyer image F’

Un rayon incident \(SL\) parallèle à l’axe rencontre en L la face d’entrée et se réfracte suivant \(LF'_1\). Il perce la face de sortie au point I, effectue une seconde réfraction et émerge suivant \(IF'\).

Pour construire géométriquement ce rayon, nous prenons le point d’intersection B du rayon \(LI\) avec le plan focal objet du dioptre \(S_2\) et nous menons par B la parallèle \(BD\) à l’axe ; le dioptre recevant le rayon \(BD\) le réfracte suivant \(DF'_2\) ; \(IF'\) est la parallèle menée de I à \(DF'_2\).

La position de F’ pourrait être déduite de cette construction. Cependant, on peut appliquer directement les résultats du chapitre précédent : \[\overline{F'_2F'}=\frac{f'_2f'}{-\Delta}\qquad\Rightarrow\qquad\overline{S_2F'}=f'_2~\big\{1- \frac{f_2}{\Delta}\big\}\]

Cette expression fixe sans ambiguïté la position du foyer image de la lentille par rapport à sa face de sortie. Son signe nous renseigne immédiatement sur la nature de ce foyer : il est réel si, avec les conventions de signes faites, \(S_2F'>0\) et virtuel dans le cas contraire.

3.2. Position du plan principal image

L’incident SL, parallèle à l’axe, et son émergent IF’ se coupent en M ; le plan de front passant par M est le plan principal image P’ ; soit H’ le point où il coupe l’axe. Cette construction permettrait de déterminer la position du plan principal image, mais le résultat ne présentant qu’un intérêt pratique médiocre, nous nous bornerons à déterminer la convergence.

3.3. Convergence

On peut connaître la distance focale image par la relation (chapitre précédent) : \[f'=\frac{-f_1~f'_2}{\Delta}\]

On peut d’autre part appliquer la relation de Gullstrand. Si \(r_1\) et \(r_2\) sont les rayons de courbure, n, N et n’ les indices successifs, on aura :

\[\begin{aligned} D_1&=\frac{N-n}{r_1}\quad~; \quad D_2=\frac{n'-N}{r_2}\\ D&=D_1+D_2-\frac{e}{N}~D_1~D_2\end{aligned}\]

3.4. Foyer objet. Plan principal objet. Distance focale objet.

En faisant tomber sur la lentille un rayon incident parallèle à l’axe qui, cheminant de droite à gauche, rencontrerait d’abord la face \(S_2\) puis la face \(S_1\), nous déterminerions de la même manière les positions du foyer objet et du plan principal objet. Les résultats cherchés s’obtiennent immédiatement à partir des formules précédentes dans lesquelles on fait les substitutions : \[f'_1\rightarrow f_2\quad;\quad f'_2\rightarrow f_1\quad;\quad f_2\rightarrow f'_1 \quad;\quad f_1\rightarrow f'_2\quad;\quad \Delta\rightarrow (-\Delta)\]

On trouve :

\[\begin{aligned} &\overline{S_1F}=\frac{f_1~(f'_1+\Delta)}{\Delta}\\ &f=\overline{HF}=\frac{f_2~f_1}{\Delta}\end{aligned}\]

Si \(\overline{S_1F}>0\), le foyer objet est virtuel. Il est réel dans le cas contraire.

Remarque

Reprenant les deux dernières expressions des distances focales, on peut écrire :

\[\begin{aligned} &\frac{f'}{f}=\frac{-f'_1~f'_2}{\Delta}\frac{\Delta}{f_2f_1}=-\frac{f'_1}{f_1}\frac{f'_2}{f_2}\\ &\frac{f'}{f}=-\frac{N}{n}\frac{n'}{N}=-\frac{n'}{n}\end{aligned}\]

Le rapport des distances focales est égal au rapport, changé de signe, des indices des milieux extrêmes.

4. Lentille épaisse en contact avec deux milieux identiques

La lentille épaisse en contact avec deux milieux identiques est un cas particulier d’une importance pratique considérable, car les faces des lentilles (généralement en verre) sont souvent baignées dans l’air.

Nous allons transformer les formules trouvées précédemment en faisant intervenir les rayons de courbure \(r_1\) et \(r_2\) des faces, l’épaisseur \(\overline{S_1S_2}=e\) de la lentille et son indice relatif N par rapport à l’extérieur.

Nous avons :

\[\begin{aligned} f_1=-\frac{r_1}{N-1} &\quad;\quad f'_1=\frac{N~r_1}{N-1}\\ f_2=\frac{N~r_2}{N-1}&\quad;\quad f'_2=-\frac{r_2}{N-1}\end{aligned}\]

D’où on déduira :

\[\begin{aligned} \overline{S_2F'}&=-\frac{r_2}{N-1}~\frac{N~r_1-(N-1)~e}{N~(r_1-r_2)-(N-1)~e}\\ \overline{S_1F} &=-\frac{r_1}{N-1}~\frac{N~r_2-(N-1)~e}{N~(r_2-r_1)-(N-1)~e}\end{aligned}\]

D’autre part : \[D_1=\frac{N-1}{r_1}\quad~; \quad D_2=\frac{N-1}{r_2}\]

On aura donc : \[D=(N-1)~\big\{\frac{1}{r_1}-\frac{1}{r_2}\big\}+\frac{{(N-1)^2}}{N}\frac{e}{r_1~r_2}\]

Remarque

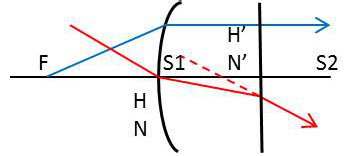Si l’une des faces de la lentille est plane, l’un des points principaux est le sommet de la face courbe. En effet, un rayon issu de F rencontre le rayon émergent parallèle à l’axe sur le dioptre courbe.

Le point principal H est donc en \(S_1\). Le point principal H’ est le conjugué de H dans le dioptre plan.

H’ est situé à la distance \(e~(N-1)/N\) de la face courbe et à la distance \(e/N\) de la face plane.

L’interstice HH’ est ici, en toute rigueur, égal à \(e~(N-1)/N\) quel que soit e. Il est clair d’autre part que le rayon incident passant par \(S_1\) et le rayon émergent passant par H’ sont parallèles : H et H’ sont bien confondus avec les points nodaux N et N’.

5. Centre optique

Le centre optique est le point O de l’axe tel que tout rayon qui passe par ce point après s’être réfracté sur la face d’entrée de la lentille, ressort parallèle à sa direction incidente.

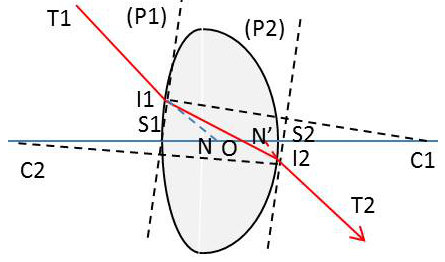Prenons par exemple une lentille biconvexe dont les faces \(S_1\) et \(S_2\) ont leurs centres respectifs en \(C_1\) et \(C_2\).

Soit \(I_1\) un point quelconque de la face d’entrée. \(C_1I_1\) est la normale en \(I_1\) à cette face. Menons \(C_2I_2\) parallèle à \(C_1I_1\).

\(C_2I_2\) est la normale en \(I_2\) à la face de sortie et les plans \(P_1\) et \(P_2\) tangents respectivement en \(I_1\) et \(I_2\) aux deux faces de la lentille sont parallèles.

Le rayon incident \(T_1I_1\) qui, rencontrant en \(I_1\) la face d’entrée, se réfracte suivant \(I_1I_2\), émerge en \(I_2\) parallèlement à sa direction incidente suivant \(I_2T_2\).

En effet, la lentille, se comportant pour ce rayon comme une lame réfringente à faces parallèles qui serait limitée par les plans \(P_1\) et \(P_2\), ne le dévie pas.

La droite \(I_1I_2\) rencontre l’axe en un point O qui est un centre optique. Nous allons vérifier que la position du point O sur l’axe ne dépend pas du point I qui nous a permis de le déterminer. Les triangles semblables \(I_1OC_1\) et \(I_2OC_2\) nous donnent en grandeur et en signe : \[\frac{\overline{OC_1}}{\overline{OC_2}}=\frac{\overline{I_1C_1}}{\overline{I_2C_2}}=\frac{\overline{S_1C_1}}{\overline{S_2C_2}}=\frac{r_1}{r_2}\]

O est donc le point qui partage le segment \(\overline{C_1C_2}\) dans un rapport donné : le rapport des rayons des faces. C’est un point fixe. O est le centre d’homothétie des dioptres et il en résulte qu’il divise également le segment \(S_1S_2\) dans le rapport \(r_1/r_2\). On en conclut que O est plus proche de la face la plus courbe.

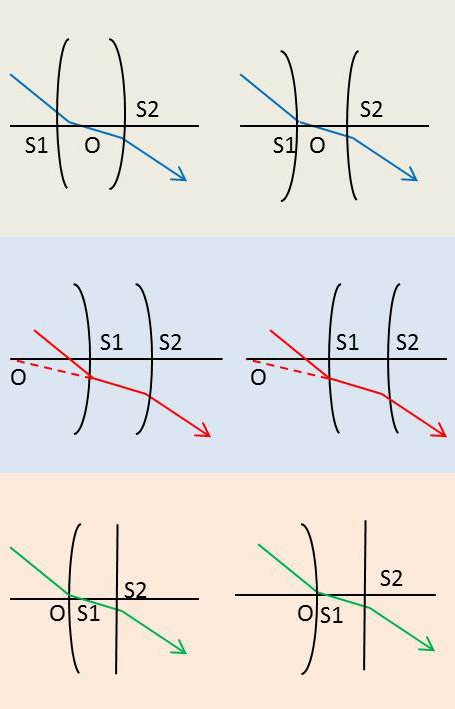Indiquons rapidement les cas possibles :

1. La lentille est biconvexe ou biconcave :

   \(r_1,r_2\) sont de signes contraires.

   Il en est de même des segments \(\overline{OS_1}\) et \(\overline{OS_2}\).

   O est entre \(S_1\) et \(S_2\) donc à l’intérieur de la lentille. Si la lentille est équiconvexe ou équiconcave \(\overline{OS_1}=-\overline{OS_2}\).

   Le point O est situé au milieu de \(\overline{S_1S_2}\) ; c’est le centre de symétrie de la lentille.

2. La lentille est concave convexe :

   \(r_1,r_2\) sont de même signe, les segments \(\overline{OS_1},\overline{OS_2}\) sont aussi de même signe et O est à l’extérieur de la lentille, du côté de la face la plus courbe.

3. La lentille est plan convexe ou plan concave :

   L’un des rayons, \(r_1\) par exemple, est infini.

   Le rapport \(r_1/r_2\) est nul et \(\overline{O_S1}=0\). Le centre optique est alors le sommet de la face courbe.

6. Recherche directe des points principaux

Prolongeons le rayon incident \(T_1I_1\), que nous supposerons cette fois peu incliné sur l’axe, jusqu’à son point de rencontre N avec cet axe.

Soit de même N’ le point où le rayon émergent \(T_2I_2\) rencontre l’axe.

N et N’ sont les points nodaux de la lentille ; ce sont aussi ses points principaux puisque les deux faces de la lentille sont baignées par le même milieu. N a pour conjugué O à travers la face d’entrée ; N’ est le conjugué de O à travers la face de sortie.

Pour trouver les points N et N’, c’est-à-dire les points principaux, il suffira donc :

1. de déterminer le centre optique O ;

2. de chercher le point H de l’axe dont l’image à travers le dioptre \(S_1\) est le point O (on appliquera par exemple à cet effet l’équation de conjugaison du dioptre sphérique rapportée à son sommet), c’est le point principal objet ;

3. de chercher l’image H’ de O à travers le dioptre \(S_2\), c’est à la fois le point nodal image et le point principal image.