Étude de trois réseaux particuliers : le réseau échelette, le réseau échelon de Michelson et le principe des réseaux concaves.

1. Réseau échelette

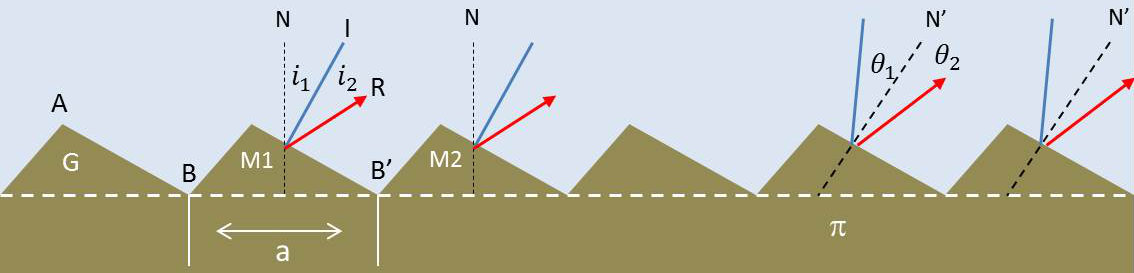Le réseau échelette est un réseau en dent de scie agissant par réflexion.

\(AB\) est une facette du réseau et (\(\pi\)) est le plan du réseau.

Il faut faire attention à la façon de repérer les angles de réfraction et d’incidence. Le repérage peut être effectué de deux manières :

• soit avec \(\overrightarrow{N}~\bot~(\pi)\) : angles \(i_1\) et \(i_2\) ; pas du réseau \(a=BB'\) ;

• soit avec \(\overrightarrow{N'}~\bot~(\pi)\) : angles \(\theta_1\) et \(\theta_2\) ; pas du réseau \(b=AB\).

Dans les deux cas, la différence de marche se calcule en projetant \(M_2\) sur les rayons \(I\) et \(R\) et en écrivant que \(\delta=\overline{HM_1}+\overline{M_1K}\).

Le résultat trouvé dans cet article apparaîtra avec les mêmes conventions, que ce soit avec \(i\) ou avec \(\theta\).

Remarque

Le motif du réseau a une dimension \(b\) appréciable vis à vis du pas \(a\) (problème rencontré quand on ne néglige plus l’épaisseur d’une fente dans un réseau à fente).

L’intensité comportera un terme de diffraction :

\[\begin{aligned} \Phi(u)&=\frac{\sin^2(u)}{u^2}=\operatorname{sinc}^2(u) \\ \text{avec :}\quad u&=\frac{\pi~\delta_1}{\lambda}=\frac{\pi~b}{\lambda}~\{\sin(\theta_2)-\sin(\theta_1)\}\end{aligned}\]

et un terme d’interférence :

\[\begin{aligned} \Psi(\varphi)&=\frac{\sin^2(N~\varphi/2)}{\sin^2(\varphi/2)} \\ \text{avec :}\quad\varphi&=\frac{2\pi~\delta_2}{\lambda}=\frac{2\pi~a}{\lambda}~\{\sin(i_1)+\sin(i_1)\}\end{aligned}\]

On a alors : \[I=I_0~\operatorname{sinc}^2(u)~\frac{\sin^2(N~\varphi/2)}{\sin^2(\varphi/2)}\]

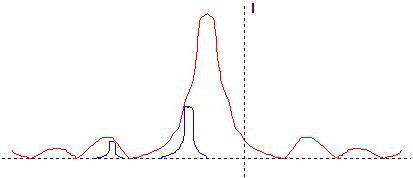On obtient un maximum principal pour \(\delta_1=K_1~\lambda\) pour la diffraction et un maximum pour l’interférence du réseau pour \(\delta_2=K_2~\lambda\), celui-ci étant d’ordre \(K_2\).

Les courbes représentant l’intensité \(I\) (en bleu) sont modulées par la courbe de diffraction (en rouge) exprimée par le premier facteur.

2. Réseau échelon de Michelson

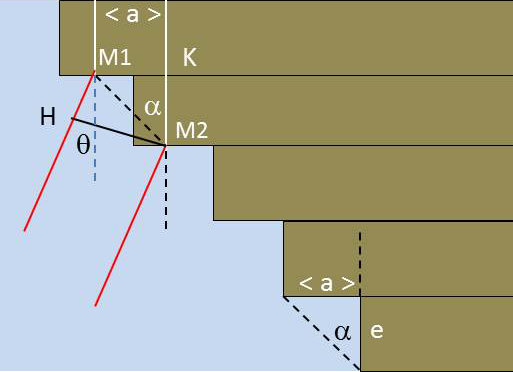Le réseau échelon de Michelson est constitué par un empilement de lames de verre de même épaisseur \(e\).

La différence de marche entre les vibrations diffractées dans la direction \(\theta\) par deux points homologues \(M_1\) et \(M_2\) est donnée par : \[\delta=[KM_2]-[M_1H]=n~e-M_1H\]

On a :

\[\begin{aligned} &M_1H=M_1M_2~\cos(\theta+\alpha)\\ &M_1H=\frac{e}{\cos(\alpha)}~\cos(\theta+\alpha)\\ &M_1H=\frac{e}{\cos(\alpha)}~\{\cos(\alpha)~\cos(\theta)-\sin(\alpha)~\sin(\theta)\}\end{aligned}\]

Par ailleurs : \(\tan(\alpha)=a/e\), ce qui permet d’écrire : \[\delta=n~e~-~e~\big\{\cos(\theta)-\frac{a}{e}~\sin(\theta)\big\}\]

Dans l’approximation des petits angles : \[\sin(\theta)\approx\theta\quad;\quad\cos(\theta)\approx 1\quad;\quad\delta=(n-1)~e+a~\theta\]

Les maximums principaux sont donnés par \(\delta=K~\lambda\) : \[n~e~\{e~\cos(\theta)-a~\sin(\theta)\}=K~\lambda\]

L’ordre d’interférence au centre (\(\theta=0\)) est : \[K_0=\frac{(n-1)~e}{\lambda}\qquad\Rightarrow\qquad K=K_0+\frac{a~\theta}{\lambda}\]

Le centre ne correspond pas généralement à un maximum. La distance entre deux maximums successifs ou séparation angulaire des images de la source dans deux spectres successifs est telle que :

\[\begin{aligned} K&=K_0+\frac{a~\theta_K}{\lambda}\\ K-1&=K_0+\frac{a~\theta_{K-1}}{\lambda}\end{aligned}\]

D’où il vient : \[\theta_K-\theta_{K-1}=\frac{\lambda}{a}\]

On calcule alors la dispersion par différentiation : \[(n-1)~e+a~\theta=K~\lambda\qquad\Rightarrow\qquad\frac{d\theta}{d\lambda}=\frac{K}{a}\]

3. Réseaux concaves

Nous avons déjà vu que, pour rendre les faisceaux incidents parallèles, de même que les faisceaux réfractés, il fallait deux objectifs.

Le procédé du réseau concave permet de se dispenser de la présence de ces deux appareils.

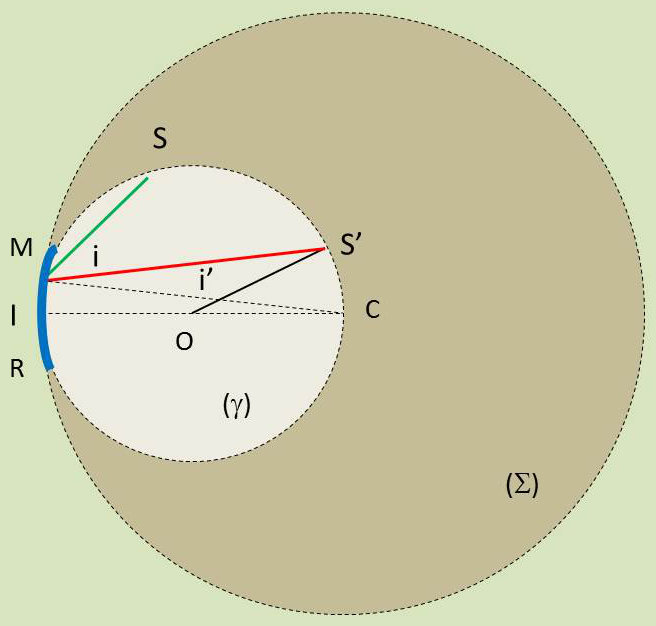
Le réseau R est taillé dans une sphère \(\Sigma\) de centre C.

Le schéma ci-contre représente une coupe horizontale, les traits de R étant verticaux. La source de lumière est \(S\).

Pour que \(S'\) soit maximum principal d’ordre \(K\), il faut que le trajet optique \([SM+MS']\) augmente de \(\delta=K\lambda\) quand on passe d’un trait du réseau au suivant.

Ici, \(CM\) est la normale aux traits du réseau et on a : \[\delta=a~\{\sin(i)+\sin(i')\}=K~\lambda\]

Il faut pour cela deux conditions :

1. \(i=\widehat{SMC}=cte\), donc \(M\in(\gamma)\), cercle passant par \(S, I, C\).

   Ce raisonnement est acceptable parce que la portion de réseau étudiée est très petite et que \((\gamma)\) et \((\Gamma)\) sont tangents en \(I\) mais non ponctuellement.

2. \(i'=\widehat{S'MC}=cte\), donc \(S'\in(\gamma)\).

Ainsi, un point lumineux \(S\in(\gamma)\) donne une série de maximums principaux, tous situés sur \((\gamma)\). Leur position y est définie par les angles \(i\) et \(i'\) de \(IS\) et \(IS'\) avec la normale \(IC\) et liés par la relation : \[\sin(i)+\sin(i')=n~K~\lambda\]

Remarque

En posant \(IC=r\), rayon de courbure du réseau, le rayon du cercle \((\gamma)\) est \(r/2\).

De plus, on voit que \(\widehat{SOS'}=2~i\) comme angle au centre.

Si on fait varier \(i'\) de \(\Delta i'\), on aura donc (pour deux positions voisines de S) : \[S'_1S'_2=\Delta d=\frac{r}{2}~(2~\Delta i')=r~\Delta i'\]

Par différentiation (discrète) de la relation précédente aux sinus: \[\cos(i')~\Delta i'=n~K~\Delta\lambda\]

On obtient finalement : \[\Delta d=r~\frac{n~K~\Delta\lambda}{\cos(i')}\]