1. Considérations générales

Quand un rayon lumineux arrive à la surface de séparation de deux milieux transparent, il se partage en deux rayons : une partie est réfléchie (angle de réflexion égal à l’angle d’incidence) et l’autre est transmise par réfraction suivant les lois de Descartes : \[n_1\sin(i_1)=n_2\sin(i_2)\]

Nous verrons par la suite comment sont établies les formules de Fresnel donnant les coefficients de réflexion et de transmission en amplitude pour une incidence normale : \[r=\frac{n_1-n_2}{n_1+n_2}\quad;\quad t=\frac{2n_1}{n_1+n_2}\]

Dans le cas d’une réflexion air-verre, on a respectivement : \(n_1=1~;~n_2=1,5\). Le coefficient de réflexion est alors négatif et correspond à un déphasage \(\varphi=\pi\) entre l’onde incidente et l’onde réfléchie. Ainsi s’explique la présence de la frange centrale noire dans le miroir de Lloyd.

Le coefficient R de réflexion en énergie est donné par la relation : \[R=r~r^*\quad;\quad R=r^2~~\text{si}~~r\in\mathbb R\]

A et T désignant les coefficients d’absorption et de transmission en énergie : \[R+T+A=1\]

2. Calcul d’une différence de marche

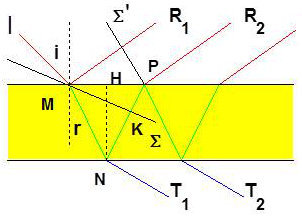On considère qu’il y a des réflexions multiples à l’intérieur de la lame.

Un rayon transmis est noté \(T_i\). Un rayon réfléchi est noté \(R_i\).

Calculons la différence de marche existant entre deux rayons réfléchis successifs, les deux premiers par exemple.

Traçons, à partir de \(M\) et de \(P\), les plans d’onde respectifs \(\Sigma\) et \(\Sigma'\). On sait que ces plans sont perpendiculaires respectivement à \(NP\) au point K du rayon \((R_2)\)et à \((R_1)\) au point \(K'\).

De par la propriété des plans d’onde consécutifs, il y a égalité des chemins optiques : \([IK']=[KP]\).

La différence de marche entre les rayons consécutifs \(R_1\) et \(R_2\) ne sera due qu’au trajet {M,N,K}, c’est-à-dire : \(\delta=[MNK]\).

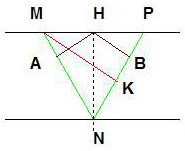Un calcul élémentaire par symétrie montre que le trajet géométrique correspondant est : \[AN+NB=2AN=2HN\cos(r)\]

S’il s’agit d’une lame de verre d’indice \(n\) et d’épaisseur \(e\) plongée dans l’air, cette différence de marche aura pour expression : \[\delta=2n~e~\cos(r)\]

Nous devons par ailleurs tenir compte de la réflexion air-verre en M. Celle-ci entraine pour le rayon \(R_1\) une différence de phase \(\Delta\varphi=\pi\) sur le rayon transmis et par suite sur \(R_2\) lorsque l’incidence est quasi normale. Dans cette hypothèse : \[\Delta\varphi=\frac{2\pi}{\lambda}~\delta'\quad\Rightarrow\quad\delta'=\frac{\lambda}{2}\]

Tout se passe comme si le rayon \(R_2\) avait parcouru en plus le chemin \(\lambda/2\).

D’une façon générale, lorsque les réflexions en \(M\) et \(N\) sont de nature différente, comme c’est ici le cas, on a : \[\Delta=2n~e~\cos(r)+\frac{\lambda}{2}\]

La différence de marche entre \(T_1\) et \(T_2\) vaut \(\delta\), car la réflexion verre-air en P n’entraine pas de déphasage supplémentaire de \(\pi\) .

3. Les interférences

Les rayons \(R_1\) et \(R_2\) peuvent interférer : ils présentent entre eux la différence de marche \(\Delta\).

Ces rayons sont parallèles : les franges sont localisées à l’infini et on peut les observer au foyer d’une lentille visant à l’infini.

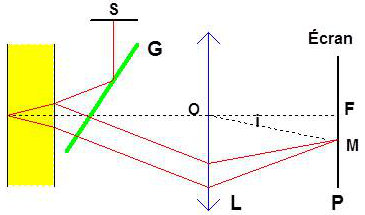
Le dispositif d’observation est schématisé ci-contre. \(G\) est une glace sans tain. L’incidence est supposée quasi normale. La source \(S\) est étendue et la lumière monochromatique.

En chaque point du plan \(P\), donc l’écran, se coupent les rayons ayant traversé la lame sous le même angle \(r\). Leur différence de marche \(\Delta\) établie précédemment ne dépend que de l’inclinaison des rayons et nullement du point \(S\) de la source qui leur a donné naissance.

On va donc observer des anneaux de rayon angulaire \(i\), d’axe \(OF\) et de centre \(F\) (ceci parce que \(L\) est parallèle à la lame).

Le point sera sur un anneau brillant si : \[\Delta=2n~e~\cos(r)+\frac{\lambda}{2}=k~\lambda\]

En faisant \(r=0\), donc \(i=0\) (point F), on obtient \(k_0\) qui est l’ordre d’interférence au centre : \[2n~e+\frac{\lambda}{2}=k_0~\lambda\]

Calculons maintenant le rayon des anneaux avec l’approximation de l’incidence normale qui donne : \[i=n~r\quad;\quad\cos(r)\approx 1-\frac{r^2}{2}=1-\frac{i^2}{2n^2}\]

En revenant à l’expression de \(\Delta\)  : \[2n~e~\big(1-\frac{i^2}{2n^2}\big)+(k_0~\lambda-2n~e)=k~\lambda\]

D’où il vient : \[i^2=\frac{n}{e}~(k_0-k)~\lambda\]

Et le rayon d’ordre \(k\) a pour expression : \[\rho_k=f~i_k=f~\sqrt{\frac{(k_0-k~)n~\lambda}{e}}\qquad f~:\text{ distance focale de }L\]

Si nous supposons \(k_0\) entier, ce qui n’est pas toujours le cas, nous voyons que les rayons croissent comme \(1,~\sqrt{2},~\sqrt{3},~2\dots\).

Remarquons par ailleurs que si \(k_0\) est entier, l’anneau central est brillant, alors que si \(k_0\) est demi-entier, l’anneau central est sombre.

4. Coefficient de réflexion en énergie

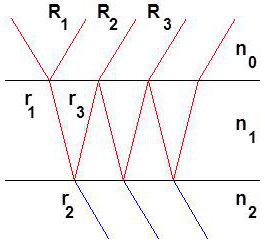Les coefficients de réflexion sur les deux faces sont respectivement :

\[\begin{aligned} &r_1=\frac{n_0-n_1}{n_0+n_1}\qquad\qquad r_2=\frac{n_1-n_2}{n_1+n_2}\\ &r_3=\frac{n_1-n_0}{n_1+n_0}=-r_1\end{aligned}\]

Faisant intervenir les coefficients de réflexion qui contiennent le terme de déphasage supplémentaire, la différence de marche entre deux rayons consécutifs, tels \(R_1\) et \(R_2\), sera : \[\delta=2n~e~\cos(r)\qquad\Rightarrow\qquad\varphi=\frac{2\pi}{\lambda}~\delta\]

Les coefficients de transmission à l’entrée de la lame et à la sortie sont : \[t_1=\frac{2n_0}{n_0+n_1}\quad;\quad t_2=\frac{2n_1}{n_0+n_1}\]

Remarquons que : \[1-r^2=\frac{4n_1n_0}{(n_1+n_0)^2}=t_1.t_2\]

\(A_0\) étant l’amplitude incidente, calculons les amplitudes réfléchies successives :

\[\begin{aligned} &A_1=r_1~A_0 &&=&r_1~A_0\\ &A_2=t_1~r_2~t_2~A_0~\exp(-j\varphi) &&=&(1-r_1^2)~r_2~A_0~\exp(-j\varphi)\\ &A_3=t_1~r_2^2~r_3~t_2~A_0~\exp(-j2\varphi) &&=&-(1-r_1^2)~r_1~r_2^2~A_0~\exp(-j2\varphi)\\ &A_4=t_1~r_2^3~r_3^3~t_2~A_0~\exp(-j3\varphi) &&=&(1-r_1^2)~r_1^2~r_2^3~A_0~\exp(-j3\varphi) \end{aligned}\]

L’amplitude réfléchie est donc : \[A=A_0~\{r_1+(1-r_1^2)~r_2~\exp(-j\varphi)-(1-r_1^2)~r_1~r_2^2~\exp(-j2\varphi)+\dots\}\]

Ce qui peut encore s’écrire : \[A=A_0~\big[r_1+r_2~\exp(-j\varphi)\big]\{1-r_1~r_2~\exp(-j\varphi) +r_1^2~r_2^2~\exp(-j2\varphi)-r_1^3~r_2^3~\exp(-j3\varphi)+\dots\}\]

En définitive : \[A=\frac{r_1+r_2~\exp(-j\varphi)}{1+r_1~r_2~\exp(-j\varphi)}\]

Car on sait que : \[\frac{1}{1+q}=1-q+q^2-q^3+q^4-\dots\qquad (q<1)\]

On a alors : \[AA^*=A_0A_0^*~\frac{[r_1+r_2~\exp(-j\varphi)]~[r_1+r_2~\exp(+j\varphi)]}{[1+r_1~r_2~\exp(-j\varphi)]~[1+r_1~r_2~\exp(+j\varphi)]}\]

D’où : \[R=\frac{AA^*}{A_0A_0^*}=\frac{[r_1+r_2~\exp(-j\varphi)]~[r_1+r_2~\exp(+j\varphi)]}{[1+r_1~r_2~\exp(-j\varphi)]~[1+r_1~r_2~\exp(+j\varphi)]}\]

Avec : \[\varphi=\frac{2\pi}{\lambda}~\delta\qquad (\varphi=\frac{4\pi~n~e}{\lambda}~~\text{en incidence normale})\]

4.1. Étude de la variation de \(R(\varphi)\)

Dérivant la relation précédente, on a : \[\frac{dR}{d\varphi}=\frac{4~r_1~r_2~\sin(\varphi)~(r_1^2+r_2^2-r_1^2~r_2^2-1)}{[1+r_1^2~r_2^2-2~r_1~r_2~\cos(\varphi)]^2}\]

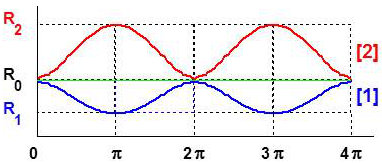Le dénominateur est positif et, en remplaçant les deux coefficients par leurs valeurs en fonction des indices, on obtient, à un facteur constant près \(C > 0\) : \[\frac{dR}{d\varphi}=-C~(n_0-n_1)~(n_1-n_2)~\sin(\varphi)\]

La dérivée est nulle pour \(\varphi=k\pi\) et son signe dépend en fait des valeurs relatives des différents indices.

Courbe [1] : \(n_0<n_1<n_2 \qquad;\qquad\)Courbe [2] : \(n_0<n_1~~;~~n_1>n_2\)

4.2. Couches antiréfléchissantes

En utilisant le fait que: \[\cos(\varphi)=2\cos^2(\varphi/2)-1\]

l’expression \(r_1^2+r_2^2+2~r_1~r_2~\cos(\varphi)\) du dénominateur de R peut être reprise et on peut écrire : \[R=(r_1-r_2)^2+4~r_1~r_2~\cos^2(\varphi/2)\]

La couche sera antireflet si ce coefficient de réflexion est nul, c’est-à-dire si : \[\frac{\varphi}{2}=\frac{\pi}{2}\quad\Rightarrow\quad\varphi=\pi=\frac{4\pi~n_1~e}{\lambda}\quad\Rightarrow\quad e=\frac{\lambda}{4~n_1}\]

Remarque

On ne prend pas la valeur \(\varphi=(2k+1)~\pi\), car il s’agit d’une couche mince (donc \(k=0\) ).

Il faut par ailleurs que \(r_1=r_2\), c’est-a-dire :

\[\frac{n_0-n_1}{n_0+n_1}=\frac{n_1+n_2}{n_1+n_2}\qquad\Rightarrow\qquad\frac{1-n_1/n_0}{1+n_1/n_0}=\frac{1-n_2/n_1}{1+n_2/n_1}\]

On a donc : \[\frac{n_1}{n_0}=\frac{n_2}{n_1}\qquad\Rightarrow\qquad n_1=\sqrt{n_0~n_2}\]

5. Coefficient de transmission en énergie

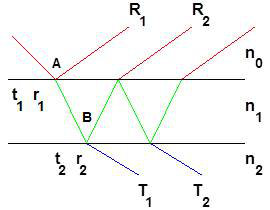En tenant compte de la différence de marche (entre le rayon incident et le premier rayon transmis) due à la traversée de la lame \((AB)\), soit \(\exp(-j\alpha)\), on écrira successivement :

\[\begin{aligned} &A_1=t_1~t_2~A_0\exp(-j\alpha)=a~t_1~t_2\\ &A_2=a~t_1~r_2~r_3~t_2\exp(-j\varphi)\\ &A_3=a~t_1~r_2^2~r_3^2~t_2\exp(-j2\varphi)\end{aligned}\]

En effectuant la sommation : \[A=a~t_1~t_2[1+r_2~r_3~\exp(-j\varphi)+r_2^2~r_3^2~\exp(-j2\varphi)+\dots]\]

Ou encore : \[A=\frac{t_1~t_2~A_0~\exp(-j\alpha)}{1-r_2~r_3~\exp(-j\varphi)}\]

Mais nous savons que : \[t_1~t_2=1-r_1^2\quad;\quad r_3=-r_1\]

On a donc : \[AA^*=\frac{(1-r_1^2)^2~A_0A_0^*}{[1+r_1~r_2~\exp(-j\varphi)]~[1+r_2~r_3~\exp(+j\varphi)]}\]

C’est-à-dire : \[T=\frac{(1-r_1^2)^2}{1+r_1^2~r_2^2+2r_1~r_2\cos(\varphi)}\]

Pour une meilleure compréhension de ce qui suit, on a intérêt à adopter l’écriture contenant pour \(T\) tous les indices : \[T=\frac{(1-r_3^2)^2}{1+r_2^2~r_3^2-2~r_1~r_2\cos(\varphi)}\]

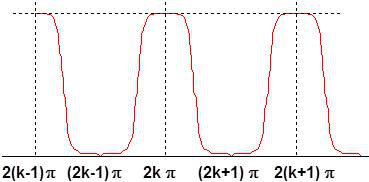Utilisant la relation : \[\cos(\varphi)=1-\sin^2(\varphi/2)\]

Il vient : \[T=\frac{(1-r_3^2)^2}{(1-r_3^2)^2+4~r_2~r_3\sin^2(\varphi/2)}\]

On a donc :

\[\begin{aligned} &T_{max}~:\qquad\frac{\varphi}{2}=k\pi~~\Rightarrow~~\varphi=2k\pi\\ &T_{min}~:\qquad\frac{\varphi}{2}=(2k+1)\frac{\pi}{2}~~\Rightarrow~~\varphi=(2k+1)\pi\end{aligned}\]

5.1. Coefficient de finesse

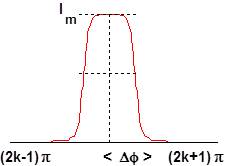Considérons la courbe \(T(\varphi)\). Elle a le même comportement que la courbe représentative de l’intensité \(I(\varphi)\).

Si \(\Delta\varphi\) est l’abscisse qu’il faut parcourir depuis le maximum pour que \(I=I_m/2\), deux minimums étant séparés par une distance de \(2\pi\), on définit le coefficient de finesse par : \[F=\frac{2\pi}{2~\Delta~\varphi}\]

Écrivons que pour : \[\varphi=2k\pi+\Delta\varphi\qquad\big(T=\frac{T_m}{2}\big)\]

on a : \[\sin(\varphi/2)\rightarrow\sin(2k\pi+\Delta\varphi/2)=\pm\sin(\Delta\varphi/2)\approx\pm\Delta\varphi/2\]

On a donc :

\[\begin{aligned} &(1-r_2~r_3)^2+4r_2~r_3(\frac{\Delta\varphi}{2})=2(1-r_2~r_3)^2\\ &\Delta\varphi=\frac{1-r_2~r_3}{\sqrt{r_2~r_3}}\end{aligned}\]

D’où l’expression du coefficient de finesse : \[F=\frac{\pi}{\Delta\varphi}=\frac{\pi\sqrt{r_2~r_3}}{1-r_2~r_3}\]

5.2. Pouvoir de résolution

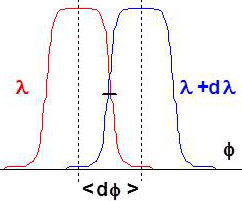On examine les « positions » de deux courbes voisines : \[\varphi=\frac{2\pi\delta}{\lambda}\quad;\quad\varphi=\frac{2\pi~\delta}{\lambda+d\lambda}\]

On a donc : \[d\varphi=2\pi~\delta~\frac{d\lambda}{\lambda^2}\]

Les courbes sont dites séparables lorsqu’elles se coupent à mi-hauteur de leur maximum. On a alors : \[2~\Delta\varphi=d\varphi=\frac{2\pi~\delta}{\lambda}~\frac{d\lambda}{\lambda}\]

Comme on se trouve au voisinage d’un maximum : \[\varphi=\frac{2\pi~\delta}{\lambda}=2k\pi\]

Et comme l’on sait que : \[F=\frac{\pi}{\Delta\varphi}\]

Il s’ensuit que : \[R=\frac{d\lambda}{\lambda}=k~F\]

6. Franges de coin d’air

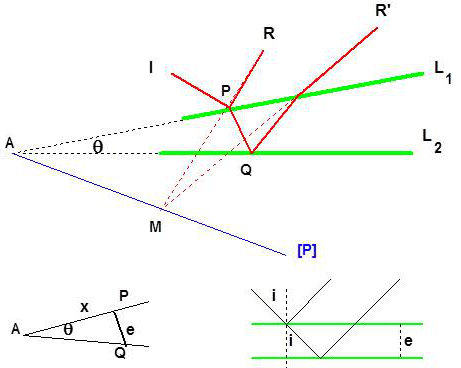Un coin d’air est un système réalisé par deux lames de verre dont les faces en regard se touchent suivant une droite et forment un petit angle \(\theta\).

Les rayons réfléchis \(R\) et \(R'\) se coupent en \(M\). C’est dans le plan formé par l’arête \(A\) et le point \(M\) que sont localisées les franges.

Interfrange : calcul approché

L’angle \(\theta\) étant très petit et les rayons très rapprochés, on considère que \(M\in L1\).

Par ailleurs, le coin d’air peut être assimilé à une lame à faces parallèles dont l’épaisseur au point considéré serait : \[e=x\tan(\theta)\approx x~\theta\]

Les réflexions en \(P\) et \(Q\) sont de natures différentes. La différence de marche est (compte tenu de la très faible épaisseur des lames) : \[\Delta=2~e~\cos(i)+\frac{\lambda}{2}\approx 2~x~\theta\cos(i)+\frac{\lambda}{2}\]

L’interfrange est \(\delta x\) tel que \(d\Delta=\lambda\), c’est à dire : \[\lambda=2~\theta\cos(i)~\delta x\quad\Rightarrow\quad\delta x=\frac{\lambda}{2~\theta\cos(i)}\]

Interfrange : calcul rigoureux

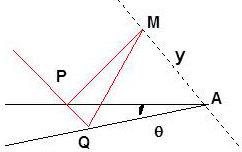Pour un calcul rigoureux, il suffit de rechercher l’interfrange \(\delta y\) dans la surface de localisation.

On a : \[\Delta=2~y~\sin(\theta)+\frac{\lambda}{2}\]

On écrit que : \[d\Delta=\lambda\quad\Rightarrow\quad 2~\sin(\theta)~\delta y=\lambda\]

C’est-à-dire : \[\delta y=\frac{\lambda}{2\sin(\theta)}\]

On notera que l’interfrange est indépendant de l’angle d’incidence \(i\).

Pour déterminer la position des franges noires, on écrira que : \[\Delta=(2k+1)~\frac{\lambda}{2}\]

On a alors :

\[\begin{aligned} 2~x~\theta~\cos(i)&=k\lambda\\ \text{ou bien~:}\qquad 2y~\sin(\theta)&=k\lambda\end{aligned}\]

7. Les anneaux de Newton

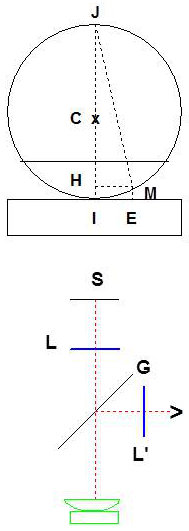Le dispositif pour les produire est constitué par une lentille plan-convexe associée à une lame plate. On est ramené au problème précédent à ceci près que l’on observe des anneaux en raison de la symétrie de révolution du système.

La deuxième figure montre un schéma pratique d’observation (en incidence normale). G est une glace sans tain.

On pose :

\[\begin{aligned} &HM=x\qquad HI=e\\ &HM^2=HI.HJ=e~(2R-e) \quad\Rightarrow\quad x^2\approx 2R~e\end{aligned}\]

La différence de marche est : \[\Delta=2~e~\cos(r)+\frac{\lambda}{2}\]

En incidence normale : \[\cos(r)=1\qquad\Rightarrow\qquad\Delta=2~e+\frac{\lambda}{2}\]

Position des anneaux sombres : \[\Delta=(2k+1)~\frac{\lambda}{2}\qquad\Rightarrow\qquad 2~e=k\lambda\]

Rayon \(x\) des anneaux : \[x_k^2=R~k~\lambda\qquad\Rightarrow\qquad x_k=\sqrt{R~k~\lambda}\]

En opérant en incidence quelconque :

\[\begin{aligned} &\Delta=2~e~\cos(i)+\frac{\lambda}{2}\\ &x_k=\sqrt{\frac{R~k~\lambda}{\cos(i)}}\end{aligned}\]

Au centre, \(x=0\), donc \(k=0\), donc : \[e=\frac{x^2}{2~R}=0\]

On a alors : \[\Delta=\frac{\lambda}{2}\qquad\text{premier anneau sombre}\]

Remarque

Si l’on avait observé le système par transmission, on aurait remarqué des phénomènes complémentaires.