1. Interféromètre de Michelson
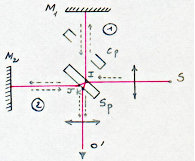Dans l’interféromètre de Michelson, \(S_P\) est une lame de verre à faces parallèles inclinée à \(45^o\) sur les miroirs \(M_1\) et \(M_2\) perpendiculaires et équidistante de ces miroirs.
Le faisceau issu de \(S\) se partage en deux : une partie fait un aller-retour sur \(M_1\) et l’autre sur \(M_2\).
Sur le faisceau [1], on interpose une lame \(C_P\) dite compensatrice, de même nature que \(S_P\) et qui lui est parallèle de sorte que les trajets optiques de [1] et [2] sont identiques.
Ainsi les deux rayons qui vont se retrouver en \(O'\) ne pourront interférer.
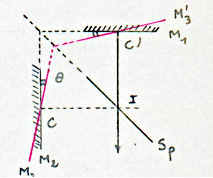Si on fait pivoter \(M_2\) en \(M_3\) autour d’un axe \(C\) perpendiculaire au plan de la figure, de telle sorte que l’angle \(\theta\) soit petit, son image par \(S_P\) qui était \(M_1\) devient \(M'_3\).
Le système étudié devient équivalent à un coin d’air \(\widehat{M_1M_2}\) d’angle \(\theta\).
Sur ce coin d’air, il y a deux réflexions de même nature, mais en \(I\) il y a une réflexion air – verre, de sorte que : \[\delta=2~x~\theta+\frac{\lambda}{2}\]
(\(2\theta\) en raison de l’aller retour dans le coin d’air).
Sur un écran placé en \(O'\), on observe des franges rectilignes parallèles à l’intersection des deux miroirs.
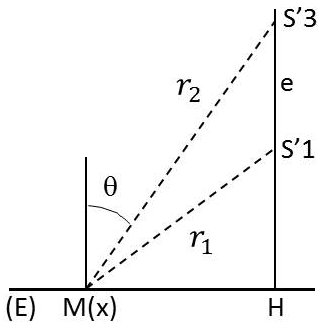Si on déplace \(M_2\) en \(M_3\) parallèlement à \(M_2\) tel que \(M_2M_3 = e\), l’équivalent du système est une lame à faces parallèles \(M_1M'_3\) d’épaisseur \(e\), mais les réflexions sur les deux faces sont de même nature. Étant donnée la symétrie du système de révolution autour de \(IO'\) comme axe. On obtient alors un système d’anneaux dans le plan focal de la lentille.
On pourra, pour étudier ces anneaux, faire un raisonnement différent de celui fait précédemment en imaginant cette fois, comme pour les miroirs de Fresnel, que les images \(S'_1\) et \(S'_3\) de la source \(S\) par rapport à \(M_1\) et \(M'_3\) sont sources secondaires, l’écran d’observation étant perpendiculaire à \(S'_1S'_3\) : \[AA^*=2a^2\Big(1+\cos\frac{2\pi\delta}{\lambda}\Big)\]
Considérant la différence de marche : \[\delta=r_2-r_1\approx l~\cos \theta\approx l~\sqrt{1-\frac{x^2}{L}}\qquad (x\ll L)\]
Il vient : \[AA^*=4a^2\cos^2\frac{\pi l}{\lambda}\Big(1-\frac{x^2}{2L^2}\Big)\]
En lumière monochromatique, on obtient une série d’anneaux brillants et d’anneaux sombres suivant les valeurs de \(x\). Les anneaux sont brillants pour \(A^*A\) maximale : \[\frac{\pi l}{\lambda}\Big(1-\frac{x^2}{2L^2}\Big)=k\pi\]
L’ordre d’interférence au centre est obtenu pour \(x = 0\), c’est-à-dire \(k_0=l/\lambda\) , \(k_0\) n’étant pas forcément entier. On pourra écrire : \[k=k_0~\Big(1-\frac{x^2}{2L^2}\Big)\quad;\quad k_0=\frac{l}{\lambda}\]
Les rayons des anneaux brillants sont donnés par : \[x_k=L~\sqrt{\frac{2(k_0-k)}{k_0}}\]
2. Les miroirs de Jamin
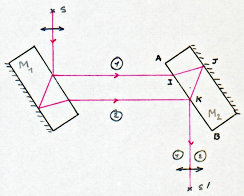Primitivement, les miroirs de Jamin \(M_1\) et \(M_2\) sont rigoureusement parallèles. Les chemins optiques [1] et [2] sont égaux et les rayons n’interfèrent pas en \(S'\). Observons ce qui se passe si on détruit le parallélisme des miroirs en faisant pivoter très légèrement \(M3\) autour de \(AB\).
Le rayon réfléchi en \(K\) tourne d’un petit angle autour d’un axe passant par \(K\). Le trajet \(IJK\) n’est plus dans le plan de la figure et le rayon réfracté de \(JK\) (qui a été déplacé du même angle) est décalé par rapport au premier.
Les deux rayons émergents sont parallèles et on observe au foyer d’une lentille réglée à l’infini des franges d’interférences. Avec cet appareil, les réglages sont difficiles.
3. Interféromètre de Mach-Zender
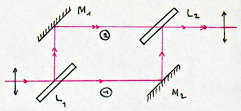Dans l’interféromètre de Mach-Zender, lames et miroirs sont parallèles entre eux. Les rayons [1] et [2] subissent chacun deux réflexions de même nature.
Les chemins optiques [1] et [2] sont égaux de sorte que les rayons émergents n’interfèrent pas.
Il faut créer l’irrégularité à étudier pour avoir des interférences.
4. Interféromètre de Fabry-Perrot
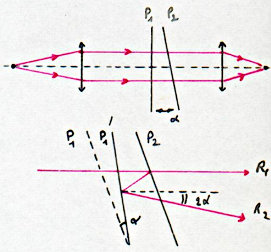L’interféromètre de Fabry-Perrot est basé sur le principe des réflexions multiples. Il est constitué essentiellement par deux lames \(P_1\) et \(P_2\) dont on peut régler l’angle \(\alpha\) (très petit).
Lorsque \(P1\) est parallèle à \(P2\), tous les rayons transmis sont parallèles entre eux. Si \(P_1\) et \(P_2\) forment un petit angle \(a\), les rayons transmis partent en éventail.
On démontre très facilement (comme pour la méthode de Pogendorf) que :
\[\begin{aligned} &(\vec{R}_1,\vec{R}_2)=2\alpha\\ &(\vec{R}_1,\vec{R}_3)=4\alpha\\ &(\vec{R}_1,\vec{R}_n)=(n-1)~2\alpha\end{aligned}\]
Remarque :
Les pouvoirs réflecteurs élevés des faces en regard sont obtenus par évaporation sous vide d’argent ou d’aluminium en couches d’épaisseur convenable. Ces revêtements métalliques ont toutefois l’inconvénient de présenter une certaine absorption \(A = 1-T-R\).
