1. Rappels sur les systèmes différentiels

On suppose connue la méthode de résolution des systèmes différentiels linéaires à coefficient réels constants du type : \[\left\{ \begin{aligned} &F_1(x,~\dot{x},~\ddot{x},~y,~\dot{y},~\ddot{y},~t)=F_1~\exp\{j~(\omega~t+\varphi_1)\}\\ &F_2(x,~\dot{x},~\ddot{x},~y,~\dot{y},~\ddot{y},~t)=F_2~\exp\{j~(\omega~t+\varphi_1)\} \end{aligned} \right.\]

Cas de l’équation sans second membre

On cherche quatre solutions indépendantes de la forme : \[x=X~\exp(\gamma~t)\quad;\quad y=Y~\exp(\gamma~t)\]

La solution générale est de la forme : \[x=\sum_{i=1}^4 C_i~X_i~\exp(\gamma_i~t)\quad;\quad y=\sum_{i=1}^4 C_i~Y_i~\exp(\gamma_i~t)\]

Cas de l’équation avec second membre

On cherche une solution particulière de la forme : \[x=X~\exp(j~\omega~t)\quad;\quad y=Y~\exp(j~\omega~t)\]

La solution générale est de la forme : \[\left\{ \begin{aligned} x=\sum_{i=1}^4 C_i~X_i~\exp(\gamma_i~t)+X~\exp(j~\omega~t)\\ y=\sum_{i=1}^4 C_i~Y_i~\exp(\gamma_i~t)+Y~\exp(j~\omega~t) \end{aligned} \right.\]

2. Oscillations libres en absence de frottements

2.1. Couplage par élasticité

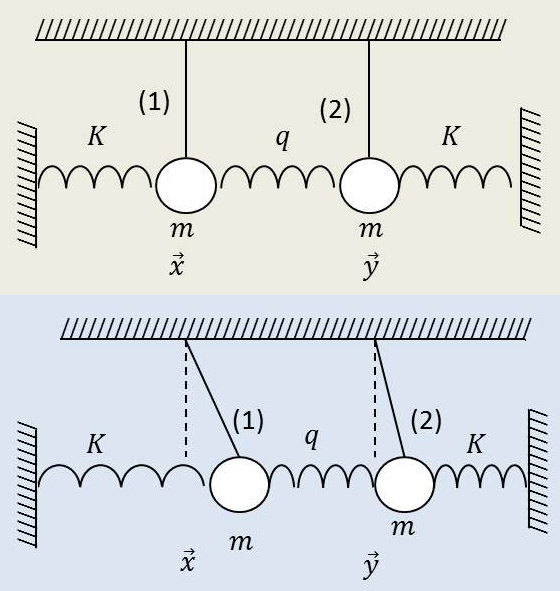Deux pendules de même masse \(m\) sont couplés par un système de ressorts de raideurs \(k,~q\) comme indiqué sur la figure ci-contre.

Les fils qui soutiennent les pendules étant très longs (ce que le dessin ne met pas en évidence, on peut considérer que le mouvement a lieu suivant une horizontale.

Dans ces conditions, \(x,~y\) représentent les élongations respectives des pendules (1) et (2).

L’équilibre des forces se traduit par les relations :

Pendule (1) : \[m~\frac{d^2x}{dt^2}=-k~x+q~(y-x)\]

Pendule (2) : \[m~\frac{d^2y}{dt^2}=-k~y+q~(y-x)\]

Ce qui conduit au système d’équations : \[[1]\qquad \left\{ \begin{aligned} &m~\frac{d^2x}{dt^2}+(k+q)~x-q~y=0\\ &m~\frac{d^2y}{dt^2}+(k+q)~y-q~x=0 \end{aligned} \right.\]

Appliquons la méthode générale de résolution de tels systèmes et cherchons un système de solutions de la forme : \[x=X~\exp(\gamma~t)\quad;\quad y=Y~\exp(\gamma~t)\]

En remplaçant \(x,~y\) par leurs valeurs dans le système [I] et en simplifiant par \(\exp(\gamma~t)\) : \[\left\{ \begin{aligned} &(m~\gamma^2+k+q)~X-q~Y=0\\ &(m~\gamma^2+k+q)~Y-q~X=0 \end{aligned} \right.\]

Il n’y aura de solutions non nulles que si le déterminant des coefficients est nul, c’est-à-dire : \[(m~\gamma^2+k+q)^2-q^2=0\]

Il y a alors deux solutions : \[m~\gamma^2+k+q=\pm q\qquad\Rightarrow\qquad \gamma^2=-\frac{k}{m}\quad\text{et}\quad\frac{k+2~q}{m}\]

On pose : \[\omega'=\sqrt{\frac{k}{m}}\quad;\quad \omega"=\sqrt{\frac{k+2~q}{m}}\]

D’où les 4 valeurs de \(\gamma\) : \[\gamma_{1,2}=\pm j~\omega'\quad;\quad \gamma_{3,4}=\pm j~\omega''\]

Pour le rapport : \[\frac{Y}{X}=\frac{m~\gamma^2+k+q}{q}\]

On aura : \[\gamma=\pm j~\omega'~~\Rightarrow~~\frac{Y}{X}=1\quad;\quad \gamma=\pm j~\omega''~~\Rightarrow~~\frac{Y}{X}=-1\]

On peut poser arbitrairement \(X = 1\). Les 4 solutions particulières sont alors : \[[1]\quad \left\{ \begin{aligned} &x=\exp(j~\omega'~t)\\ &y=\exp(j~\omega'~t) \end{aligned} \right. \qquad [2]\quad \left\{ \begin{aligned} &x=\exp(-j~\omega'~t)\\ &y=\exp(-j~\omega'~t) \end{aligned} \right.\]

\[[3]\quad \left\{ \begin{aligned} &x=\exp(j~\omega'~t)\\ &y=\exp(-j~\omega'~t) \end{aligned} \right. \qquad [4]\quad \left\{ \begin{aligned} &x=\exp(j~\omega'~t)\\ &y=\exp(-j~\omega'~t) \end{aligned} \right.\]

La solution générale est une combinaison linéaire de ces 4 solutions. On peut écrire : \[\left\{\begin{aligned} x=C_1\exp(j~\omega'~t)+C_2~\exp(-j~\omega'~t)+C_3~\exp(j~\omega''~t)+C_4~\exp(-j~\omega''~t)\\ y=C_1\exp(j~\omega'~t)+C_2~\exp(-j~\omega'~t)-C_3~\exp(j~\omega''~t)-C_4~\exp(-j~\omega''~t) \end{aligned} \right.\]

Les constantes sont arbitraires ; on doit les déterminer à partir des vitesses et des élongations initiales.

Nous allons voir qu’un choix convenable de ces conditions initiales permet d’obtenir l’un ou l’autre de deux mouvements sinusoïdaux dits mouvements principaux.

Premier mouvement principal

Pour \(t=0\) : \[[1]\quad x=y=a\quad \left\{ \begin{aligned} &C_1+C_2+C_3+C_4=a\\ &C_1+C_2-C_3-C_4=a \end{aligned} \right. \qquad \left\{ \begin{aligned} &C_1+C_2=a\\ &C_3+C_4=0 \end{aligned} \right.\]

\[[2]\quad\frac{dx}{dt}=\frac{dy}{dt}=0\quad \left\{ \begin{aligned} &j\omega'(C_1+C_2)+j\omega''(C_3-C_4)=0\\ &j\omega'(C_1-C_2)-j\omega''(C_3-C_4)=0 \end{aligned} \right. \qquad \left\{ \begin{aligned} &C_1-C_2=0\\ &C_3-C_4=a \end{aligned} \right.\]

En définitive : \[C_1=C_2=\frac{a}{2}\qquad;\qquad C_3=C_4=0\]

Le mouvement s’écrira : \[\left\{ \begin{aligned} &x=\frac{a}{2}~\{\exp(j~\omega'~t)+\exp(-j~\omega'~t)\}=a~\cos\omega'~t\\ &y=\frac{a}{2}~\{\exp(j~\omega'~t)+\exp(-j~\omega'~t)\}=a~\cos\omega'~t \end{aligned} \right.\]

Nous avons deux mouvements sinusoïdaux synchrones en phase. Ceci pouvait se prévoir par la simple considération des conditions initiales. Chacun des pendules oscille indépendamment et le ressort de couplage, gardant une longueur constante, ne joue aucun rôle.

Deuxième mouvement principal

Cette fois, les conditions initiales sont : \[x=a\quad;\quad y=-a\quad;\quad \frac{dx}{dt}=\frac{dy}{dt}=0\]

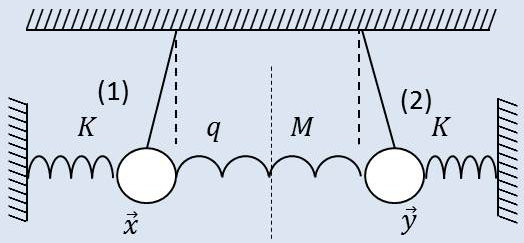On voit tout de suite que le milieu \(M\) du ressort \(q\) est fixe. Chacun des pendules peut être considéré comme subissant seul les raideurs \(k\) et \(2~q\).

Nous trouverons donc des oscillations en opposition de phase de pulsation \[\omega''=\sqrt{\frac{k+2~q}{m}}\]

Les conditions initiales exigent en effet : \[\left\{ \begin{aligned} &C_1+C_2+C_3+C_4=a\\ &C_1+C_2-C_3-C_4=-a \end{aligned} \right. \quad\text{d'où}\quad \left\{ \begin{aligned} &C_1+C_2=0\\ &C_3+C_4=a \end{aligned} \right.\]

\[\left\{ \begin{aligned} &j~\omega'~(C_1-C_2)+j~\omega''~(C_3-C_4)=0\\ &j~\omega'~(C_1-C_2)-j~\omega''~(C_3-C_4)=0 \end{aligned} \right.\]

En définitive : \[C_1=C_2=0\quad;\quad C_3=C_4=\frac{a}{2}\]

L’équation du mouvement s’écrit : \[\left\{ \begin{aligned} &x=\frac{a}{2}~\{\exp(j~\omega''~t)+\exp(-j~\omega''~t)\}\\ &y=-\frac{a}{2}~\{\exp(j~\omega''~t)+\exp(-j~\omega''~t)\} \end{aligned} \right. \quad\text{ou encore}\quad \left\{ \begin{aligned} &x=a~\cos\omega''~t\\ &y=-a~\cos\omega''~t \end{aligned} \right.\]

Les mouvements sont en opposition de phase et la pulsation de chacun d’eux est bien : \[\omega''=\sqrt{\frac{k+2~q}{m}}\]

On remarque que la composition des résultats trouvés pour ces deux mouvements principaux pourra donner une solution générale du système différentiel. On l’écrira sous la forme : \[\left\{ \begin{aligned} &x=a~\cos(\omega'~t+\varphi_1)+b~\cos(\omega''~t+\varphi_2)\\ &y=a~\cos(\omega'~t+\varphi_1)-b~\cos(\omega''~t+\varphi_2) \end{aligned} \right.\]

Conditions initiales quelconques

Dans le cas de conditions initiales quelconques, on observe en général un phénomène de battements. Ceci se produit par exemple pour les conditions initiales suivantes : \[t=0\quad;\quad x=a\quad;\quad y=0\quad;\quad \frac{dx}{dt}=\frac{dy}{dt}=0\]

On obtient alors : \[\left\{ \begin{aligned} &C_1+C_2+C_3+C_4=a\\ &C_1+C_2-C_3-C_4=0 \end{aligned} \right. \qquad \left\{ \begin{aligned} j\omega'~(C_1-C_2)+j~\omega''~(C_3-C_4)=0\\ j\omega'~(C_1-C_2)-j~\omega''~(C_3-C_4)=0 \end{aligned} \right.\]

Ce qui conduit à :

\[\begin{aligned} C_1+C_2=\frac{a}{2}\qquad&;\qquad C_3+C_4=\frac{a}{2}\\ C_1-C_2=0\qquad&;\qquad C_3-C_4=0\end{aligned}\]

D’où : \[C_1=C_2=C_3=C_4=0\]

Les solutions sont alors : \[\left\{ \begin{aligned} x=\frac{a}{2}~\Big\{\frac{\exp(j~\omega'~t)+\exp(-j~\omega'~t)}{2}+\frac{\exp(j~\omega''~t)+\exp(-j~\omega''~t)}{2}\Big\}\\ y=\frac{a}{2}~\Big\{\frac{\exp(j~\omega'~t)+\exp(-j~\omega'~t)}{2}-\frac{\exp(j~\omega''~t)+\exp(-j~\omega''~t)}{2}\Big\} \end{aligned} \right.\]

Ou encore : \[\left\{ \begin{aligned} &x=\frac{a}{2}~(\cos\omega'~t+\cos\omega''~t)\\ &y=\frac{a}{2}~(\cos\omega'~t-\cos\omega''~t) \end{aligned} \right. \quad\text{càd.~:}\quad \left\{ \begin{aligned} &x=a~\cos\frac{(\omega'+\omega'')~t}{2}~\cos\frac{(\omega'-\omega'')~t}{2}\\ &y=a~\sin\frac{(\omega'+\omega'')~t}{2}~\sin\frac{(\omega'-\omega'')~t}{2} \end{aligned} \right.\]

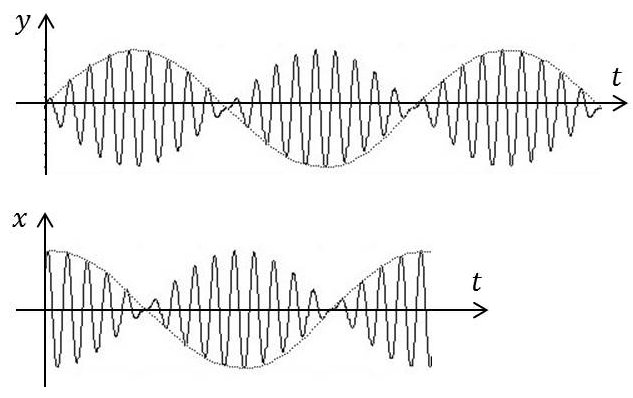On obtient deux mouvements sinusoïdaux dont les amplitudes sont modulées avec les pulsations : \[\frac{\omega'-\omega''}{2}\]

On observe des battements : l’un des pendules oscille avec la maximum d’amplitude alors que l’autre est arrêté, et inversement.

Les amplitudes varient en quadrature. On a constamment échange d’énergie de l’un à l’autre pendule. De plus, les mouvements sont eux même en quadrature.

2.2. Coefficient de couplage

Revenons à l’équation aux pulsations propres : \[(m\gamma^2+k+q)^2-q^2=0\]

Nous avons vu qu’il y a quatre solutions pour \(\gamma\). Écrivons cette relation sous la forme : \[\Big(\frac{m~\gamma^2}{k+q}+1\Big)^2-\Big(\frac{q}{k+q}\Big)^2=0\]

On pose : \[\omega^2=\frac{k+q}{m}\]

\(\omega\) : pulsation d’un pendule, l’autre étant bloqué (ou pulsation du pendule non couplé, mais non isolé)

On pose : \[K=\frac{q}{k+q}\quad;\quad 0\leq K\leq 1\qquad\text{K coefficient de couplage}\]

Deux cas de couplage :

\[\begin{aligned} &q\leq k\qquad K\rightarrow 0\qquad\text{couplage lâche}\\ &k\leq q\qquad K\rightarrow 1\qquad\text{couplage serré}\end{aligned}\]

L’équation aux pulsations propres peut s’écrire : \[\frac{\gamma^2}{\omega^2}+1=\pm K \quad\Rightarrow\quad \left\{ \begin{aligned} -\frac{\gamma_1^2}{\omega^2}=1-K\\ -\frac{\gamma_2^2}{\omega^2}=1+K \end{aligned} \right.\]

Or, on sait que : \[\gamma_1^2=-\omega'^2\quad;\quad \gamma_2^2=-\omega''^2\]

On a donc : \[-\frac{\omega'^2}{\omega^2}=1-K\quad;\quad \frac{\omega''^2}{\omega^2}=1-K\]

Les écarts de pulsation sont liés au coefficient de couplage. On le voit bien en considérant le cas suivant :

\[\begin{aligned} &K=0\qquad\omega'=\omega''=\omega\qquad\qquad\quad\text{couplage lâche}\\ &K=1\qquad\frac{\omega'}{\omega}=0~~;~~\frac{\omega''}{\omega}=\sqrt{2}\qquad\text{couplage serré}\end{aligned}\]

2.3. Analogie électrique

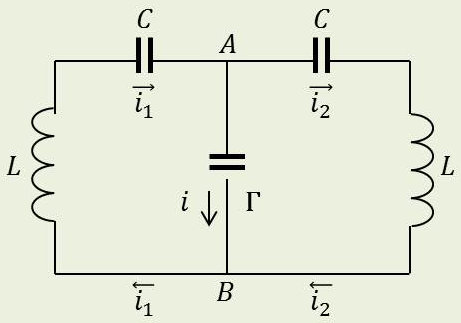\(k\rightarrow 1/C\) : Ressort équivalence capacité

\(m\rightarrow L\) : Masse équivalence self

\(f\rightarrow R\) : Résistance équivalence frottement visqueux

L’analogie électrique sera donc représentée par le schéma ci-contre. Les deux circuits oscillants ont en commun une capacité \(\Gamma\).

Équations du circuit :

\[\begin{aligned} &V_A-V_B=\frac{1}{\Gamma}\int i~dt=-L~\frac{di_1}{dt}-\frac{1}{C}\int i_1~dt\\ &V_A-V_B=\frac{1}{\Gamma}\int i~dt=+L~\frac{di_2}{dt}-\frac{1}{C}\int i_2~dt\end{aligned}\]

On a de plus : \[i=i_1-i_2\quad;\quad i_1=\frac{dq_1}{dt}\quad;\quad i_2=\frac{dq_2}{dt}\]

On obtient : \[\left\{ \begin{aligned} L~\frac{d^2q_1}{dt^2}+\Big(\frac{1}{\Gamma}+\frac{1}{C}\Big)~q_1-\frac{1}{\Gamma}~q_2=0\\ L~\frac{d^2q_2}{dt^2}+\Big(\frac{1}{\Gamma}+\frac{1}{C}\Big)~q_2-\frac{1}{\Gamma}~q_1=0 \end{aligned} \right.\]

Coefficient de couplage : \[K=\frac{1/\Gamma}{(1/\Gamma)+(1/C)}\]

Nous avons bien des équations analogues à celles du cas mécanique. On trouvera deux pulsations principales (\(\omega'~,~\omega''\)).

Conditions initiales 1

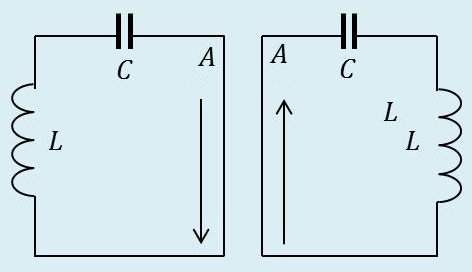\(\Gamma\) est déchargée.

\(C_1,~C_2\) également chargées.

Aucun courant ne passe dans \(\Gamma\). Tout se passe comme si l’on avait deux circuits séparés. On ferme les circuits en A. La pulsation est : \[\omega'=\frac{1}{\sqrt{L~C}}\]

Conditions initiales 2

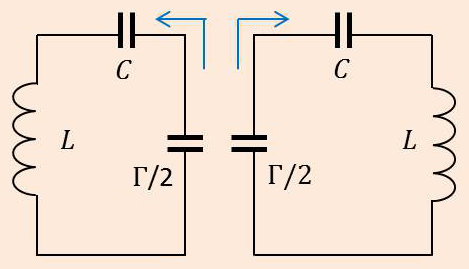On charge \(\Gamma\), puis on la décharge dans (1) et (2) en fermant les deux circuits en A. Le courant issu de \(\Gamma\) se partage également dans les deux circuits.

Tout se passe comme si l’on avait un circuit avec des capacités \(C\) et \(\Gamma/2\) en série, soit une capacité \(C'\) donnée par la relation : \[\frac{1}{C'}=\frac{1}{C}+\frac{1}{\Gamma/2}\quad\Rightarrow\quad C'=\frac{\Gamma~C}{\Gamma+2~C}\]

La pulsation dans chaque circuit est alors : \[\omega''=\frac{1}{\sqrt{\cfrac{L~\Gamma~C}{\Gamma+2~C}}}=\sqrt{\frac{\Gamma+2~C}{L~\Gamma~C}}\]

3. Couplage par inertie

3.1. Cas mécanique

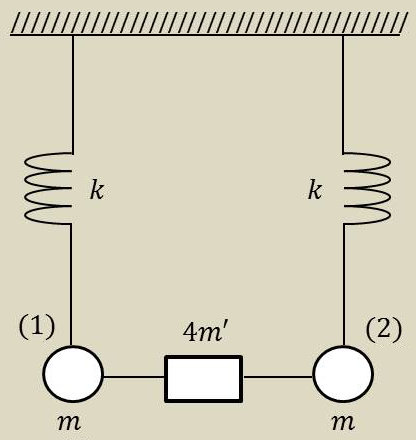Considérons le montage constitué par deux pendules identiques (1) et (2) rappelés par des ressorts de raideur \(k\).

Ils sont reliés par une tige rigide qui a une masse négligeable. Elle porte en son centre une masse \(4~m'\), la masse des pendules étant \(m\).

Nous ne tiendrons compte que des frottements d’inertie de translation des masses et des forces de rappel des ressorts.

La force d’inertie \(m\cfrac{d^2x}{dt^2}\) équilibre :

• la force de rappel du ressort : \(-kx\) équilibre :;

• la moitié de la force de réaction de la masse \(4~m'\) additionnelle : \(2~m'~\cfrac{d^2z}{dt^2}\) (bras de levier divisant par 2 la réaction).

\[\begin{aligned} m~\frac{d^2x}{dt^2}&=-k~x+2~m'~\frac{d^2z}{dt^2}\quad;\quad z=\frac{x+y}{2}\\ \frac{d^2z}{dt^2}&=\frac{1}{2}~\Big(\frac{d^2x}{dt^2}+\frac{d^2y}{dt^2}\Big)\end{aligned}\]

On trouvera alors : \[\left\{ \begin{aligned} &(m+m')~\frac{d^2x}{dt^2}+k~x+m~\frac{d^2y}{dt^2}=0\\ &(m+m')~\frac{d^2y}{dt^2}+k~y+m'~\frac{d^2x}{dt^2}=0 \end{aligned} \right.\]

Soit un système de solutions de la forme : \[x=X~\exp(\gamma~t)\quad;\quad y=Y~\exp(\gamma~t)\]

Simplifions par \(\exp(\gamma~t)\). On a : \[\left\{ \begin{aligned} X~(m+m')~\gamma^2+Y~m'~\gamma^2=0\\ Y~(m+m')~\gamma^2+X~m'~\gamma^2=0 \end{aligned} \right.\]

Le déterminant doit être nul : \[\{(m+m')~\gamma^2+k\}^2-m'^2~\gamma^4=0\]

On a donc : \[\left\{ \begin{aligned} &(m+m')~\gamma^2+k=m'~\gamma^2\\ &(m+m')~\gamma^2+k=-m'~\gamma^2 \end{aligned} \right. \qquad\text{soit :}\quad \left\{ \begin{aligned} &\gamma_1^2=-\frac{k}{m}=(j~\omega')^2\\ &\gamma_2^2=-\frac{k}{m+2~m'}=(j~\omega'')^2 \end{aligned} \right.\]

Ce qui donne quatre solutions : \[\omega'=\sqrt{\frac{k}{m}} \qquad\qquad \left\{ \begin{aligned} &\gamma_1=+j~\omega'\\ &\gamma'_1=-j~\omega' \end{aligned} \right.\]

\[\omega''=\sqrt{\frac{k}{m+2~m'}} \quad\quad \left\{ \begin{aligned} &\gamma_2=+j~\omega''\\ &\gamma'_2=-j~\omega'' \end{aligned} \right.\]

Le mouvement général sera alors de la forme : \[\left\{ \begin{aligned} &x=a~\cos(\omega'~t+\varphi_1)+b~\cos(\omega''~t+\varphi_2)\\ &y=-a~\cos(\omega'~t+\varphi_1)+b~\cos(\omega''~t+\varphi_2) \end{aligned} \right. \qquad\text{car :}\quad \left\{ \begin{aligned} &\gamma_1~~\text{ou}~~\omega'~:~\frac{Y}{X}=-1\\ &\gamma_2~~\text{ou}~~\omega"~:~\frac{Y}{X}=+1 \end{aligned} \right.\]

On définit un coefficient de couplage : \[K\neq k\quad;\quad K=\frac{m'}{m+m'}\]

Soit la pulsation des pendules non couplés (pulsation de l’un lorsque l’autre est bloqué à sa position d’équilibre) : \[\omega=\sqrt{\frac{k}{m+m'}}\]

On peut écrire :

\[\begin{aligned} &\frac{\omega^2}{\omega'^2}=\frac{k}{m+m'}~\frac{m}{k}=\frac{m}{m+m'}\\ &\frac{\omega^2}{\omega'^2}=1-\frac{m'}{m+m'}=1-K=\frac{T'^2}{T^2}\end{aligned}\]

Si \(K\rightarrow 0\) (couplage lâche), \(T'\rightarrow T\) : la période du pendule non couplé se confond avec celle du pendule isolé.

\[\begin{aligned} &\frac{\omega^2}{\omega''^2}=\frac{k}{m+m'}~\frac{m+2~m'}{k}=\frac{m+2~m'}{m+m'}\\ &\frac{\omega^2}{\omega''^2}=1+K=\frac{T''^2}{T^2}\end{aligned}\]

Comme dans le chapitre précédent, nous pouvons étudier le mouvement grâce aux conditions initiales. Les résultats sont :

Cas 1 : \(\quad x=a\quad;\quad y=a\quad;\quad v_x=v_y=0 \)

Oscillateurs en phase : \[\omega_1=\omega''=\sqrt{\frac{k}{m+2~m'}}\]

Tout se passe comme si un ressort de raideur \(2~k\) s’appliquait à la masse (\(2~m+4~m'\)).

Cas 2 : \(\quad x=a\quad;\quad y=-a\quad;\quad v_x=v_y=0\)

La masse reste au repos. Tout se passe comme si elle n’existait pas ; les deux pendules vont osciller en opposition de phase avec la pulsation : \[\omega_2=\omega'=\sqrt{\frac{k}{m}}\]

3.2. Analogie électrique

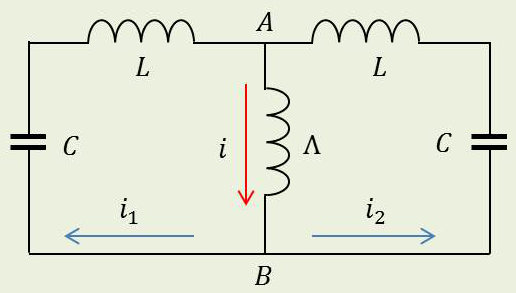L’analogie électrique consistera en deux circuits couplés par une self.

\[\begin{aligned} &V_A-V_B=\Lambda~\frac{di}{dt}=-\frac{1}{C}\int i_1~dt-L~\frac{di_1}{dt}\\ &V_A-V_B=\Lambda~\frac{di}{dt}=-\frac{1}{C}\int i_2~dt-L~\frac{di_2}{dt}\end{aligned}\]

Le sens du courant est défini de façon à correspondre au sens dans le montage précédent :

\[\begin{aligned} &i=i_1+i_2\quad;\quad\frac{dq_1}{dt}=i_1\quad;\quad\frac{dq_2}{dt}=i_2\\ &L~\frac{d^2q}{dt^2}+\Lambda~\Big(\frac{d^2q_1}{dt^2}+\frac{d^2q_2}{dt^2}\Big)+\frac{1}{C}~q_1=0\end{aligned}\]

Il s’ensuit que : \[\left\{ \begin{aligned} &(L+\Lambda)~\frac{d^2q_1}{dt^2}+\frac{q_1}{C}+\Lambda~\frac{d^2q_2}{dt^2}=0\\ &(L+\Lambda)~\frac{d^2q_2}{dt^2}+\frac{q_2}{C}+\Lambda~\frac{d^2q_1}{dt^2}=0 \end{aligned} \right. \qquad K=\frac{\Lambda}{L+\Lambda}\]

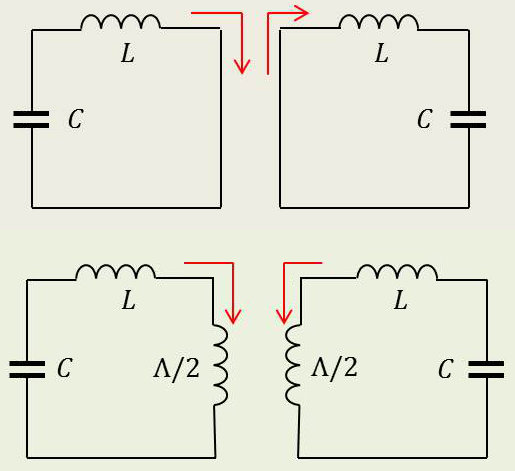Nous obtenons un système analogue. On retrouverait là encore deux pulsations principales :

– Une pulsation équivalente au circuit [1] : \[\omega'=\sqrt{\frac{1}{L~C}}\]

– Une pulsation équivalente au circuit [2] : \[\omega''=\sqrt{\frac{1}{\Big(L+\cfrac{\Lambda}{2}\Big)~C}}\]

On notera que \(\cfrac{\Lambda}{2}\) correspond à \(\cfrac{4~m'}{2}\).

4. Oscillateurs non identiques

Pour simplifier le problème, nous allons prendre le cas des pendules couplés par élasticité, où seuls les ressorts extrêmes \(k\) n’auront pas la même raideur.

Nous utiliserons pour la mise en équation la même méthode que précédemment. Nous obtenons le système différentiel : \[\left\{ \begin{aligned} &m~\frac{d^2x}{dt^2}+(k+q)~x-q~y=0\\ &m~\frac{d^2y}{dt^2}+(k+q)~y-q~x=0 \end{aligned} \right.\]

avec une solution de la forme : \[X=\exp(\gamma~t)\quad;\quad Y=\exp(\gamma~t)\]

On retrouve : \[\left\{ \begin{aligned} &(m~\gamma^2+k_1+q)~X-q~Y=0\\ &(m~\gamma^2+k_2+q)~Y-q~X=0 \end{aligned} \right.\]

\[\Delta=(m~\gamma^2+k_1+q)~(m~\gamma^2+k_2+q)-q^2=0\]

Coefficient de couplage : \[K=\sqrt{\frac{q^2}{(k_1+q)(k_2+q)}}\]

Pulsations :

\[\begin{aligned} &\omega_1=\sqrt{\frac{k_1+q}{m}}\quad;\quad \omega_2=\sqrt{\frac{k_2+q}{m}}\\ &\omega_2>\omega_1\quad;\quad K~\omega_1~\omega_2=\frac{q}{m}\end{aligned}\]

Écrivons l’expression de \(\Delta\) sous la forme :

\[\begin{aligned} &(\gamma^2+\omega_1^2)~(\gamma^2+\omega_2^2)-\frac{q^2}{m^2}=0\quad;\quad\omega^2=-\gamma^2\\ &(\omega_1^2-\omega^2)~(\omega_2^2-\omega^2)-K^2~\omega_1^2~\omega_2^2=0\end{aligned}\]

Désignons par \(T\) le premier membre (trinôme du second degré en \(\omega^2\). Plusieurs cas peuvent se produire : \[\begin{array}{lll} \omega=0\quad &T=\omega_1^2~\omega_2^2~(1-K^2)\quad &T>0\quad\text{car :}~~0\leq K\leq 1\\ \omega=\omega_1 &T=-K~\omega_1^2~\omega_2^2 &T<0\\ \omega=\omega_2 &T=-K~\omega_1^2~\omega_2^2 &T>0\\ \omega\rightarrow\infty\quad &T\rightarrow 0 \end{array}\]

Toujours deux racines réelles en \(\omega^2\) : \[\omega^2=\omega'^2\quad;\quad \omega^2=\omega''^2\]

Elles sont situées dans cet ordre : \[0<\omega'<\omega_1<\omega_2<\omega''<+\infty\]

Tous calculs faits, on obtient :

\[\begin{aligned} &\omega'^2=\frac{\omega_1^2+\omega_2^2}{2}-\sqrt{(\frac{\omega_2^2-\omega_1^2}{2}\Big)^2+K^2~\omega_1^2~\omega_2^2}\\ &\omega''^2=\frac{\omega_1^2+\omega_2^2}{2}+\sqrt{\Big(\frac{\omega_2^2-\omega_1^2}{2}\Big)^2+K^2~\omega_1^2~\omega_2^2}\end{aligned}\]

Ces résultats montrent que \(\omega'\) diminue toujours lorsque \(K\) croît de zéro à 1, tandis que \(\omega''\) décroît.

Couplage très lâche \((K\approx 0)\)

Pour \(K=0\), on a \(\omega'^2=\omega_1^2\) et \(\omega''^2=\omega_2^2\).

Les périodes propres sont celles des deux oscillateurs pris isolément.

Couplage lâche

\(K\), sans être nul, est assez petit pour que l’on puisse admettre que : \[K~\omega_1~\omega_2\ll\omega_1^2-\omega_2^2\]

On négligera par ailleurs les termes en \(K^4\) de sorte que  : \[\omega'^2=\omega_1^2~\Big\{1-\frac{K^2~\omega_2^2}{\omega_2^2-\omega_1^2}\Big\}\quad;\quad \omega''^2=\omega_2^2~\Big\{1-\frac{K^2~\omega_1^2}{\omega_2^2-\omega_1^2}\Big\}\]

Deux constatations : \[\begin{array}{llll} \cfrac{Y}{X}=\frac{\omega_1^2-\omega^2}{K~\omega_1~\omega_2}\qquad &\text{Si}~\omega\rightarrow\omega', &\cfrac{Y}{X}\approx\cfrac{K~\omega_1~\omega_2}{\omega_2^2-\omega_1^2}\rightarrow 0~: &\text{X oscille seul }\\ \cfrac{X}{Y}=\frac{\omega_2^2-\omega^2}{K~\omega_1~\omega_2} &\text{Si}~\omega\rightarrow\omega'', &\cfrac{X}{Y}\approx\cfrac{K\omega_1~\omega_2}{\omega_2^2-\omega_1^2}\rightarrow 0~:\quad &\text{Y oscille seul } \end{array}\]

5. Oscillations forcées des oscillateurs couplés

On suppose maintenant que le système couplé est attaqué par une force extérieure sinusoïdale. Nous désignerons sous le nom de primaire l’oscillateur qui reçoit directement la force extérieure, et sous le nom de secondaire l’autre oscillateur qui ne subit que les réactions du primaire.

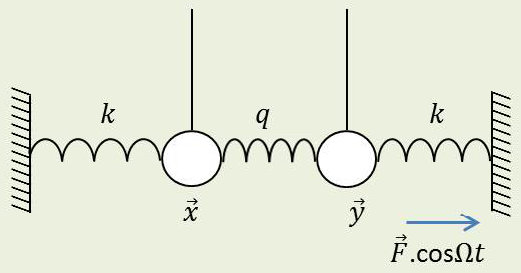Considérons par exemple les deux pendules ci-contre, couplés par élasticité.

On désigne par :

• \(x\) l’élongation du primaire soumis à la force extérieure \(F\exp(j~\Omega~t)\) ;

• \(y\) l’élongation du secondaire.

Les équations du mouvement sont : \[\left\{ \begin{aligned} &m~\frac{d^2x}{dt^2}+(k+q)~x-q~y=F\exp(j~\Omega~t) &&\text{primaire}\\ &m~\frac{d^2y}{dt^2}+(k+q)~y-q~x=0 &&\text{secondaire} \end{aligned} \right.\]

Soient \(\omega',~\omega''\) les pulsations principales du système libre : \[\omega'=\sqrt{\frac{k}{m}}\quad;\quad \omega''=\sqrt{\frac{k+2~q}{m}}\]

Pour \(\Omega=\omega'\) ou \(\Omega=\omega''\), on a la résonance. Le mouvement se poursuit indéfiniment sans qu’aucune force \(F\) soit nécessaire.

Par suite, si l’on attaque le système couplé avec une force \(F~\exp(j~\Omega~t)\) avec \(\Omega=\omega'\) ou \(\Omega=\omega''\), son amplitude tend vers l’infini.

Pour \(\Omega=\omega=\sqrt{\cfrac{k+q}{m}}\), pulsation du pendule non couplé, on observe le phénomène d’antirésonance.

En effet, cherchons les solutions du système [1] en supposant qu’un léger amortissement, très faible mais non nul, permette la disparition du régime transitoire. Pour le mouvement permanent (système avec deuxième membre), les solutions sont de la forme : \[x=X~\exp(j~\Omega~t)\quad;\quad y=Y~\exp(j~\Omega~t)\]

Elles doivent vérifier [1], donc : \[\left\{ \begin{aligned} &X(-m~\Omega^2+k+q)-qY=F\\ &Y(-m~\Omega^2+k+q)-qX=0 \end{aligned} \right.\]

Étudions l’amplitude X du primaire.

Pour l’antirésonance, nous avons : \[\Omega=\sqrt{\frac{k+q}{m}}\qquad\text{donc :}\quad X=0~;~Y=\frac{F}{q}\]

L’oscillateur primaire ne bouge pas. C’est le secondaire qui oscille. C’est en cela que consiste l’antirésonance.

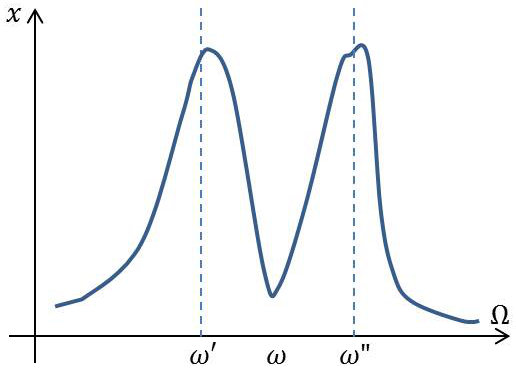En fait, les oscillateurs sont peu amortis. X et Y deviennent grands pour \(\Omega=\omega'\) ou \(\Omega=\omega''\) et X devient très petit pour \(\Omega=\omega\).

Quand \(\Omega\rightarrow 0\), le système se comporte comme un ressort. L’amplitude \(X\) tend vers une valeur finie et il en est de même pour \(Y\).

Quand \(\Omega\rightarrow\infty\), l’inertie devient prépondérante et l’amplitude \(X\rightarrow 0\) ainsi que \(Y\). On a donc pour la variation \(X(\Omega)\), deux maximums d’amplitude séparés par un minimum.

Expérience

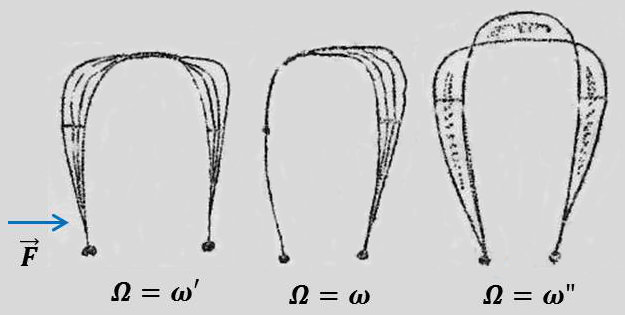Deux lames sont couplées par une corde à piano et excitées par un électroaimant. Nous observons (au moyen d’un stroboscope) les aspects successifs suivants :

1. Lames en phase

2. Antirésonnance

3. Lames en opposition de phase

5.1. Impédance d’un système couplé soumis à des oscillations forcées

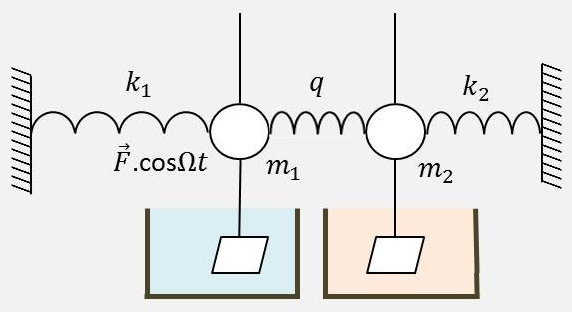Soient deux pendules amortis couplés et dont l’un est soumis à une force. Supposons les deux pendules différents avec des frottements visqueux différents.

Cherchons les équations d’un tel système.

Pour le (1) seul, (2) étant bloqué : \[m_1~\frac{d^2x}{dt^2}+R_1~\frac{dx}{dt}+(k_1+q)~x=0\]

Pour le (2) seul, (1) étant bloqué : \[m_2~\frac{d^2y}{dt^2}+R_2~\frac{dy}{dt}+(k_2+q)~y=0\]

Maintenant libérons les pendules et faisons agir la force sur le pendule (1).

On aura : \[[2]\qquad \left\{ \begin{aligned} &m_1~\frac{d^2x}{dt^2}+R_1~\frac{dx}{dt}+(k_1+q)~x-q~y=F~\exp(j~\Omega~t)\\ &m_2~\frac{d^2y}{dt^2}+R_2~\frac{dy}{dt}+(k_2+q)~y-q~x=0 \end{aligned} \right.\]

Ces deux équations définissent le mouvement du système couplé.

On aura un mouvement transitoire donné par la somme de la solution générale de l’équation sans second membre et de la solution particulière de l’équation avec second membre.

Le mouvement permanent sera donné par la solution particulière de l’équation avec second membre. Ce mouvement permanent est représenté par la solution particulière de la forme : \[[3]\qquad \left\{ \begin{aligned} &x=X~\exp(j~\Omega~t)\\ &y=Y~\exp(j~\Omega~t) \end{aligned} \right. \qquad\text{Les phases sont contenues dans X et Y.}\]

Nous devons savoir si [3] est solution de [2] : \[[4]\quad \left\{ \begin{aligned} &X~(-m_1~\Omega^2+j~R_1~\Omega+k_1+q)=F+q~Y\\ &Y~(-m_2~\Omega^2+j~R_2~\Omega+k_2+q)=q~X \end{aligned} \right.\]

Ces équations montrent que le primaire oscille de la même façon que si le secondaire était bloqué (pendule non couplé) et si on lui appliquait la force (\(F+q~Y\)). Le secondaire oscille comme s’il était non couplé et soumis à la force \(q~X\).

5.2. Calcul de l’impédance d’entrée du système couplé

Soient \(Z_1,~Z_2\) les impédances des deux pendules non couplés.

Posons : \[\frac{dx}{dt}=V_x~\exp(j~\Omega~t)\quad;\quad\frac{dy}{dt}=V_y~\exp(j~\Omega~t)\]

Par définition : \[V_x=\frac{F+q~Y}{Z_1}\quad;\quad V_y=\frac{q~X}{Z_2}\]

Le régime étant sinusoïdal : \[V_x=j~\Omega~X\quad;\quad V_y=j~\Omega~y\]

ce qui donne : \[Y=\frac{V_y}{j~\Omega}\quad\text{donc :}~~Y=\frac{q~X}{j~\Omega~Z_2}\quad\text{car :}~~V_y=\frac{q~X}{Z_2}\]

Ou encore : \[Y=\frac{q}{j~\Omega~Z_2}\Big(\frac{V_x}{j~\Omega}\Big)=\frac{-q~V_x}{\Omega^2~Z^2}\]

On a donc : \[V_x=\frac{F+q~Y}{Z_1}=\frac{F-\cfrac{q~V_x}{\Omega^2~Z_1}}{Z_1}\]

Ou encore : \[V_x~\Big(Z_1+\frac{q^2}{\Omega^2~Z_2}\Big)=F\]

Posant : \[V_x=\frac{F}{Z'}\]

Il vient : \[Z'=Z_1+\frac{q^2}{Z_2}\]

• \(Z_1\) : impédance du primaire non couplé

• \(Z_2\) : impédance du secondaire non couplé

• \(Z'\) : impédance d’entrée du système couplé

On dit que la force de rappel est fermée sur l’impédance d’entrée.

Rappelons que l’on appelle admittance la quantité \(A=\cfrac{1}{Z}\) .