1. Distance radiale

Une molécule est un assemblage de particules en interactions mutuelles :

• particules légères (électrons) ;

• particules lourdes (noyaux).

Selon l’approximation de Born et Oppenheimer, on peut admettre une grande différence d’inertie entre les électrons et les noyaux : \[\frac{m_e}{M_n}~\ll~1\qquad(1)\]

Selon Rutherford le modèle de la molécule est la sphère dont le rayon \(r_a\) englobe le noyau et atteint le nuage électronique : \[r_a~\approx~10^{-10}~\rm m~=~0,1~nm~=~100~pm\]

La toute première unité de mesure adaptée à l’atome a été nommée angstroem, de symbole Å, du nom d’un physicien suédois, l’un des inventeurs de la spectroscopie (1 Å = \(10^{-10}\) m).

Pour le rayon de l’atome d’hydrogène : \[a_0~\approx~0,5~\text{Å}\quad(\text{en fait}~0,528~\text{Å}~=~52,8~\rm pm)\]

Il faut noter que ce chiffre correspond à la probabilité de présence maximale (pour l’état fondamental) dans l’équation de Schrödinger de l’atome d’hydrogène, à cette distance.

L’interaction mutuelle de toutes les particules se traduit par la formule classique des forces coulombiennes avec un ordre de grandeur typique : \[f~\approx~\frac{q^2}{r^2}\]

Rappelons à ce propos la convention concernant la charge \(e\) de l’électron : \[q^2\qquad\rightarrow\qquad e^2=\frac{q2}{4\pi~\varepsilon_0}\]

Avec cette convention, l’expression littérale de \(a_0\) est :

\[a_0~=~\frac{\varepsilon_0~h^2}{\pi~m^*~e^2}~=~\frac{4\pi\varepsilon_0\hbar^2}{m^*~e^2}\qquad (m^*~:\text{masse réduite de l'électron})\qquad(2)\]

En fait, \(m^*\) peut être confondu avec \(m_e\), car, par définition : \[\frac{1}{m^*}~=~\frac{1}{m_e}~+~\frac{1}{M_n}\qquad\text{avec (1)}~:~\frac{m_e}{M_n}~\ll~1 \qquad(3)\]

Tous les atomes ont pratiquement le même ordre de grandeur (celui du vide lacunaire entre le noyau et le nuage électronique).

Dans la molécule, les mouvements des électrons sont finalement confinés dans un domaine de dimension de l’ordre de : \(2~a_0~\approx~1\rm\stackrel{o}{A}~=~0,1~nm\).

Les particules massives (noyaux) se déplacent beaucoup plus lentement que les particules légères (électrons) et elles gravitent autour de leurs centres d’attraction. Les électrons évoluent, plus ou moins, à la même distance du noyau.

Ce mouvement d’ensemble a fait dire au physicien Claude Cohen Tannoudji (prix Nobel 1997) d’une façon très imagée que les électrons habillent le noyau.

2. Énergie électronique

L’énergie élémentaire est celle de la masse de l’électron : \[E_{el}~\approx~\frac{1}{2}~\frac{\hbar^2}{2~(m~a_0^2)}\qquad(4)\]

2.1. Niveaux d’énergie

Dans l’atome d’hydrogène, les niveaux d’énergie sont donnés par : \[\left\{ \begin{aligned} &E_n~=~-\frac{E_I}{n^2}\\ &E_I~=~\frac{1}{2}~\frac{e^2}{4\pi~\varepsilon_0}~=~13,5~\rm eV\qquad(5) \end{aligned} \right.\]

2.2. Énergies de transitions

Les énergies de transitions entre niveaux (\(E_n-E_{n'}\)) sont de l’ordre de quelques électrons-volt.

Pour des ions hydrogénoïdes de charge \(Ze\) : \[E_n~=~-\frac{13,6}{n^2}~Z^2\qquad(\text{en~eV})\qquad(6)\]

3. Courbe d’énergie moléculaire

Considérons une molécule diatomique stable \(A-B\).

Soit \(D\) la distance inter-nucléaire. Il doit exister nécessairement une fonction \(E(D)\) associant une variation d’énergie à une variation de la longueur de la liaison \(A-B\).

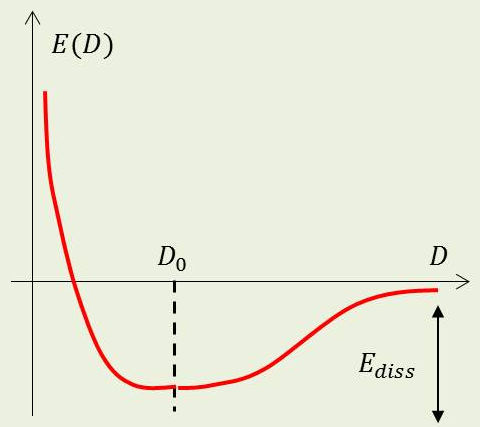D’où une allure de courbe :

• répulsive évidemment à courte distance ;

• présentant un minimum en une certaine valeur \(D_0\) ;

• tendant vers une constante quand \(D~\rightarrow~\infty\).

Il apparaît une énergie \(E_{diss}\) dite de dissociation.

Fait expérimental : une énergie de l’ordre du eV : \[E_{diss}~\approx~E_{el}\]

4. Mouvements nucléaires

Deux types de mouvements : vibration et rotation.

4.1. Vibration

Compte tenu des dimensions atomiques, la forme de la courbe au creux de potentiel peut être confondue avec sa parabole osculatrice (on retrouve en fait dans ce voisinage la courbe de l’oscillateur harmonique) :

\[\begin{aligned} E(x)~&\simeq~E(x_0)+\frac{1}{2}~k~(x-x_0)^2\\ k~&=~\Big(\frac{d^2E}{dx^2}\Big)_{x=x_0}\qquad;\qquad\frac{|\Delta x|}{x_0}~\ll~1\qquad\qquad(7)\end{aligned}\]

Imposons un étirement de l’ordre de \(x=2~x_0\).

Bien que cet étirement corresponde à deux fois la longueur de la liaison, l’augmentation d’énergie reste du même ordre de grandeur que l’énergie de dissociation.

Cette hypothèse permet d’écrire : \[~[~E(2x_0)-E(x_0)~]~\approx~E_{diss}\quad\Longleftrightarrow\quad\frac{1}{2}~k~x_0^2~\approx~\frac{\hbar^2}{4~m~a_0^2}\qquad(8)\]

La constante de raideur \(k\) a pour valeur approchée : \[k~\approx~\frac{\hbar^2}{4~m~a_0^4}\qquad\text{avec :}\quad x_0~\approx~2~a_0\qquad(9)\]

Ceci à un facteur 2 près sans influence, la dimension restant atomique.

Cette constante est de la forme : \[k=M~\omega_{vib}^2\qquad (M~:~\text{masse réduite des noyaux})\qquad(10)\]

Tous calculs faits, on obtient : \[E_{vib}~=~\hbar\omega_{vib}~\approx~\frac{\hbar}{(2~a_0)^2~\sqrt{m~M}}\qquad(11)\]

4.2. Rotation

Désignons respectivement par \(I\) et \(J\) le moment d’inertie et le moment cinétique.

L’énergie de rotation est du type (cf. mécanique classique) : \[E_{rot}~=~\frac{J^2}{2~I}\qquad;\qquad I~=~M~(2~a_0)^2\]

\(\qquad J~\approx~\hbar\) : ordre de grandeur fondamental

Par suite : \[E_{rot}~\approx~\frac{\hbar^2}{M~(2~a_0)^2}\qquad(12)\]

On peut établir, pour conclure, cette relation d’ordre entre les énergies : \[E_{rot}~\ll~E_{vib}~\ll~E_{el}\qquad(13)\]

5. Appendice

Nous ferons quelques remarques intéressantes en matière de calculs.

5.1. Constante \(\alpha\) des interactions électromagnétiques

Le terme (\(e^2/~\hbar\)) est homogène à une vitesse, comparable à \(c\), vitesse de la lumière.

\(\alpha\), constante fondamentale des interactions électromagnétiques, appelée parfois (abusivement) constante de structure fine est définie par : \[\alpha~=~\frac{e^2}{\hbar~c}~=~\frac{q^2}{4\pi~\varepsilon_0}~\frac{1}{\hbar~c}~\approx~\frac{1}{137}\qquad(\text{mesure expérimentale}~:~\frac{1}{\alpha}~=~137,035~977~9)\]

La valeur de \(\alpha\) étant petite et les effets de relativité étant exprimés par le facteur : \[\frac{v^2}{c^2}\approx~10^{-4}\]

on voit que l’on peut négliger ici les effets relativistes.

5.2. Rayon de Bohr

L’unité de longueur est le rayon de Bohr (grandeur typique de l’atome) : \[a_1~=~\frac{\hbar^2}{m_e~c^2}~=~\frac{1}{\alpha}~\frac{\hbar}{m_e~c}~\approx~0,53\rm \stackrel{o}{A}~=~53~pm\]

\(\qquad\cfrac{\hbar}{m_e~c}\) : longueur d’onde Compton de l’électron

5.3. Énergie de liaison

L’unité d’énergie de liaison a pour expression (et pour valeur) : \[E_l~=~\frac{m_ee^4}{2~\hbar^2}~=~\frac{1}{2}~m_e~c^2~\alpha^2~\approx~13,6~\rm eV\]

5.4. Échelle des temps atomiques

L’échelle des temps atomiques : \[\frac{2\pi~\hbar^3 }{m_e~e^4}~\approx~1,5\times 10^{-16}~\rm s~=~0,15~fs~(femtoseconde)\]

est la période de rotation de l’électron autour du proton pour l’énergie (\(-E_l\)).