1. Problème

Nous avons jusqu’à présent considéré un état stationnaire défini par {\(n,~l,~m\)} en négligeant le spin et ses effets relativistes. Pour rappel (tableau de correspondance) : \[\begin{matrix} &n=&1&2&3&4&5&6\\ &l=&0&1&2&3&4&5\\ & &s&p&d&f&g&h \end{matrix} \qquad\qquad 0~\leq~l~\leq~n-1\] \[\text{Exemples d'états} \qquad \left\{ \begin{aligned} &~~E_1~:~\{1s\}\qquad(\text{fondamental})\\ &~~E_2~:~\{2s,~2p\}\\ &~~E_3~:~\{3s,~3p,~3d\} \end{aligned} \right.\]

Cette représentation reste élémentaire. Des corrections nécessaires conduiront aux structures dites \(fines\) et hyperfines.

2. Structure fine

Dans l’hamiltonien d’un atome, les termes relativistes se divisent en deux catégories :

• les termes linéaires (par rapport aux opérateurs spins des électrons) ;

• les termes quadratiques :

  1. interaction (spin – orbite) : mouvement orbital des électrons avec leurs spins,

  2. interaction (spin – spin) entre les spins des électrons.

Les deux interactions sont du second ordre en comparaison avec la grandeur (\(v/c\)).

Cependant, dans les atomes lourds,

• l’interaction (spin – orbite) est très supérieure à l’interaction {spin-spin} ;

• l’interaction (spin – orbite) croît rapidement avec le numéro atomique \(Z\) ;

• l’interaction (spin – spin) ne dépend pas (pour l’essentiel) de \(Z\).

L’opérateur (spin – orbite) est représenté sous la forme (assimilable à une perturbation) : \[\widehat{V}_{sl}~=~\sum_a~\widehat{\textbf{A}}_a~\widehat{s}_a\qquad(\text{sommation sur tous les électrons})\qquad(1)\]

• \(\widehat{s}_a\) : opérateurs des spins des électrons

• \(\widehat{A}_a\) : opérateurs orbitaux agissant sur les fonctions des coordonnées

La principale contribution provient alors de la région des petites distances du noyau, de l’ordre de grandeur du rayon de Bohr \(r \) pour un noyau de charge \(Z~e\) : \[U(r)~\approx~\frac{Z~e^2}{r}~\approx~\frac{Z^2me^4}{\hbar^2}\qquad(\text{énergie potentielle})\]

De sorte que (\(\alpha\) déjà rencontrée comme constante de structure fine) \[\alpha~\approx~\frac{\hbar^2~U}{m^2~c^2~r^2}~\approx~Z^4~\Big(\frac{e^2}{\hbar c}\Big)^2~\frac{m~e^4}{\hbar^2}\qquad(2)\]

Le premier facteur croît rapidement avec \(Z\). Le deuxième facteur correspond à l’énergie fondamentale de l’électron périphérique.

Dans la moyenne sur les états électroniques de valeurs absolues \(L\) et \(S\) données du moment orbital et du spin totaux (directions non données), l’opérateur \(\widehat{V}_{sl}\) devient \(\widehat{V}_{SL}\).

Par raison de symétrie, les valeurs moyennes des \(\rm\widehat{s}_a\) doivent être dirigées suivant \(\rm\widehat{S}\), seul vecteur de spin à caractériser l’atome globalement.

De même, les moyennes des \(\rm\widehat{I}_a\) (moment orbital des électrons) sont dirigées suivant \(\rm\widehat{L}\).

De la sorte, on peut écrire : \[\widehat{V}_{SL}~=~A~\rm\widehat{S}~\widehat{L}\qquad(3)\]

\(A\) est une constante caractéristique du terme non désintégré, dépendant donc de \(S\) et \(L\) et non du moment total \(\textbf{J}\) de l’atome.

Pour calculer l’énergie de désintégration du niveau dégénéré (\(S\) et \(L\) données), il faut revenir à l’équation séculaire formée avec les éléments matriciels de l’opérateur.

Ici, les fonctions exactes de l’approximation zéro (matrice \(V_{SL}\) diagonale) sont connues : ce sont les fonctions d’onde des états avec des valeurs déterminées du moment total \(J\).

Calculer la valeur moyenne revient à remplacer l’opérateur \(\rm\widehat{S}~\widehat{L}\) par sa valeur propre : \[{\rm L~S}~=~\frac{1}{2}~\{J~(J+1)-L~(L+1)-S~(S+1)\qquad(4)\]

Toutes les composantes du multiplet étant à \(L\) et \(S\) identiques, seule nous intéresse leur disposition relative ; on peut écrire l’énergie de désintégration sous la forme : \[\frac{1}{2}~A~J~(J+1)\qquad(5)\]

Les intervalles entre composantes voisines (nombres \(J\) et \(J-1\)) valent donc : \[\Delta E_{J,~J-1}~=~A~J\qquad(6)\]

Formule qui exprime la règle des intervalles de Landé.

1) Lorsque \(A>0\), la composante la plus basse du niveau multiplet est le niveau de la plus petite valeur possible de J : \[J~=~|L-S|\]

De tels multiplets sont dits normaux.

2) Mais si \(A<0\), le niveau le plus bas est alors tel que : \[J~=~L+S\]

Le multiplet est dit inversé.

Règle pratique

Comment déterminer la valeur de \(J\) dans l’état normal de l’atome avec une couche incomplète ?

S’il s’y trouve au plus la moitié du nombre maximum possible d’électrons pour cette couche : \[J~=~|L-S|\]

Mais si la couche est plus que mi-pleine : \[J~=~L+S\]

3. Structure hyperfine

Autre effet atomique dû aux propriétés spécifiques du noyau : la désintégration des niveaux atomiques de l’énergie par suite de l’interaction des électrons avec le spin du noyau. C’est la structure hyperfine des niveaux.

Cette interaction étant faible, les intervalles de ladite structure sont très petits, même en comparaison des intervalles de la structure fine. Aussi la structure hyperfine doit-elle être examinée séparément, pour chacune des composantes de la structure fine.

Selon l’usage en spectroscopie atomique, nous désignerons le spin du noyau par \(i\), conservant la notation \(J\) du moment total de la couche électronique de l’atome.

Nous désignerons le moment total de l’atome, noyau compris, par \(F\)

Chaque composante de la structure hyperfine est caractérisée par une valeur déterminée de ce moment. En vertu des règles générales de l’addition des moments : \[F~=~J+i,~J+i-1,~\dots,~|J-i|\qquad(7)\]

De sorte qu’en tout, chaque niveau correspondant à \(J\) donné se scinde en :

\[\begin{aligned} 2~i+1 &\qquad\text{si~:}\quad~i~<~J\\ 2~J+1 &\qquad\text{si~:}\quad~i~>~J\end{aligned}\]

Les distances moyennes \(r\) des électrons dans l’atome étant grandes en comparaison du rayon \(R\) du noyau, le principal rôle dans la désintégration hyperfine incombe à l’interaction avec les moments multipolaires du noyau les plus bas. C’est le cas des moments magnétique dipolaire et électrique quadrupolaire.

Le moment magnétique du noyau a pour ordre de grandeur : \[\mu_{noy}~\approx~\frac{e~R~v_{noy}}{c}\]

• \(v_{noy}\) : vitesses des nucléons dans le noyau

Énergie d’interaction du moment magnétique du noyau avec celui de l’électron : \[E_{int}~=~\frac{\mu_{noy}~\mu_{el}}{r^3}~\approx~\frac{e^2~\hbar}{m~c^2}~\frac{R~v_{noy}}{r^3}\qquad(8)\]

Moment quadrupolaire du noyau : \[Q~\approx~e~R^2\]

Énergie d’interaction qu’il crée avec la charge de l’électron : \[E_{int}~=~\frac{e~Q}{r^3}~\approx~\frac{e^2~R^2}{r^3}\qquad(9)\]

L’opérateur d’interaction magnétique des électrons avec le noyau a la forme : \[\widehat{\rm V}_{iJ}~=~a~\rm\widehat{i}~~\widehat{J}\qquad(10)\]

Dépendance par rapport à \(F\) de la désintégration des niveaux qu’elle provoque : \[\frac{a}{2}~F~(F+1)\qquad(11)\]

Tous calculs faits, l’expression de la désintégration quadrupolaire hyperfine en fonction du nombre quantique \(F\) est : \[\frac{b}{2}~F^2~(F+1)^2+\frac{b}{2}~F~(F+1)~\{1-2~J~(J+1)-2~i~(i+1)\}\qquad(12)\]

4. Structures fine et hyperfine : étude de cas

En se plaçant dans la base propre de : \[\{\widehat{L}^2~,~\widehat{S}^2~,~\widehat{J}^2~,~\widehat{I}^2~,~\widehat{F}^2\}\qquad(F=J+I)\]

On peut dire qu’un niveau d’énergie est en réalité caractérisé par :

• 5 nombres {\(n,~l,~s,~j,~m_j\)} si l’on s’arrête à la structure fine ;

• 7 nombres {\(n,~l,~s,~j,~i,~F,~m_F\)} en poursuivant à la structure hyperfine.

4.1. Niveau 1

Le niveau 1 est caractérisé par \(l=0\) et \(s=1/2\) (spin de l’électron) : \[|l-s|~\leq~j~\leq~l+s\qquad\Rightarrow\qquad j=\frac{1}{2}\]

En structure fine, le niveau se note \(s_{1/2}\) (indice = valeur de \(j\)).

On doit avoir de plus : \[|j-i|~\leq~F~\leq~j+i\qquad\text{avec}~~i=\frac{1}{2}~\text{(spin du proton)}\]

Ce qui conduit à \(F=0\) et \(F=1\).

Il existe donc, en structure superfine, deux niveaux notés : \[1s_{1/2}~F=0\qquad\text{et}\qquad~1s_{1/2}~F=1\]

4.2. Niveau 2

À la structure fine, on obtient : \[\left\{ \begin{aligned} &2s_{1/2}\\ &2p_{1/2}\\ &2p_{3/2} \end{aligned} \right.\]

À la structure hyperfine, on obtient : \[\left\{ \begin{aligned} &2s_{1/2}F=0\\ &2s_{1/2}F=1 \end{aligned} \right. \qquad \left\{ \begin{aligned} &2p_{1/2}F=0\\ &2p_{1/2}F=1 \end{aligned} \right. \qquad \left\{ \begin{aligned} &2p_{3/2}F=1\\ &2p_{3/2}F=2 \end{aligned} \right.\]

4.3. Représentation graphique

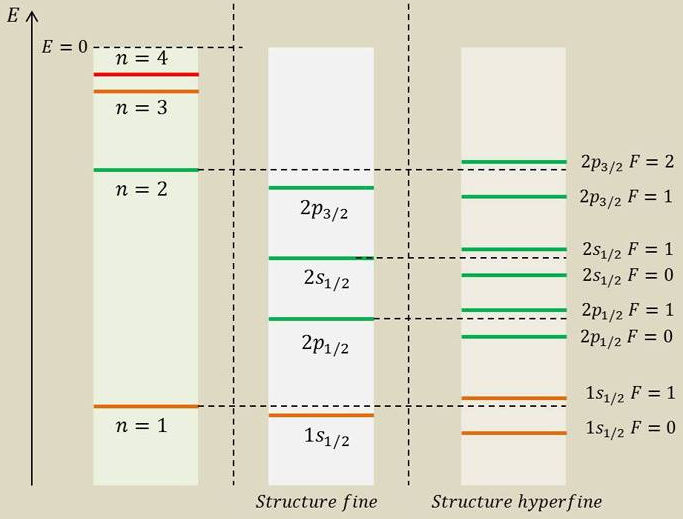Représentation des premiers niveaux de l’atome d’hydrogène, avec zooms sur la structure fine et la structure hyperfine des niveaux 1 et 2.

On remarquera qu’en structure fine, les niveaux \(2s_{1/2}\) et \(2p_{1/2}\) sont normalement dégénérés.