1. Fission et fusion : premières approches simplifiées

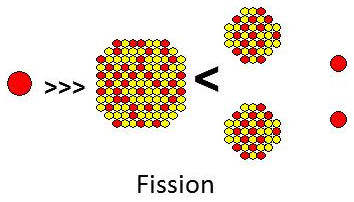La fission est la réaction nucléaire au cours de laquelle un noyau lourd se brise sous l’impact d’un neutron pour former deux noyaux plus légers.

Exemple de l’uranium 235 transformé en strontium 94 et xénon 140 : \[\rm _0^1n~+~_{92}^{235}U\quad\rightarrow\quad _{38}^{94}Sr~+~_{54}^{140}Xe~+~2~_0^1n~+~\text{énergie}\]

Le strontium et le xénon ont des énergies moyennes de liaison plus élevées que celle de l’uranium 235. Cette réaction libère une énergie de l’ordre de 186 MeV.

Les deux ou trois neutrons générés peuvent à leur tour amorcer d’autres réactions : phénomène d’avalanche ou réaction en chaîne (principe de la centrale nucléaire et de la bombe atomique).

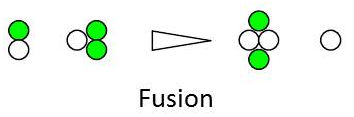La fusion est la réaction nucléaire au cours de laquelle deux noyaux légers vont s’unir pour donner un noyau plus lourd.

Nous avons pris ici l’exemple du deutérium et du tritium : \[\rm _1^2H~+~_1^3H\quad\rightarrow\quad _2^4He~+~_0^1n\]

Nous verrons plus tard que l’hélium 4 possède une énergie moyenne de liaison par nucléon plus élevée que celle des hydrogènes 1 et 2. La réaction libère en moyenne une énergie de l’ordre de 18 MeV.

La fusion nucléaire nécessite une pression et une température extrêmement élevées afin que les noyaux soient suffisamment confinés et énergétiques pour déclencher la réaction.

2. Neutron, agent de fission

2.1. Trajet du neutron

Avant de poursuivre l’étude de la fission et voir comment une réaction en chaîne peut s’entretenir, nous allons décrire les autres réactions que les neutrons sont susceptibles de provoquer.

Que peut faire un neutron se déplaçant dans un certain volume de matière ? Quelles réactions peut-il provoquer sur les noyaux la constituant ?

Plusieurs phénomènes s’excluant peuvent se produire :

1. Le neutron ne rencontre aucun noyau. Il sort du volume considéré sans avoir provoqué de réaction.

2. Le neutron rencontre un autre noyau et se réfléchit sur lui; il y a un choc type boule de billard qui se produit, sans perte d’énergie cinétique. Ce neutron peut ensuite soit quitter le système soit subir un des sorts décrits ci-après.

3. Le neutron pénètre dans le noyau et commence donc par former un isotrope du noyau initial. Il peut alors se présenter plusieurs cas :

   1. L’isotrope ainsi formé est stable.

   2. L’isotrope formé est radioactif. Il se désintègre en émettant suivant les cas des rayonnements \(\alpha\), \(\beta\) ou \(\gamma\) ou neutrons. L’ensemble de ces deux phénomènes s’appelle la capture.

   3. L’isotrope se disloque instantanément en un temps de l’ordre de \(10^{-14}\) s et cette dislocation peut s’effectuer suivant deux processus principaux :

      • Il y a réémission d’un neutron. Le noyau est donc revenu à son état initial, mais il y a une perte d’énergie cinétique. Cette perte est compensée par l’émission d’un rayonnement \(\gamma\) ; on parle alors de choc inélastique.

      • Il y a fission, c’est-à-dire que le noyau initial se coupe en deux morceaux principaux ayant des nombres de masse voisin et il émet en même temps quelques neutrons.

2.2. Environnement de la cible du neutron

Pour chiffrer les probabilités qu’un neutron a de provoquer telle ou telle réaction, il est commode d’introduire la notion de section efficace.

Considérons un cube de 1 cm de côté contenant \(N\) noyaux identiques qui ne peuvent provoquer qu’une seule réaction : la capture par exemple.

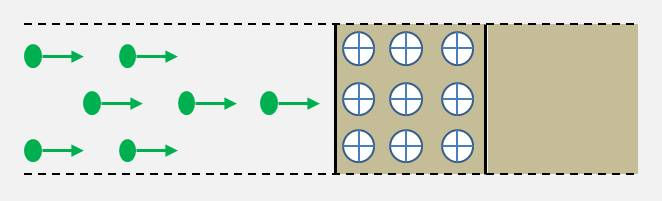Ce cube, considéré comme une cible, est bombardé par un faisceau de neutrons ayant tous la même vitesse \(v\), perpendiculaire à une face du cube. Provenant d’une source très éloignée, ce faisceau est supposé homogène et contient \(n\) neutrons par cm³.

Il est évident que les neutrons qui pénètreront dans le cube pendant une seconde sont ceux dont la distance au cube est inférieure à \(v\). Ils sont donc contenus dans un parallélépipède de hauteur \(v\) ayant une base de 1 cm².

Leur nombre est égal à \(n~v\), quantité généralement désignée par \(\varphi\) et appelée flux neutronique. Les valeurs courantes de ce flux sont de l’ordre de \(10^{13}-10^{14}~\rm n~cm^{-2}~s^{-1}\).

Finalement, on a un cube qui contient \(N\) noyaux et qui est traversé pendant une seconde par \(n~v\) projectiles ; on peut toujours écrire que le nombre de réactions qui se produisent en une seconde dans le cube de 1 cm³ est : \[n~v~N~\sigma~=~\varphi~N~\sigma\]

La quantité \(\sigma\) ainsi définie est appelée section efficace de capture.

Elle est de même nature qu’une surface et s’exprime dans une unité appelée barn, très petite, de \(10^{-24}\) cm².

Noter que l’on définit de manière analogue une section efficace pour chaque type : capture, fission, choc élastique.

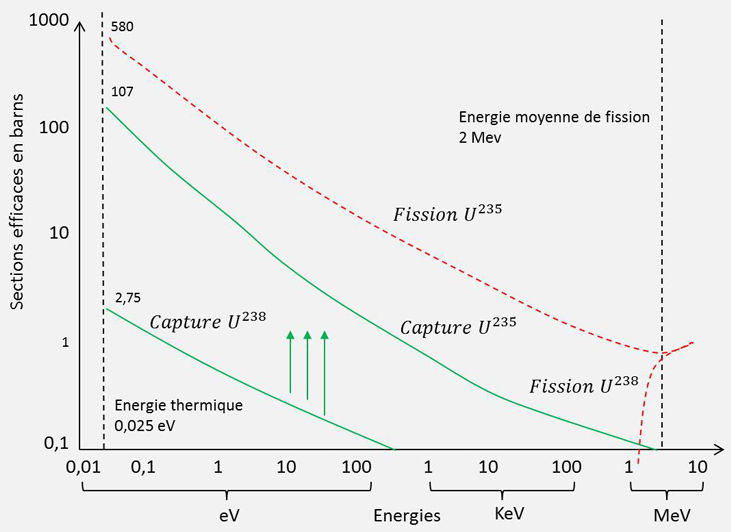
La figure ci-contre donne une idée des surfaces de capture pour l’uranium 235 et l’uranium 238.

On remarquera que :

• \(^{235}\rm U\) est fissile sans solution de continuité, depuis 10 MeV jusqu’à l’énergie thermique ;

• \(^{238}\rm U\) n’est fissile que pour les énergie supérieures à 1 MeV, et la section efficace est faible, inférieure à 1 barn.

Enfin la section de capture de \(\rm ^{235}U\) est beaucoup plus importante que celle de \(\rm ^{238}U\), abstraction faite des raies de résonance.

3. Fission. Types de réactions

Dans un processus de fission, le noyau d’un atome lourd (U ou Pu en particulier) est fragmenté en plusieurs nucléides plus légers. Il est accompagné d’une émission de neutrons et d’un dégagement important d’énergie.

On distingue deux types de fission : la fission dite spontanée et la fission dite induite.

– Dans une fission spontanée, le noyau se désintègre en plusieurs fragments sans qu’il y ait absorption de particule subatomique.

Ce type de fission n’est possible que pour des noyaux extrêmement lourds, tels que \(^{235}\rm U\) et \(^{240}\rm Pu\) ou \(^{244}\rm Pu\). Cela s’explique par le fait que l’énergie de liaison par nucléon est alors plus petite que pour les noyaux moyennement lourds nouvellement apparus.

– Il y a fission induite lorsqu’un noyau lourd capture une autre particule, généralement un neutron et que la noyau ainsi composé se désintègre en plusieurs fragments.

On peut prendre l’exemple de \(^{235}\rm U\) avec l’absorption d’un neutron : \[\rm _{92}^{235}U~+~_0^1n\quad\rightarrow\quad _{92}^{236}U\quad\rightarrow\quad X~+~Y~+~k~_0^1n\]

Les noyaux X et Y sont les produits de fission. Ils sont moyennement lourds et généralement radioactifs.

Exemple plus précis avec le krypton et le baryum : \[\rm _{92}^{235}U~+~_0^1n\quad\rightarrow\quad _{92}^{236}U\quad\rightarrow\quad _{36}^{92}Kr~+~_{56}^{141}Ba~+~3~_0^1n\]

Deuxième type de réaction avec le strontium et le xénon, accompagnée d’une énergie dissipée sous forme électromagnétique : \[\rm _{92}^{235}U~+~_0^1n\quad\rightarrow\quad _{92}^{236}U\quad\rightarrow\quad _{38}^{94}Sr~+~_{54}^{140}Xe~+~2~_0^1n~+~\gamma\]

La partie principale de l’énergie libérée se retrouvera dans l’énergie cinétique des deux atomes créés. Quant aux neutrons émis (généralement rapides), ils vont réagir avec les noyaux rencontrés : ils seront soit diffusés, soit renvoyés dans une direction différente, soit absorbés.

3.1. Bilan neutronique et répartition des masses

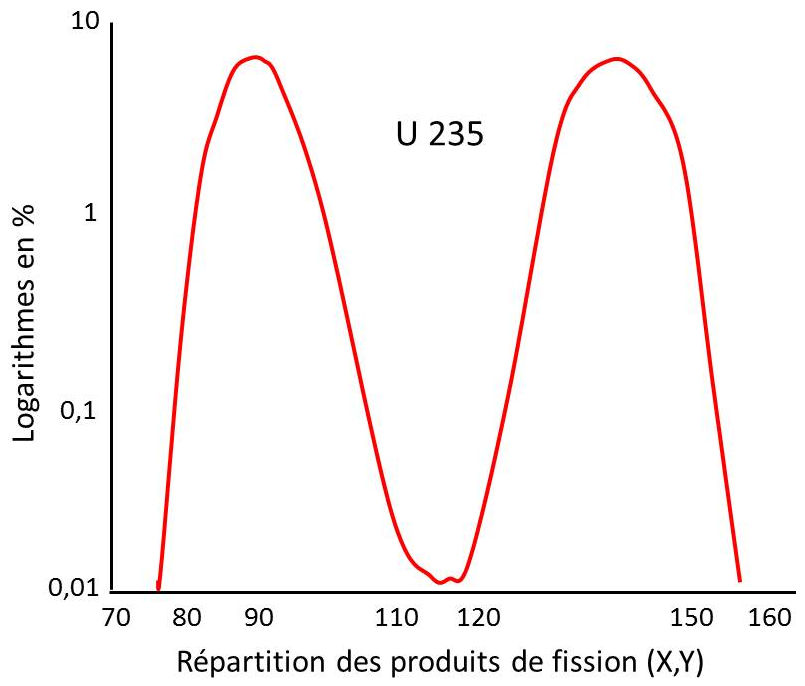Lors de la fission, des neutrons rapides sont tout de suite émis (10\(^{-14}\) s). Après émission de ces neutrons, les produits de fission commencent leur décroissance radioactive, ce qui va engendrer la libération de neutrons rapides avec une latence moyenne de 13 s.

Ces neutrons, libérés juste après des désintégrations \(\beta\), sont appelés retardés.

La distribution en masse des produits de fission suit une courbe dite en bosses de chameau. Ci-contre la courbe concernant l’uranium 235.

On peut remarquer que la fission crée des noyaux de nombres de masse autour de A = 95 (brome, strontium et zirconium) pour l’un des fragments et autour de A = 139 (iode, xénon et baryum) pour l’autre fragment.

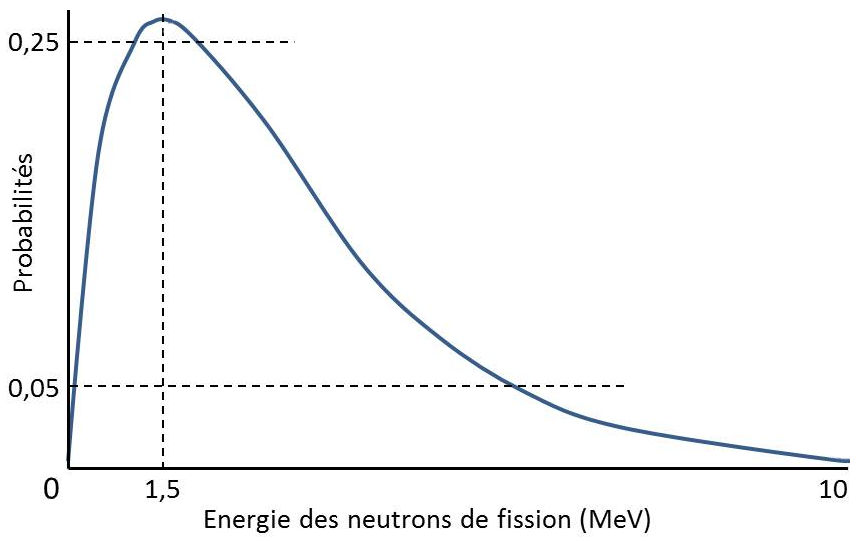L’énergie de fission a pu être étudié en fonction des probabilités énergétiques des protons responsables du processus.

La courbe ci-contre représente les probabilités en énergie (ou vitesse) des neutrons issus des produits de fission de l’uranium 235.

L’essentiel des neutrons ont une énergie comprise entre 0,25 et 4 Mev. Il n’y a guère de neutrons ayant une énergie supérieure à 6 MeV. On peut noter que pour 10 MeV la probabilité correspondante est à peine de 0,33 %.

On a pu établir que la vitesse moyenne des neutrons de fission est de l’ordre de 19 280 km/s.

3.2. Masse critique

La masse critique d’un matériau fissile est la quantité de ce matériau nécessaire au déclenchement d’une réaction nucléaire en chaîne de fission nucléaire. Elle dépend des propriétés nucléaires du matériau considéré (section efficace de fission et nombre de neutrons produits par la fission), mais aussi de ses propriétés physiques (en particulier sa densité) de sa forme, de sa pureté.

Tous les neutrons ne sont pas forcément absorbés par un noyau fissile, d’autres sont absorbés par des impuretés, d’autres enfin sortent du matériau sans avoir rencontré un noyau à casser. Ainsi, en jouant sur la taille, la densité, la pureté, la forme, une plus grande proportion des neutrons va être efficace.

Pour une certaine quantité de matériau, on est sûr que la réaction enchaîne va démarrer : c’est la masse critique.

En entourant le matériau fissile d’un réflecteur de neutrons, on favorise la fusion, ce qui diminue la quantité nécessaire au déclenchement de la réaction. En revanche, la présence d’un absorbeur de neutrons au sein de ce milieu fissile entraîne l’effet contraire.

NB : Dans un réacteur nucléaire, le matériau dépasse bien sûr la masse critique, mais il y a réaction en chaîne, car on contrôle finalement le nombre de neutrons pour qu’il soit stable. Ceci est obtenu par l’insertion ou le retrait de barres de contrôle contenant un absorbeur de neutrons (bore ou cadmium).

4. Fusion nucléaire

4.1. Principe

La fusion nucléaire est également appelée fusion thermonucléaire. Elle existe depuis l’origine des temps et de manière naturelle dans le Soleil et la plupart des étoiles. Il existe d’ailleurs une astrophysique nucléaire.

Dans ce processus, deux noyaux légers vont s’assembler pour former un noyau plus lourd. Cette fusion de noyaux légers dégage d’énormes quantités d’énergie provenant de l’attraction entre nucléons, due à une interaction forte (énergie de liaison).

La masse du nouvel atome obtenu par la fusion est inférieure à la somme des masses des deux atomes légers. Dans le processus, une partie de la masse est transformée en une énergie sous sa forme la plus simple : la chaleur.

Contrairement à la fission nucléaire, les produits de la fusion eux-mêmes (principalement de l’hélium 4) ne sont pas radioactifs, mais lorsque la réaction utilisée émet des neutrons rapides, ces derniers peuvent transformer les noyaux qui les capturent en isotopes pouvant l’être.

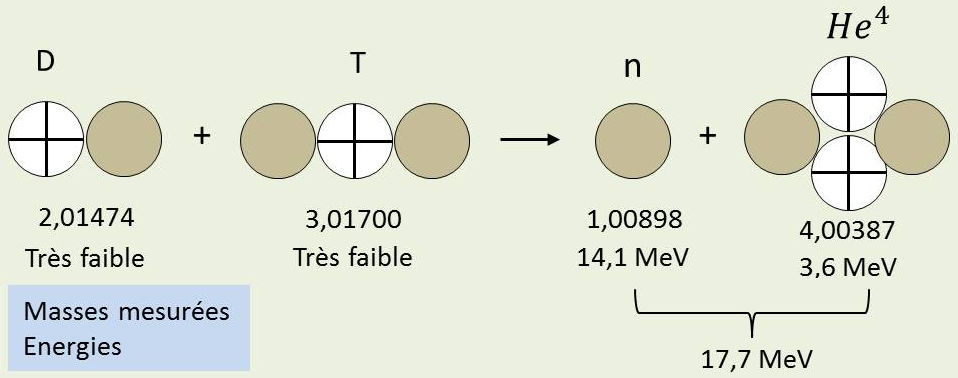Réactions classiques à partir de l’atome d’hydrogène :

\[\begin{aligned} \rm D+D~&\rightarrow~T+n+4~MeV \\ \rm D+D~&\rightarrow~n+H_e^3+3,28~MeV \\ \rm D+T~&\rightarrow~n+H_e^4+17,6~MeV\end{aligned}\]

• D : deuton (deutérium), noyau de l’hydrogène lourd (1 p + 1 n)

• T : triton (tritium), noyau de l’isotope supérieur (1 p + 2n)

On note une différence de masse de 0,01889, d’où l’on peut déduire l’énergie correspondante (formule d’Einstein : \(E~=~\Delta m~c^2\)).

4.2. Critère de Lawson

4.2.1. Expression de la formule

Le critère de Lawson permet d’exprimer la rentabilité de la réaction de fusion à partir de deux quantités :

• \(P_r\) : puissance générée par la réaction

• \(P_d\) : puissance dissipée (ou perdue)

Suivant les lois de la thermodynamique, la densité d’énergie stockée sous forme d’agitation thermique s’écrit : \[W~=~\frac{3}{2}~(n_e+\Sigma n_i)~K~T\]

• \(n_e\) : concentration d’électrons

• \(n_i\) : concentration d’ions de différentes espèces

• \(K\) : constante de Boltzmann

On peut écrire par ailleurs : \[P_d~=~\frac{W}{\tau_c}\qquad\qquad\tau_c~:~\text{temps de confinement}\]

La puissance générée peut s’exprimer par : \[P_r~=~\lambda~E_r\]

• \(E_r\) : énergie individuelle générée par la réaction

• \(\lambda\) : taux de réaction volumique

Nous considérons le cas d’une réaction à deux espèces de concentrations respectives \(n_1\) et \(n_2\) inter-réagissant : \[\lambda~=~n_1~n_2~<\sigma~v>\]

• \(<\sigma~v>\) : valeur moyenne du produit de la section efficace de la réaction à la vitesse relative des deux réactifs

On en déduit : \[n_e~\tau_c~>~\frac{3}{2}~\frac{n_e~(n_e+n_1+n_2)}{n_1~n_2}~\frac{K~T}{E_r<\sigma~v>}\]

4.2.2. Exemple du deutérium – tritium

Dans ce cas particulier : \[n_1~=~n_2~=~\frac{1}{2}~n_e\]

D’où la formule simplifiée : \[n_e~\tau_c~>~12~\frac{K~T}{E_r<\sigma~v>}~\equiv~L\]

\(K~T\) étant homogène à une énergie, il ne reste (du point de vue homogénéité) que le terme de surface \(\sigma\) et le terme de vitesse \(v\). La quantité \(L\) s’exprimera donc en \(\rm s~m^{-3}\).

Revenant à l’expression de l’inégalité.

Dans le membre de droite (noté \(L\) pour Lawson), toutes les quantités sont uniquement dépendantes de la physique fondamentales du processus de fusion considéré. En particulier, (\(T / <\sigma~v>\)) dépend uniquement de la température et l’on peut en trouver la valeur minimale. Le membre de droite dépend du dispositif mis en place pour réaliser la fusion.

Ainsi le critère de Lawson peut-il se réécrire comme une contrainte sur le produit de la concentration des réactifs par le temps de confinement qui doit être supérieur à une valeur fixée par la physique de la réaction.

Le fait qu’il soit nécessaire d’avoir le plus grand temps de confinement possible s’interprétera par le fait que les pertes d’énergie se font d’autant plus lentement que le temps de confinement est élevé (proportionnel à \(1/\tau_c\) ).

Quant à la nécessité d’avoir la plus grande concentration possible de réactifs, elle s’explique par le fait que le taux de réaction augmentera plus vite avec celle-ci que les pertes (respectivement en \(n_e^2\) et \(n_e\)).

5. Exercices d’application intéressants

5.1. Fission

Une réaction possible de la fission du noyau d’uranium 235 est : \[\rm _{92}^{235}U~+~_0^1n\quad\rightarrow\quad _{92}^{236}U\quad\rightarrow\quad _{38}^{94}Sr~+~_{54}^{140}Xe~+~2~_0^1n~+~\gamma\]

D’une part, il y a conservation du nombre de nucléons et de la charge électrique. D’autre part, il y a formation de plusieurs neutrons pour un neutron initiateur.

L’expression du bilan sera : \[E~=~(m_U~c^2+m_n~c^2)-(m_{Xe}~c^2+m_{Sr}~c^2+2~m_n~c^2)\]

Rappelons les valeurs des énergies moyennes de liaison : \[E'_U=7,590~{\rm MeV}\quad;\quad E'_{Sr}=8,583~{\rm MeV}\quad;\quad E'_{Xe}=8,290~\rm MeV\]

L’énergie de liaison est obtenue en multipliant cette énergie moyenne par les nombres de nucléons correspondants : \[E_U=1784~{\rm MeV}\quad;\quad E_{Sr}=808~{\rm MeV}\quad;\quad E_{Xe}=1161~{\rm MeV}\]

Tous calculs faits, \(E\) = 184,7 MeV. Cette énergie correspond à la perte d’énergie de masse lors de la réaction.

Ramenée à 1 g d’uranium, cette énergie serait : \[E'~=~\frac{E\times 6,02\times 10^{23}}{235}~=~4,73\times 10^{23}~\rm MeV~=~7,47\times 10^{10}~J\]

5.2. Fusion

Pour la réaction classique : \[\rm _1^2H~+~_1^3H\quad\rightarrow\quad _2^4He~+~_0^1n\]

l’énergie libérée est : \[E~=~(m_{^2H}~c^2+m_{^3H}~c^2]-[m_{^4He}~c^2+m_{^1n}~c^2)\]

Tous calculs faits : \[E~=~\{(3,0155+2,0136)-(4,0015+1,0087)\}~\times~931,5\quad\Rightarrow\quad 17,6~\rm MeV\]

Pour l’énergie libérée par 1 g de tritium : \[E'~=\frac{E\times 6,02 \times 10^{23}}{3}~=~3,53\times 10^{24}~\rm MeV\]

5.3. Bombardement neutronique

On désigne par :

• \(\Delta\nu\) : le nombre de réactions pendant un temps \(\Delta t\)

• \(S\) : la surface de la cible recouverte par le faisceau

• \(\Phi\) : le flux de neutrons

• \(x\) : l’épaisseur de la cible

• \(N_s\) : le nombre de noyaux de soufre 32 par unité de volume (cm\(^3\))

• \(\sigma\) : la surface d’un disque élémentaire affecté à chacun des atomes cibles

On veut établir la formule : \[\Delta\nu~=~S~\Phi~\Delta t~x~\sigma\]

Méthode :

Nombre d’atomes (cibles) dans la cible : \[N~=~S~x~N_s\]

Pour qu’une réaction se produise, le projectile doit rencontrer une surface : \[N~\sigma~=~S~x~N_s~\sigma \qquad(\text{surface totale de tous les petits disques }\sigma)\]

Le projectile arrive sur la surface \(S\). La probabilité pour qu’il provoque une réaction est : \[\text{Prob}~=~\frac{N~\sigma}{S}~=~x~N_s~\sigma\]

D’autre part, cette probabilité correspond au nombre \(\Delta\nu\) de réactions provoquées pendant \(\Delta t\) au nombre total de projectiles (neutrons) reçus par la cible pendant le même temps soit \(S~\Phi~\Delta t\) : \[\text{Prob}~=~\frac{\Delta\nu}{S~\Phi~\Delta t}~=~\frac{N~\sigma}{S}~=~N_s~\sigma\]

On a donc : \[\Delta\nu~=~N~\Phi~\sigma~\Delta t~=~S~\Phi~\Delta t~x~N_s~\sigma~=~N~\Phi~\sigma~\Delta t\]

D’où la variation de \(N\) sous forme d’équation différentielle : \[dN~=~-N~\Phi~\sigma~dt\]