1. Retour sur les équations de Maxwell
On doit tenir compte de la conductivité (\(\gamma\neq 0\)).
Premier groupe : \[\overrightarrow{i}=\gamma~\overrightarrow{E}\quad;\quad\overrightarrow{D}=\varepsilon~\overrightarrow{E}\quad;\quad\overrightarrow{B}=\mu~\overrightarrow{H}\]
Deuxième groupe : \[\left\{ \begin{aligned} &\overrightarrow{\rm rot}\overrightarrow{E}=-\frac{\partial\overrightarrow{B}}{\partial t}\\ &\overrightarrow{\rm rot}\overrightarrow{H}=\overrightarrow{i}+\frac{\partial\overrightarrow{D}}{\partial t}\\ &{\rm div}\overrightarrow{B}={\rm div}\overrightarrow{D}=0 \end{aligned} \right. \qquad\Rightarrow\qquad \left\{ \begin{aligned} &\overrightarrow{\rm rot}\overrightarrow{E}=-\mu~\frac{\partial\overrightarrow{H}}{\partial t}\\ &\overrightarrow{\rm rot}\overrightarrow{H}=\gamma~\overrightarrow{E}+\varepsilon~\frac{\partial\overrightarrow{E}}{\partial t}\\ &{\rm div}\overrightarrow{E}={\rm div}\overrightarrow{H}=0 \end{aligned} \right.\]
2. Propagation d’une onde sinusoïdale
On cherche une solution de la forme : \[E=E_0~e^{j~\omega~t}~e^{-j~\overrightarrow{k}\cdot\overrightarrow{r}}\quad;\quad |\overrightarrow{k}|=\frac{2~\pi}{\lambda}\]
Dans un milieu non conducteur (avec \(\overrightarrow{k}~//~Ox\)), nous avions : \[\overrightarrow{E}=\overrightarrow{E_0}~\exp\big\{j~\omega~\Big(t-\frac{x}{v}\Big)\big\}\quad;\quad v=\frac{1}{\sqrt{\varepsilon~\mu}}\]
et la relation de Maxwell : \[\overrightarrow{rot}\overrightarrow{H}=\varepsilon~\frac{\partial\overrightarrow{E}}{\partial t}\]
On écrira, dans le cas présent : \[\overrightarrow{rot}\overrightarrow{H}= \gamma~\overrightarrow{E}+\varepsilon~\frac{\partial\overrightarrow{E}}{\partial t}= (\gamma+j~\omega~\varepsilon)~\overrightarrow{E}= \Big(\varepsilon+\frac{\gamma}{j~\omega}\Big)~\frac{\partial\overrightarrow{E}}{\partial t}\]
On peut alors écrire : \[\overrightarrow{rot}\overrightarrow{H}=\varepsilon'~\frac{\partial\overrightarrow{E}}{\partial t}\qquad \text{avec, à priori :}\quad\varepsilon'=\varepsilon+\frac{\gamma}{j~\omega}\]
On prendra le même type de solution : \[v=\frac{1}{\sqrt{\mu~\varepsilon'}}=\frac{1}{\sqrt{\mu~(\varepsilon+\cfrac{\gamma}{j~\omega})}}\]
On obtient ainsi un indice complexe : \[n=\sqrt{\frac{\varepsilon'}{\varepsilon_0}}= \sqrt{\frac{\varepsilon}{\varepsilon_0+\cfrac{\gamma}{j~\omega~\varepsilon_0}}}=\nu-j~\chi\]
Ces deux paramètres sont obtenus par identification : \[\nu^2-\chi^2=\frac{\varepsilon}{\varepsilon_0}\qquad;\qquad \nu~\chi=\frac{\gamma}{2~\omega~\varepsilon_0}\]
En reprenant l’expression de la vitesse de propagation : \[v=\frac{c}{n}=\frac{c}{\nu-j~\chi}\qquad;\qquad \frac{1}{v}=\frac{\nu}{c}-j~\frac{\chi}{c}\]
D’où la nouvelle expression du champ électrique : \[E=E_0~\exp(j~\omega~t)~\exp\Big(-j~\omega~\nu~\frac{x}{c}\Big)~\exp\Big(-\omega~\chi~\frac{x}{c}\Big)\]
et pour l’amplitude : \[A=A_0~\exp\Big(-j~\omega~\nu~\frac{x}{c}\Big)~\exp\Big(-\omega~\chi~\frac{x}{c}\Big)\]
Dans ce qui précède, on a supposé que la propagation se faisait dans la direction des \(x>0\).
L’intensité a pour expression : \[I=A~A^*=E_0^2~\exp\Big(-\frac{2~\omega~\chi}{c}~x\Big)\]
On voit qu’elle décroît quand l’onde progresse dans le conducteur et l’absorption est d’autant plus rapide que \(\chi\) est grand. \(\chi\) est l’indice d’extinction. La constante \(\nu\) est l’indice de réfraction du métal.
On peut expliquer cette absorption de la manière suivante : dans le métal, le champ électrique produit un déplacement des électrons ; par suite, il y aura transformation de l’énergie lumineuse en énergie calorifique par effet Joule (densité \(\overrightarrow{i}^2/\gamma\)).
3. Réflexion normale sur une surface métallique
Dans le cas de la réflexion normale sur une surface métallique, les formules de Fresnel sont encore applicables, à condition de considérer que l’indice \(n_2\) est complexe : \[r=\frac{n_1-n_2}{n_1+n_2}\qquad\Rightarrow\qquad r=\frac{n_1-\nu+j~\chi}{n_1+\nu-j~\chi}\]
Pour le coefficient de réflexion en intensité : \[R=r~r^*=\frac{(n_1-\nu)^2+\chi^2}{(n_1+\nu)^2+\chi^2}\]
Comme \(r\) est complexe, il y aura une différence de phase entre la vibration incidente et la vibration réfléchie. Une transformation d’écriture donne facilement : \[r=\frac{(n_1^2-\nu^2-\chi^2)+2~j~n_1~\chi}{(n_1+\nu)^2+\chi^2}\quad\Rightarrow\quad \tan\varphi=\frac{2~n_1~\chi}{n_1^2-\nu^2-\chi^2}\]
Pour l’argent et pour la raie \(D\), on trouve : \[\nu=0,18\qquad\chi=3,67\qquad\tan\varphi=0,60\qquad\varphi=37~^o\]
Ce qui correspond à une différence de marche : \[\delta=\frac{\lambda~\varphi}{2~\pi}\approx\frac{\lambda}{10}\]
Remarques
D’une manière générale, \(\chi\gg\nu\) pour les métaux. En posant : \[r=\rho~e^{j~\varphi}=\rho~\cos\varphi+j~\rho~\sin\varphi\]
Il vient : \[\rho~\cos\varphi=\frac{n_1^2-\nu^2-\chi^2}{(n_1+\nu)^2+\chi^2}~~;~~\rho~\sin\varphi=\frac{2~n_1~\chi}{(n_1+\nu)^2+\chi^2}<0\quad\Rightarrow\quad\frac{\pi}{2}<\varphi<\pi\]
Si l’on fait \(\chi=0\), on retrouve l’avance de phase de \(\pi\) qui caractérise la réflexion de l’air sur un milieu transparent.
Dans les appareils de mesure comme le Fabry-Perrot, la séparatrice de Michelson, on doit tenir compte de ce déphasage avance.
4. Réflexion oblique sur une surface métallique
Le cas de la réflexion oblique sur une surface métallique est plus compliqué à étudier du fait de l’indice complexe qui ne permet pas d’appliquer la loi de Descartes au sens habituel du terme : \[n_1~\sin i_1=n_2~\sin i_2\qquad n_2\in\mathbb{C}\]
Mais il est évident que : \[n_1~\sin i_1\in\mathbb{R}\quad\Rightarrow\quad n_2~\sin i_2\in\mathbb{R}\]
Cependant, si l’on s’intéresse à \(\cos i_2\) et à la relation déduite de la loi de Descartes, on met en évidence le résultat suivant : \[n_2^2-n_1^2~\sin^2 i_1=n_2^2~\cos^2 i_2\]
qui montre que \(n_2~\cos i_2\) est une quantité complexe.
Les formules de Fresnel sont alors applicables, mais nous ne ferons pas le calcul qui est extrêmement compliqué et exige que certaines approximations soient réalisables.
5. Absorption et dispersion
Le vecteur induction électrique s’écrit : \[\overrightarrow{D}=\varepsilon~\overrightarrow{E}=\varepsilon_0~\overrightarrow{E}+\overrightarrow{P}\]
\(\overrightarrow{P}\) est la polarisation du milieu, c’est à dire le moment électrique par unité de volume qu’il acquiert sous l’action du champ \(\overrightarrow{E}\).
Si nous considérons une charge \(e\) écartée de \(x\) de sa position d’équilibre, sa contribution au moment électrique est \(\overrightarrow{p}=e~\overrightarrow{x}\). S’il y a \(N\) charges identiques ayant les mêmes \(\overrightarrow{x}\) , la polarisation sera : \[\overrightarrow{P}=N~\overrightarrow{p}+N~e~\overrightarrow{x}\]
5.1. Calcul de l’indice complexe
À l’action directe du champ \(\overrightarrow{E}\), il faut ajouter une action indirecte par l’intermédiaire de la polarisation \(\overrightarrow{P}\) du milieu, due à \(\overrightarrow{E}\), et qui agit aussi sur \(e\). On remplacera alors \(\overrightarrow{E}\) par \(\overrightarrow{E'}=\overrightarrow{E}+a~\overrightarrow{P}\), \(a\) étant une constante que l’on peut calculer.
Étudions donc le mouvement d’une charge e : \[m~\ddot{x}+f~\dot{x}+k~x=e~(E+a~P)\]
Ou encore : \[m~\ddot{x}+f~\dot{x}+(k-N~e^2~a)~x=e~E\]
Adoptons les notations : \[\omega_0^2=\frac{k}{m}\qquad;\qquad\beta=\frac{f}{m}\]
Le champ électrique est de la forme \(E=E_1~e^{j~\omega~t}\), ce qui conduit à rechercher pour \(x\) une solution de la forme \(x=X~e^{j~\omega~t}\). L’équation différentielle devient : \[\Big\{-\omega^2+j~\omega~\beta+\omega_0^2-\frac{N~e^2~a}{m}\Big\}~X=\frac{e}{m}~E_1\]
On a donc : \[X=\frac{e}{m}~E_1~\frac{1}{-\omega^2+j~\omega~\beta+\omega_0^2-\cfrac{N~e^2~a}{m}}\]
Par ailleurs : \[P=N~e~X\quad\Rightarrow\quad P=\frac{N~e^2}{m}~E_1~\frac{1}{-\omega^2+j~\omega~\beta+\omega_0^2-\cfrac{N~e^2~a}{m}}\]
On peut maintenant revenir à l’indice, sachant que \(n^2=\varepsilon/\varepsilon_0\) : \[\varepsilon~E=\varepsilon_0~E+P=\varepsilon_0~E~\Big(1+\frac{P}{\varepsilon_0~E}\Big)\]
Par suite : \[n^2=1+\frac{P}{\varepsilon_0~E}\quad\Rightarrow\quad n^2-1=\frac{P}{\varepsilon_0~E}\]
Et finalement : \[n^2-1=\frac{N~e^2}{\varepsilon_0~m}~\frac{1}{-\omega^2+j~\omega~\beta+\omega_0^2-\cfrac{N~e^2~a}{m}}\]
On a intérêt à faire apparaître une fonction de \(n\) qui soit proportionnelle à \(N\) : \[\frac{n^2-1}{n^2-1+\cfrac{1}{a}}=a~\frac{N~e^2}{\varepsilon_0~m}~\frac{1}{-\omega^2+j~\omega~\beta+\omega_0^2}\]
Les calculs effectués par H.A. Lorentz et L. Lorentz ont conduit à la valeur \(a = 1/3\), d’où la formule dite de Lorentz-Lorentz : \[\frac{n^2-1}{n^2+2}=~\frac{Ne^2}{3~\varepsilon_0~m}~\frac{1}{-\omega^2+j~\omega~\beta+\omega_0^2}\]
Si on généralise à plusieurs types de charges mobiles, on obtient la formule de Ketteler-Helmoltz : \[\frac{n^2-1}{n^2+2}=~\sum_i \frac{N_i}{3~\varepsilon_0}~\Big(\frac{e^2}{m}\Big)_i~\frac{1}{-\omega^2+j~\omega~\beta+\omega_0^2}\]
Enfin, si la pulsation \(\omega\) est suffisamment éloignée de la fréquence propre, on peut négliger \(\omega\) devant le terme \((\omega_{0i}^2-\omega^2)\) et on obtient ainsi la formule de Sellmeier : \[n^2-1=\sum_i \frac{N_i~e_i^2}{\varepsilon_0~m_i}~\frac{1}{{\omega'}_{0i}^2-\omega^2}\quad;\quad {\omega'}_{0i}^2=\omega_{0i}^2-\frac{a~N~e^2}{m}\]
L’indice est alors réel et l’on se trouve dans une région de transparence.
5.2. Courbes de dispersion
Le signe \(\sum\) montre que l’on doit sommer les effets de toutes les fréquences propres \(\omega_0\) correspondant à des bandes d’absorption.
Pour fixer les idées et pour commencer, examinons le cas d’une seule bande d’absorption : \[n^2-1=\sum_i \frac{N~e_i^2}{\varepsilon_0~m}~\frac{1}{{\omega'}_{0i}^2-\omega^2}\]
On sait que \(\omega=\cfrac{2~\pi~c}{\lambda}\). On a donc : \[n^2=1+\frac{N~e^2}{\varepsilon_0~m}~\frac{\lambda_0^2}{4~\pi^2~c^2}~\Big\{\frac{\lambda^2}{\lambda^2-\lambda_0^2}\Big\}\]
Donc de la forme : \[n^2=1+\frac{D}{1-\cfrac{\lambda_0^2}{\lambda^2}}=1+D~\Big\{1+\frac{\lambda_0^2}{\lambda^2}+\frac{\lambda_0^4}{\lambda^4}+\dots\Big\}\]
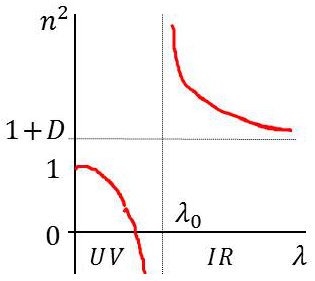 Forme dite de Cauchy : \[n^2=A+\frac{B}{\lambda^2}+\frac{C}{\lambda^4}\]
Forme dite de Cauchy : \[n^2=A+\frac{B}{\lambda^2}+\frac{C}{\lambda^4}\]
La courbe représentative de \(n^2(\lambda)\) montre que, dans le domaine de \(\lambda_0\), l’ultraviolet (\(\lambda\) très petit), l’indice de réfraction est inférieur à l’unité.
Les portions caractérisées par les lignes grises, donc au voisinage de \(\lambda_0\), correspondent à des zones dans lesquelles l’approximation \(\beta~\omega=0\) n’est plus valable, car \(\beta~\omega~\approx\omega_0\).
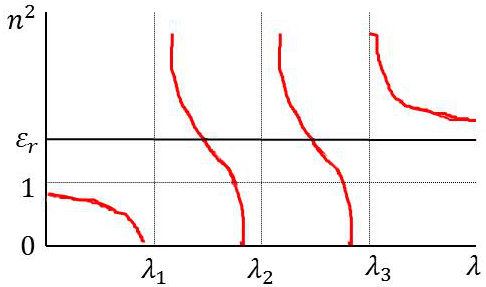 L’étude est facilement transposable au cas de trois bandes d’absorption \(i=1,~2,~3\).
L’étude est facilement transposable au cas de trois bandes d’absorption \(i=1,~2,~3\).
Dans un calcul plus poussé, on s’apercevrait que la valeur \((1+D)\) correspond au coefficient \(\varepsilon\) statique (pour \(\lambda=\infty\), c’est à dire pour \(\omega=0\)).
5.3. Relation indice - intensité
Reprenons la formule de Lorentz-Lorentz avec \(\beta~\omega=0\) : \[\frac{n^2-1}{n^2+2}=\frac{N~e^2}{3~\varepsilon_0~m}~\frac{1}{\omega_0^2-\omega^2}\qquad;\qquad N=\frac{N_{Av}~d}{M}\]
\(N_{Av}\) : nombre d’Avogadro\(M\) : masse moléculaire\(d\) : densité
On appelle réfractivité moléculaire l’expression : \[[n]=\frac{n^2-1}{n^2+2}~\frac{M}{d}=N_{Av}~\frac{e^2}{3~\varepsilon_0~m}~\frac{1}{\omega_0^2-\omega^2}\]
\([n]\) est invariant pour une espèce moléculaire donnée, quel que soit son état.

