1. Introduction

Pour la mécanique le temps et l’espace sont absolus. Il existe une sensation du temps. On sait distinguer la cause de l’effet. Un rapide horizon des mesures du temps : les clepsydes (récipients dont l’eau se vidait lentement), les pendules (au XVII° siècle), les horloges et montres mécaniques, les horloges à quartz (précision de l’ordre de \(10^{-6}\) s), les masers, etc.

Pour la mécanique classique (newtonienne), le temps est absolu dans l’univers. Il s’écoule partout de la même manière. L’accord entre deux horloges \(H_1\) et \(H_2\) séparées par une distance \(L\) peut se faire par ondes radio ou par signaux optiques si l’on admet que la vitesse de la lumière est constante.

Un espace absolu suppose des corps immobiles, ce qui n’est pas le cas. Tous les corps sont mobiles les uns par rapport aux autres. C’est pourquoi les physiciens du XVII° siècle avaient créé un espace absolu mystérieux qu’ils appelaient éther. L’expérience de Michelson prévue pour vérifier l’existence de cet espace a échoué, mais il a heureusement conduit à introduire la relativité.

2. Référentiels

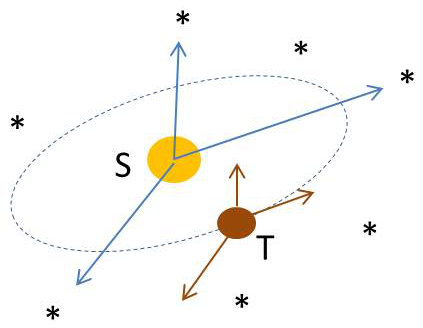Dans le référentiel de Copernic, le soleil est placé à l’origine et les axes sont dirigés vers trois étoiles fixes \(E_1\), \(E_2\), \(E_3\).

Ces étoiles sont-elles vraiment fixes ? On les suppose très éloignées pour admettre qu’elles sont fixes.

Pour Galilée, tout référentiel est animé d’un mouvement rectiligne et uniforme par rapport à celui de Copernic, centré sur le soleil.

3. Transformation de Galilée

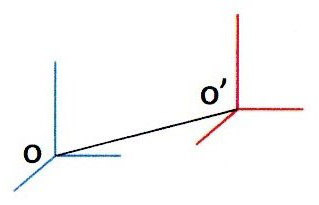Un événement \(E\) au point \(M(x,~y,~z)\) est caractérisé par les coordonnées \((x,~y,~z,~t)\).

Si on change de référentiel : \[M(x,~y,~z,~t)\rightarrow M'(x',~y',~z',~t')\]

On suppose qu’à l’instant \(t\), \(O'\) est en \(O\) et que \(OO' = v~t\).

Pour simplifier, on suppose que le déplacement se fait le long de l’axe des \(x\).

\[\left\{ \begin{aligned} x'&=x-v~t\\ y'&=y\\ z'&=z\\ t'&=t \end{aligned} \right. \qquad\text{et}\qquad \left\{ \begin{aligned} x&=x'-v~t'\\ y&=y'\\ z&=z'\\ t&=t' \end{aligned} \right.\] La transformation unité existe. La transformation de Galilée d’une transformation de Galilée est encore une transformation de Galilée. Il existe donc un groupe de Galilée ou groupe de la mécanique classique.

3.1. Les invariants

Passons d’un point \(M\) à un point très voisin \(M + dM\).

Si on effectue une dérivation par rapport à \(t\), on voit que \(dt' = dt\), \(dx' = dx\), \(dy' = dy\), \(dz'=dz\), de sorte que, pour les distances : \[(ds)^2 = (dx)^2+(dy)^2+(dz)^2 = (ds')^2=(dx')^2+(dy')^2+(dz')^2\]

On a donc \( dt'=dt\) et \(ds'=ds\) : les distances spatiale et temporelle sont des invariants dans la transformation.

4. Le principe fondamental

Qu’il s’agisse d’un repère de Copernic centré sur le système solaire ou d’un repère de Galilée en translation uniforme, on a toujours la relation entre force, masse et accélération : \(\vec{f}=m\vec{\gamma}\).
En postulant que la masse est invariante, cette formule est invariante dans la transformation de Galilée. En effet, en dérivant deux fois : \[\left\{ \begin{aligned} x'&=x-vt\\ y'&=y\\ z'&=z\\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \cfrac{dx'}{dt}&=\cfrac{dx}{dt}-v \\ \cfrac{dy'}{dt}&=\cfrac{dy}{dt} \\ \cfrac{dz'}{dt}&=\cfrac{dz}{dt} \\ \end{aligned} \right.\] \[\left\{ \begin{aligned} \cfrac{d^2x'}{dt^2}&=\cfrac{d^2x}{dt^2} \qquad \text{ou encore : }\quad\gamma'_x=\gamma_x \\ \cfrac{d^2y'}{dt^2}&=\cfrac{d^2y}{dt^2} \qquad \text{ou encore : }\quad\gamma'_y=\gamma_y \\ \cfrac{d^2z'}{dt^2}&=\cfrac{d^2z}{dt^2} \qquad \text{ou encore : }\quad\gamma'_z=\gamma_z \end{aligned} \right.\]

\(m\) et \(\gamma\) étant constants, \(\vec{f}\) est donc invariante.

Remarque

Considérons un ensemble de points 1, 2, ..., j. Le point 1 par exemple subira l’action de la gravitation de tous les autres. Ce que l’on exprimera par la relation classique liant la force dérivant d’un potentiel (au sens large du terme) exercé à une distance \(r\) : \[\overrightarrow{f}_1=\overrightarrow{\rm grad}\;\Phi(r_{1j})\] Comme les \(r_{1j}\) sont invariants, il en est de même pour \(\Phi\) et par conséquent de \(\overrightarrow{f}_1\).