1. Introduction
La transformation de Galilée est en désaccord avec les principes de la relativité. La loi classique de composition des vitesses est en désaccord avec le principe de constance de la vitesse de la lumière. Nous savons à présent qu’il faut associer un temps différent à chaque système galiléen, l’image du croisement des deux vaisseaux ayant montré qu’en relativité il faut écrire \(t' \neq t\).
Il faut rechercher une autre transformation liant \([x',v',t']\) et \([x,v,t]\) qui respecterait les principes de la relativité. Ce sera la transformation de Lorentz, du nom de celui qui l’a découverte vers 1900, avant Einstein, mais sans en avoir saisi la signification profonde. Pour Lorentz, la nouvelle variable temporelle était une simple grandeur mathématique. C’est Einstein qui a montré le caractère naturel et physique du temps relativiste.
2. Approche physique
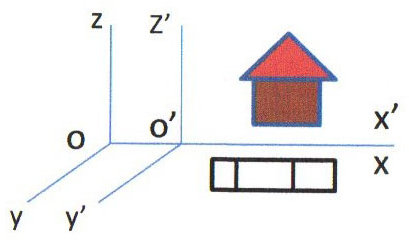Un événement \(E\) est repéré dans deux référentiels galiléens \(G\) et \(G'\). On écrit symboliquement : \[G:(x,~y,~z,~t)~~;~~G':(x',~y',~z',~t')~~;~~t'\neq t\]
Observons la représentation ci-contre. La maison est attachée au repère \(G\) et la voiture au repère \(G'\). Une étincelle est émise à la coïncidence des points \(O\) et \(O'\).
La lumière parvient à la maison au temps \(t\) \((x=c~t)\), alors que la voiture la reçoit au temps \(t'\) \((x'=c~t')\).
Or, on a : \(x'\neq x \Rightarrow t'\neq t\).
D’où le principe d’équivalence : \[c^2~t^2-x^2=0\quad;\quad c'^2~t'^2-x'^2=0\]
Si on remplace l’étincelle par une détonation (la vitesse de propagation n’est plus une constante) : \[x=v~t\quad;\quad x'=v'~t'\quad;\quad v\ll c\quad;\quad v'\ll c\]
Par suite : \[c^2~t^2-x^2>0\quad;\quad c'^2~t'^2-x'^2>0\]
Si, pour un référentiel, la quantité \(c^2~t^2-x^2\) est nulle, la quantité \(c^2~t'^2-x'^2\) associée à l’autre référentiel est également nulle. On montrerait de même que la condition \(c^2~t^2-x^2>0\) entrainerait \(c^2~t'^2-x'^2>0\) et réciproquement.
Pour les deux systèmes galiléens, les quantités \(s^2=c^2~t^2-x^2\) et \(s'^2=c^2~t'^2-x'^2\) sont soit simultanément nulles, soit simultanément positives. Il s’ensuit que \(s'^2\) et \(s^2\) sont proportionnelles : \(s^2=k^2~s^2\). Et comme les deux référentiels jouent le même rôle, on doit avoir nécessairement \(k^2=1\).
Ainsi, lorsqu’on passe d’un repère galiléen à un autre repère galiléen, le temps n’est pas invariant. Par contre : \[s^2=c^2~t^2-x^2\quad\text{reste inchangée.}\]
C’est un invariant pour tous les systèmes galiléens.
3. Formules de transformation
On part de la relation : \[c^2~t^2-x^2=c'^2~t'^2-x'^2\]
Posant \(u=i~c~t\) et \(u'=i~c'~t'\), alors : \[x^2+u^2=x'^2+u'^2\]
Le carré de la norme du vecteur étant conservé, la transformation est une rotation. De sorte que l’on peut poser : \[\left\{ \begin{aligned} x'&=x~\cos\phi+u~\sin\phi &&x,~x'\in \mathbb R\quad;\quad\cos\phi \in \mathbb R \\ u'&=-x\sin\phi+u\cos\phi\qquad &&u\in \mathbb C\quad;\quad\sin\phi \in \mathbb C\quad;\quad\tan \phi=i~\beta\in \mathbb C \end{aligned} \right.\]
On peut écrire : \[\sin\phi=\frac{i~\beta}{\sqrt{1-\beta^2}}\quad;\quad\cos\phi=\frac{1}{\sqrt{1-\beta^2}}\]
D’où :
\[\begin{aligned} &x'=\frac{x+i~u~\beta}{\sqrt{1-\beta^2}} &&u'=\frac{-x~i~\beta+u}{\sqrt{1-\beta^2}} \\ &x'=\frac{-x~i~\beta+u}{\sqrt{1-\beta^2}} &&u'=i~c~t'=\frac{-x~i~\beta}{\sqrt{1-\beta^2}}\end{aligned}\]
Par suite : \[t'=\frac{t-x~\beta/c}{\sqrt{1-\beta^2}}\]
Quelle est la signfication physique du paramètre \(\beta\) ?
\(O'\) est animé d’une vitesse \(v\) par rapport à \(O\) \((x=v~t)\), mais dans le repère \(G'\), \(O'\) a une abscisse nulle \((x'=0)\).
Il s’ensuit que : \[v~t-\beta~c~t = 0\quad\rightarrow\quad\beta=\frac{v}{c}\]
D’où les formules (directes) de Lorentz (transformation réduite) : \[x'=\frac{x-v~t}{\sqrt{1-\beta^2}}\quad;\quad y'=y\quad;\quad z'=z\quad;\quad t'=\frac{t-v~x/c^2}{\sqrt{1-\beta^2}}\]
On retrouve les formules du repère galiléen en faisant \(c \rightarrow \infty \). Mais ceci voudrait dire qu’en mécanique classique certains objets se déplaceraient à une vitesse infinie. Par voie de conséquence, on saurait à chaque instant tout ce qui se passe dans l’univers.
La vitesse de la lumière est bien une vitesse limite. Cependant, une autre vitesse risque fort de la supplanter, celle de la gravitation qui conduit à la relativité généralisée (Einstein, 1917).
On obtient les formules de transformation inverse en opérant le changement \(v \rightarrow -v\) : \[x=\frac{x'-v~t}{\sqrt{1-\beta^2}}\quad;\quad y=y'\quad;\quad z=z'\quad;\quad t=\frac{t'-v~x'/c^2}{\sqrt{1-\beta^2}}\]
4. Conséquences des formules de Lorentz
Trois conséquences sont immédiates : ce que l’on appelle les paradoxes, la notion de temps propre et la loi de composition des vitesses.
4.1. Paradoxe de la contraction des longueurs
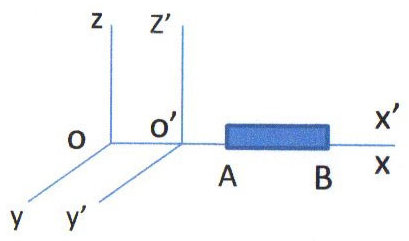Le premier paradoxe connu est celui de la contraction des longueurs. \(R\) est un repère fixe devant lequel passe une règle \(AB\) de longueur \(L\). En fonction du repère :
\[\begin{aligned} &/R:~\quad L = x_B - x_A \\ &/R':\quad L' = x'_B - x'_A\end{aligned}\]
Posons \(\alpha=\sqrt{1-\beta^2}\) et appliquons les formules de Lorentz dans \(R\) : \[x'_A = \frac{x_A-v~t}{\alpha}\quad;\quad x'_B = \frac{x_B-v~t}{\alpha}\]
d’où : \[x'_B-x'_A = \frac{x_B-x_A}{\alpha}\qquad\Rightarrow\qquad L = \alpha~L'\quad;\quad L<L'\]
Ce qui signifie qu’un observateur, immobile dans \(R\), verrait passer une règle dont la longueur se contracterait. Il en serait de même si lui-même était mobile et la règle fixe. Par exemple, la vache qui dans son pré regarderait passer un train à une vitesse proche de celle de la lumière le verrait presque totalement aplati dans le sens de la largeur. Le voyageur qui, de la fenêtre de son wagon, observerait cette vache la verrait à son tour totalement aplatie.
4.2. Paradoxe de la dilatation du temps
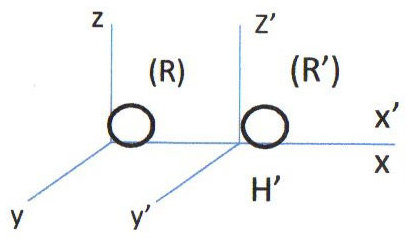Les deux horloges sont synchronisées au passage en \(O\) des deux repères. Chaque système a son temps propre à partir de cet instant. On peut écrire : \[x'=0\quad;\quad t'=\frac{t}{\alpha}\qquad\text{donc~:}\quad t < t'\]
Il y a donc une dilatation du temps, donc d’un ralentissement apparent dans le repère \(R'\) par rapport à \(R\). D’où le paradoxe du voyageur de Langevin. Ce voyageur qui quitterait la Terre à une vitesse proche de celle de la lumière aurait vieilli de deux ans alors que la Terre aurait vieilli de cinquante ans.
Ce deuxième paradoxe a d’ailleurs pu être vérifié expérimentalement. Une particule élémentaire, le muon \(\mu\), produit par les rayons cosmiques se forme à 15 km d’altitude. Au bout d’un certain temps de l’ordre de \(\tau \approx\) 2,2 µs, il est transformé en un électron et un neutrino. À cette durée correspond une longueur de vie de l’ordre de : \[L=3.10^8 \times 2,2 \times 10^{-6}~\rm m=660~\rm m\]
On retrouve cependant ces particules sur la Terre. En effet, pour l’observateur terrestre, la durée de vie est de \( T= \tau / \alpha \), donc \(T>\tau\).
4.3. Notion de temps propre
Le temps propre \(\tau\) est le temps donné par une horloge au repos par rapport au système galiléen auquel on l’attache : c’est le temps (minimal) transporté avec soi. \[t=\frac{t'}{\sqrt{1-\beta^2}} = \frac{t'}{\alpha}\quad\Rightarrow\quad\tau=t'=\alpha~t\]
On sait que : \[s^2=c^2~t^2-x^2\]
C’est un invariant quand on change de repère galiléen :
\[\begin{aligned} &s^2=c^2~t^2-v^2~t^2=c^2~\Big(1-\frac{v^2}{c^2}\Big)~t^2 \\ &s^2=c^2~\alpha^2~t^2=c^2~\tau^2\qquad\Rightarrow\qquad s=c~\tau\end{aligned}\]
Il s’ensuit que le temps propre est un invariant dans un changement de repère galiléen.
4.4. Loi de composition des vitesses
Considérons le mouvement du point \(M\). Ce point est animé d’une vitesse \(u\) dans \(R\) et d’une vitesse \(u'\) dans \(R'\). \(R'\) se déplace à une vitesse \(v\) par rapport à \(R\). On écrirait, en mécanique classique (\(t'=t\)) : \[x'=x-v~t\quad\Rightarrow\quad\frac{dx'}{dt}=\frac{dx}{dt}-v\]
C’est-à-dire : \[u'=u-v\quad\text{et}\quad u=u'+v\]
En mécanique relativiste :
\[\begin{aligned} x'=\frac{x-v~t}{\alpha}\quad&\Rightarrow\quad dx'=\frac{dx-v\ dt}{\alpha}\\ t'=\frac{t-v~x/c^2}{\alpha}\quad&\Rightarrow\quad dt'=\frac{dt-(v/c^2)~dx}{\alpha}\end{aligned}\]
On a donc : \[\frac{dx'}{dt'}=\frac{\cfrac{dx}{dt}-v}{1-\cfrac{v}{c^2}~\cfrac{dx}{dt}}\]
Cette dernière formule montre que, si prend \(u'=c\), on obtient \(u=c\). Ceci confirme que la célérité de la lumière \(c\) est une constante pour tout repère galiléen.
5. Expérience de Fizeau
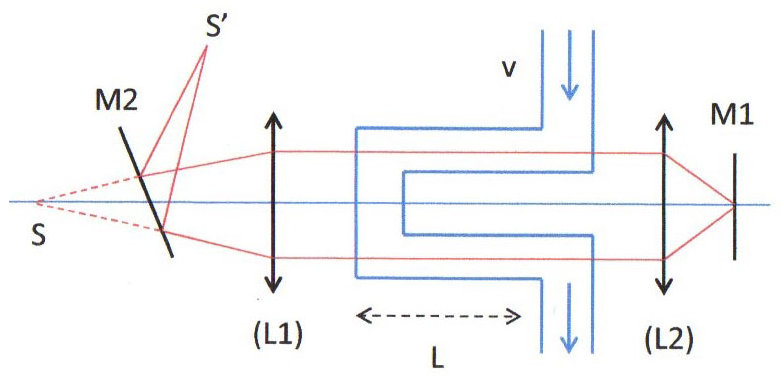Un courant d’eau régulier (vitesse \(v\) de l’ordre de 10 m/s) est maintenu dans le tube. La lumière issue de \(S\) effectue un aller-retour dans chaque branche, une fois avec le courant et l’autre à contre-courant.
\(L_1\) et \(L_2\) sont des lentilles convergentes. Le miroir sans tain \(M_2\) permet de retrouver les rayons concentrés en \(S'\).
Fizeau y observait des interférences et expliquait l’expérience en suivant le raisonnement de la mécanique classique. L’eau transportant le rayon lumineux, il y a donc deux vitesses possibles pour ces rayons : \[u=\frac{c}{n}\pm v\]
Calculons la différence de marche des trajets lumineux. Elle engendre des franges d’interférences : \[\Delta t=\frac{L}{\cfrac{c}{n}-v}-\frac{L}{\cfrac{c}{n}+v}\thickapprox \frac{2~L~n^2}{c} \quad\rightarrow\quad \Delta L = 2~L~n^2~\beta = c~\Delta t\]
Numériquement : \[L=10~{\rm m}\quad;\quad n=\frac{4}{3}\quad;\quad v=10~{\rm m/s}\quad;\quad \Delta L=\frac{32}{27}~{\rm\mu m}\]
Mais en mécanique relativiste : \[u=\frac{\cfrac{c}{n}-v}{1-\cfrac{c~v}{n~c^2}}\quad;\quad u=\frac{\cfrac{c}{n}+v}{1+\cfrac{c~v}{n~c^2}}\]
Par suite : \[\Delta t=\frac{L}{u}-\frac{L}{u'}=2~L~n^2~\beta~\Big(1-\frac{1}{n^2}\Big)\]
Ce dernier facteur étant de l’ordre de \(1/2\), l’interfrange correspondant est la moitié de celle obtenue précédemment.
Fizeau avait effectivement obtenu ce résultat expérimental qui différait du calcul effectué en mécanique classique, mais il l’expliquait de manière empirique en prétendant qu’il fallait corriger la formule et il posait à priori : \[u=\frac{c}{n}+v\qquad\rightarrow\qquad u'=\frac{c}{n}+v~\Big(1-\frac{1}{n^2}\Big)\]
