1. Vecteur impulsion relativiste
On rappelle l’expression des composantes du vecteur vitesse : \[\lambda^0=\frac{1}{\alpha}\quad;\quad\lambda^i=\frac{1}{\alpha~c}v^i~~,\quad i=1,~2,~3\]
On désigne par \(m_0\) la masse au repos de la particule (donc dans son repère propre).
Le vecteur impulsion est défini par :
\[\begin{aligned} P^{\alpha}&=m_0~c~\lambda^{\alpha}~~,\quad\alpha=0,~1,~2,~3~~\text{(4 dimensions)} \\ P^i&=m~v^i\quad\text{avec :}~~m=\frac{m_0}{\sqrt{1-\beta^2}} \\ P^0&=m_0~c~\lambda^0=\frac{m_0~c}{\alpha}=m~c=\frac{m~c^2}{c}\quad\text{(énergie/c) ou (eV/c)} \\ {(P)}^2&=P_{\alpha}~P^{\beta}=(P^0)^2-\sum_{i=1}^{i=3}(P^i)^2=m^2~c^2-m^2~v^2=m^2~c^2~\alpha^2=m_0^2~c^2 \\ {(P)}^2 &= m_0~c~\lambda^\alpha~.~m_0~c~\lambda_\alpha = m_0^2~c^2~\lambda^\alpha~\lambda_\alpha = m_0^2~c^2\end{aligned}\]
En résumé : \[P^0=m~c\quad;\quad P^i=m~v^i\quad;\quad(P)^2=m_0^2~c^2\quad\text{avec :}~~m=\frac{m_0}{\sqrt{1-\beta^2}}\]
2. Formule fondamentale de la dynamique
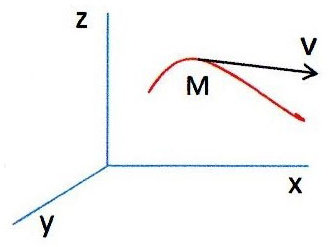 Considérons un quadrivecteur \(\overrightarrow{F}\).
Considérons un quadrivecteur \(\overrightarrow{F}\).
En mécanique classique : \[\overrightarrow{F}=\frac{d}{dt}(m~\overrightarrow{v})=\frac{\overrightarrow{dP}}{dt}\qquad\text{(3 équations)}\]
En relativité restreinte : \[\overrightarrow{F}=\frac{\overrightarrow{dP}}{d\tau}\qquad\text{(4 équations)}\]
Pour des vitesses faibles, trois équations sur quatre redonnent les résultats de la mécanique classique (en faisant \(c \rightarrow \infty\)) :
\[F^i=\frac{dP^i}{d\tau}=\frac{d}{d\tau}(m_0~c~\lambda^i)=m_0~c~\frac{d\lambda^i}{d\tau}=m_0~c~\frac{d}{d\tau}\Big(\frac{v^i}{\alpha~c}\Big)\]
\(\tau\) est le temps propre : \[F^i=m_0~c~\frac{d}{dt}\Big(\frac{v^i}{\alpha~c}\Big)~\frac{dt}{d\tau}\]
Or, on sait que : \[\frac{dt}{d\tau}=\frac{1}{\alpha}\]
Le calcul peut être refait brièvement d’une autre manière : \[ds^2=c^2~t^2-dx^2-dy^2-dz^2=(c^2-v^2)~dt^2=c^2~\alpha^2~dt^2=c^2~d\tau^2\]
On a donc : \[F^i=\frac{m_0~c}{\alpha}~\frac{d}{dt}\Big(\frac{v^i}{\alpha~c}\Big) \quad\text{ou }\quad \alpha~\overrightarrow{F^i}=\frac{d}{dt}\Big(\frac{m_0~v^i}{\alpha}\Big)\]
Faisant \(\alpha \thickapprox 1\), on retrouve les résultats de la mécanique classique.
Remarque : \(m_0\) est la masse de la particule dans son repère propre ; c’est encore la masse au repos. Par contre, pour le repère \(Oxyz\) par rapport auquel cette particule se déplace, on devra prendre \(m=m_0/\alpha\). La masse a donc perdu son caractère absolu.
3. Interprétation physique de la quatrième dimension
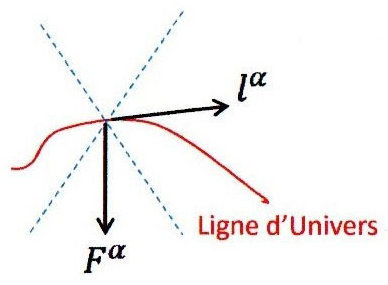 Reprenons l’expression de la force :
Reprenons l’expression de la force :
\[\begin{aligned} F^0&=\frac{dP^0}{d\tau}=\frac{d}{d\tau}\Big(\frac{m_0~c}{\alpha}\Big)= \frac{d}{dt}\Big(\frac{m_0~c}{\alpha}\Big)~\frac{dt}{d\tau}= \frac{m_0~c}{\alpha}.\frac{d}{dt}\Big(\frac{1}{\alpha}\Big) \\ F^{\alpha}&=\frac{dP^{\alpha}}{d\tau}=m_0~c~\frac{d\lambda^{\alpha}}{d\tau}=m_0~c~\Gamma^{\alpha}\end{aligned}\]
\(\lambda^{\alpha}\) étant un vecteur temporel et \(F^{\alpha}\) étant un vecteur spatial : \[\lambda^{\alpha}~\Gamma_{\alpha}=0\quad\Rightarrow\quad\lambda_{\alpha}~F^{\alpha}=0\]
En exploitant cette propriété : \[F^0~\lambda_0 + F^1~\lambda_1 + F^2~\lambda_2 + F^3~\lambda_3=0\quad\text{ou}\quad F^0~\lambda^0 = F^1~\lambda^1 + F^2~\lambda^2 + F^3~\lambda^3\]
\[\frac{m_0~c}{\alpha}~\frac{d}{dt}\Big(\frac{1}{\alpha}\Big)= \sum_{i=1}^{i=3}F^i~\lambda^i=\sum_{i=1}^{i=3}F^i~\frac{v^i}{\alpha c}\qquad\text{soit :}\quad \frac{d}{dt}\Big(\frac{m_0~c^2}{\alpha}\Big)=\sum_{i=1}^{i=3}F^i~v^i=\overrightarrow{F}\cdot\overrightarrow{V}\]
On a donc : \[d(m~c^2)=(\overrightarrow{F}\cdot\overrightarrow{V})~dt=\overrightarrow{F}\cdot\overrightarrow{ds}=dW\]
C’est le travail de la force appliquée.
Si l’on suppose que les forces dérivent d’un potentiel \(\Phi\), c’est-à-dire \(dW=-d\Phi\) : \[d(m~c^2)+d\Phi=0\quad\Rightarrow\quad m~c^2+\Phi=cte=E\]
\(E\) est l’énergie cinétique relativiste de la particule pour l’observateur. Elle exprime le théorème de conservation de l’énergie en relativité générale. Elle est liée au repère galiléen de l’observateur : \[E=\frac{m_0}{\sqrt{1-\beta^2}}~c^2+\Phi\]
qui peut s’écrire : \[E=m_0~c^2~(1-\beta^2)^{-1/2}+\Phi\]
En introduisant un développement limité : \[E\thickapprox m_0~c^2+\frac{m_0~v^2}{2}+\dots+ \Phi\]
Aux vitesses faibles, les deux derniers termes représentent respectivement une énergie cinétique et une énergie potentielle. On ne retrouve donc pas le théorème de l’énergie cinétique (présence du terme \(m_0~c^2\)).
En mécanique classique, une particule au repos (pas d’énergie potentielle) n’a pas d’énergie. Par contre, en mécanique relativiste, elle possède une énergie \(E=m_0~c^2\). Il y a donc équivalence entre la masse et l’énergie ; celle-ci peut se matérialiser.
Équivalence d’énergie de 1 kg d’eau = \(1\times(3\times10^8)^2=9\times 10^{16}~\rm J\thickapprox\) 30 milliards de kW\(\cdot\)h.
4. Impulsion d’une particule
On peut écrire : \[E=E_{masse}+\Phi_{potentiel}\]
Pour l’impulsion spatiale : \[P^i=\frac{m_0~v^i}{\alpha}=m~v^i\]
Pour l’impulsion temporelle :
\[\begin{aligned} P^0&=\frac{m_0~c}{\alpha}=m~c=\frac{m~c^2}{c}=\frac{E}{c} \\ {(P)}^2&=m_0^2~c^2=(P^0)^2-\sum_{i=1}^{i=3}(P^i)^2=\frac{E^2}{c^2}-\sum_{i=1}^{i=3}(P^i)^2\end{aligned}\]
D’où l’on tire : \[E^2=m_0^2~c^4+c^2~\sum_{i=1}^{i=3}(P^i)^2\]

