1. Action d’une force constante sur une particule

En mécanique classique, le mouvement d’une particule sous l’action d’une force constante est un mouvement uniformément accéléré : \[v=\gamma~t + v_0\]

On serait tenté de dire que \(v \rightarrow \infty\) quand \(t \rightarrow \infty\).

Dans le contexte relativiste : \[\frac{d}{dt}\Big(\frac{m_0~v}{\sqrt{1-v^2/c^2}}\Big)=f\quad\Rightarrow\quad \dfrac{m_0~v}{\sqrt{1-v^2/c^2}}=f~t+cte\]

Si on suppose la vitesse nulle à l’instant initial, toujours par rapport à un repère galiléen, alors la constante est nulle : \[\frac{m_0^2~v^2}{1-v^2/c^2}=f^2~t^2\quad\Rightarrow\quad \frac{v^2}{c^2}=\frac{f^2~t^2-m_0^2~v^2}{f^2~t^2}\] \[\beta=\frac{v}{c}=\frac{\sqrt{f^2~t^2-m_0^2~v^2}}{f~t}\]

On constate que, lorsque le temps devient infini, \(\beta\rightarrow 1\), donc la vitesse de la particule tend vers la vitesse de la lumière qui est bien une vitesse limite.

2. Mouvement d’un électron dans un champ magnétique

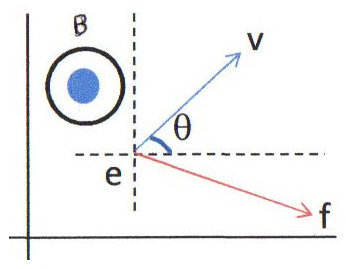En mécanique classique : \[\overrightarrow{f}=e~\overrightarrow{V}\times\overrightarrow{B}\quad;\quad\overrightarrow{f}\perp\overrightarrow{V}\]

Accélération centrale : \[\gamma=\frac{v^2}{R}=\frac{f}{m}\]

La particule décrit un cercle de rayon \(R\) : \[R=\frac{m~v}{e~B}\]

En relativité, nous pouvons anticiper en écrivant que \(\overrightarrow{f}=e\overrightarrow{V}\times\overrightarrow{B}\) en supposant par ailleurs que \((\overrightarrow{ox},~\overrightarrow{V})=\theta\)   à l’origine.

On part des relations : \[\overrightarrow{f}=\frac{d}{dt}(m~\overrightarrow{V})\quad;\quad m=\frac{m_0}{\sqrt{1-v^2/c^2}}\]

En projection sur les axes \(\overrightarrow{Ox}\) et \(\overrightarrow{Oy}\) :

\[\begin{aligned} \frac{d}{dt}\Big(\frac{m_0~v}{\sqrt{1-v^2/c^2}}\Big)~\cos\theta &=e~v~B\sin\theta &&(1) \\ \frac{d}{dt}\Big(\frac{m_0~v}{\sqrt{1-v^2/c^2}}\Big)~\sin\theta &=-e~v~B\cos\theta&&(2)\end{aligned}\]

En multipliant les deux relations par les expressions à droite respectivement par \(\cfrac{2~v~\cos\theta}{\sqrt{1-v^2/c^2}}\) et par \(\cfrac{2~v~\sin\theta}{\sqrt{1-v^2/c^2}}\) , puis en additionnant : \[m_0~\frac{d}{dt}\Big(\frac{v^2~\cos^2\theta}{1-v^2/c^2}\Big) + m_0~\frac{d}{dt}\Big(\frac{v^2~\sin^2\theta}{1-v^2/c^2}\Big)=0\]

C’est-à-dire : \[\frac{d}{dt}\Big(\frac{v^2}{\sqrt{1-v^2/c^2}}\Big)=0\quad\Rightarrow\quad v=constante\]

La relation (1) peut s’écrire : \[\frac{m_0~v~\sin\theta}{\sqrt{1-v^2/c^2}}~\frac{d\theta}{dt}=-e~v~B~\sin\theta\]

D’où : \[\frac{d\theta}{dt}=-\frac{e~B}{m_0}~\sqrt{1-v^2/c^2}=constante\]

En intégrant sur une période de révolution : \[2\pi=-\frac{e~B}{m_0}\sqrt{1-v^2/c^2}~~T=-\frac{e~B}{m_0}\sqrt{1-v^2/c^2}~~\frac{2\pi~R}{v}\] \[-\frac{e}{m_0}=\frac{v}{R~B}~\sqrt{1-v^2/c^2}\]

Cette formule peut être vérifiée expérimentalement. L’expérience, réalisée par Guye et Lavanchy tendant à vérifier la relation aux masses a été faite sur un spectromètre de masse.

3. Cas du photon

Le photon est une particule bizarre : comme sa vitesse est \(v = c\), on serait tenté de dire que sa masse est infinie. Le photon n’existe pas au repos quelque soit le système de référence et sa vitesse est toujours égale à \(c\).

Depuis l’énoncé de la théorie de la relativité d’Einstein, on sait que son énergie est \(E=h~\nu\), \(h\) étant la constante de Planck et \(\nu\) la fréquence de la radiation émise.

Bien que le photon soit sans masse, il est possible de considérer une quantité de mouvement \(\overrightarrow{P}\) exprimée au moyen d’une masse. En fait \(\overrightarrow{P}\) a une longueur nulle : \[(P^0)^2-(P^1)^2-(P^2)^2-(P^3)^2=0\]

Et on sait que : \[P^0=m~c=\frac{E}{c}=\frac{h~\nu}{c}\]

Dans un espace ordinaire : \[P^1=k~e^1\quad;\quad P^2=k~e^2\quad;\quad P^3=ke^3\] \[(e^1)^2+(e^2)^2+(e^3)^2=1\qquad\text{ cosinus directeurs}\]

Dans l’espace-temps : \[(P^0)^2=\Big(\frac{h~\nu}{c}\Big)^2=k^2~(e^1)^2+k^2~(e^2)^2+k^2~(e^3)^2=k^2 \quad\Rightarrow\quad k=\frac{h~\nu}{c}\]

Donc, pour un photon : \[P^0=\frac{h~\nu}{c}\quad;\quad P^i=\frac{h~\nu}{c }~e^i\]

D’une manière générale, une particule traditionnelle : \[\mid \overrightarrow{P} \mid=m_0~c\]

Comme dans le cas de la lumière, le vecteur est isotrope, on aura : \[\mid \overrightarrow{P} \mid=0\]

C’est-à-dire que l’on doit supposer dans ce cas que \(m_0=0\).

4. Collisions de particules

Dans un choc de particules, l’équation fondamentale est basée sur le principe de conservation de la quantité de mouvement : \[P^\alpha \rightarrow P^{\alpha'} \ \ \ \Rightarrow \ \ \ \sum P^{\alpha} = \sum P^{\alpha'}\]

Dans l’espace-temps :

\[\begin{aligned} \sum{\frac{m_0~c}{\alpha}}+\sum{\frac{h~\nu}{c}} &= \sum{\frac{m'_0~c}{\alpha'}}+\sum{\frac{h~\nu'}{c}} \\ \sum{\frac{m_0~v^i}{\alpha}}+\sum{\frac{h~\nu}{c}}~e^i&=\sum{\frac{m_0~v'^i}{\alpha}} + \sum{\frac{h~\nu'}{c}}~e'^i\quad\quad i=1,~2,~3\end{aligned}\]

Pour simplifier, nous considèrerons le cas de deux particules en partant du lemme suivant :

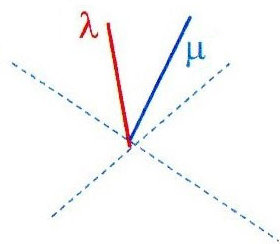
Soit deux vecteurs unitaires \(\overrightarrow{\lambda}\) et \(\overrightarrow{\mu}\) dirigés vers le futur. Leur produit scalaire est tel que \(\overrightarrow{\lambda}\cdot\overrightarrow{\mu}\geq 1\)

Prenons maintenant un repère \((\overrightarrow{e_0},~\overrightarrow{e_1},~\overrightarrow{e_2},~\overrightarrow{e_3})\) tel que \(\overrightarrow{e_0}=\overrightarrow{\lambda}\). On a donc : \[\overrightarrow{\lambda}(1,~0,~0,~0)~~\text{et}~~\overrightarrow{\mu}(\mu^0,~\mu^1,~\mu^2,~\mu^3)\] \[(\mu^0)^2-(\mu^1)^2-(\mu^2)^2-(\mu^3)^2=1\quad\Rightarrow\quad\mu^0 \geq 1\] \[\overrightarrow{\lambda}\cdot\overrightarrow{\mu} = \mu^0\quad\Rightarrow\quad \overrightarrow{\lambda}\cdot\overrightarrow{\mu} \geq 1\]

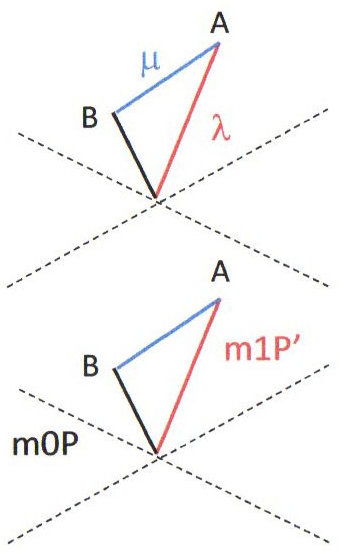Que devient alors l’inégalité triangulaire ? Nous allons démontrer que \(\overrightarrow{OB}\geq\overrightarrow{OA}+\overrightarrow{AB}\) : \[\overrightarrow{OA}=OA~\overrightarrow{\lambda}\quad;\quad\overrightarrow{AB}=AB~\overrightarrow{\mu}\quad;\quad \overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}\] \[\overline{OB^2}=\overline{OA^2}+\overline{AB^2}+2~\overrightarrow{OA}\cdot\overrightarrow{AB}= \overline{OA^2}+\overline{AB^2}+2~\overline{OA}~\overline{AB}~(\overrightarrow{\lambda}\cdot\overrightarrow{\mu})\]

Conséquence physique : en transposant l’écriture précédente à celle de particules, il vient : \[\overrightarrow{P}\rightarrow\overrightarrow{P'}+\overrightarrow{P''}\quad\text{et}\quad m_0>m_1+m_2\]

La différence de masse a disparue sous forme d’énergie.

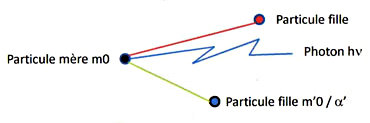Considérons à présent une particule \(m_0\) qui se désintègre pour donner des particules et des photons. En prenant le système propre de la particule au repos, on aura (équation de désintégration) :

\[\begin{aligned} m_0~c&=\sum{\frac{m'_0~c}{\alpha'}}+\sum{\frac{h~\nu}{c}} \\ m_0~c&=\sum{\frac{m'_0~c}{\alpha'}}+\sum{h~\nu'}\end{aligned}\]

Bilan énergétique de la réaction nucléaire : \[Q=m_0~c^2-\sum{m'_0~c^2}=(m_0-\sum{m'_0})~c^2=\Delta m~c^2\]

\(Q > 0\) : Il lui correspond une particule instable.

\(Q < 0\) : Il lui correspond une particule stable.