1. Bases de la trajectographie

Les bases de la trajectographie sont fondées sur la réfraction des ondes électromagnétiques par l’ionosphère, la technique de base reposant toujours sur le principe de Fermat et les lois de Descartes. Pour simplifier l’exposé, nous pouvons faire l’hypothèse d’un milieu de propagation régulièrement stratifié.

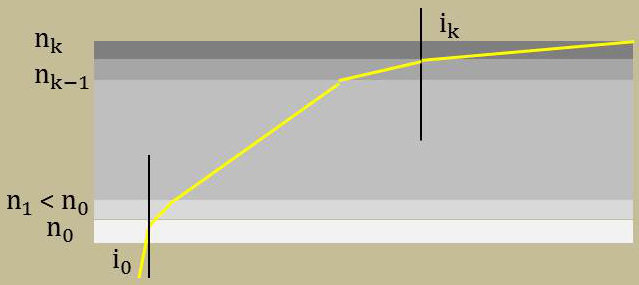D’après les lois de Descartes : \[n_0~\sin(i_0)~=~\dots~=~n_k~\sin(n_k)~=~cte\]

Il n’y a retour du rayon sur la Terre que s’il y a réflexion totale : \[i_k=\frac{\pi}{2}\]

On a alors : \[n_k=\sin(i_0)=\sqrt{1-\Big(\frac{f_p}{f}\Big)^2}\qquad\Rightarrow\qquad~f=\frac{f_p}{\cos(i_0)}\]

En sondage zénithal de l’ionosphère : \[i_0=0\qquad\Rightarrow\qquad f_z=f_p\]

En sondage oblique de l’ionosphère : \[i_0\neq 0\qquad\Rightarrow\qquad f_0=\frac{f_p}{\cos(i_0)}>f_p\]

1.1. Théorème de Breit et Tuve

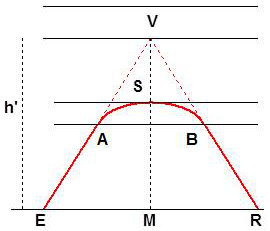Le temps de propagation de groupe de la trajectoire réelle est égal au temps de parcours du trajet \(EVR\) à la vitesse de la lumière.

Le point \(V\) est l’image virtuelle du point \(S\) vue du sol.

Le trajet \(EVR\) est dit virtuel ; l’altitude du point \(V\) est appelée hauteur virtuelle de réflexion et notée \(h'\).

Autrement dit, le temps de propagation de groupe du trajet virtuel est égal au temps de propagation de groupe du trajet réel.

1.2. Théorème de Martyn

On considère deux ondes, l’une oblique et l’autre verticale, se réfléchissant à la même hauteur S. Leurs fréquences vérifient la loi de sécante.

Par application du théorème de Breit et Tuve, le théorème de Martyn démontre que si deux ondes se réfléchissent à la même altitude, elles ont même hauteur virtuelle de réflexion et leur temps de groupe est lié par la relation au temps de groupe en incidence normale. \[T_{gv}=T_g~\cos(i_0)\]

2. Calcul des trajectoires ionosphériques

Dans le cas général, le calcul de la propagation d’une onde dans l’ionosphère est relativement compliqué. Toutefois, lorsque la fréquence d’émission dépasse quelques mégahertz et dans la mesure où l’indice varie peu sur une distance de l’ordre de la longueur d’onde, ce qui revient à considérer le milieu comme localement homogène, on démontre qu’il est possible de traiter le problème suivant les principes de l’optique géométrique.

Dans cette hypothèse, la propagation s’effectue le long du rayon qui représente la trajectoire de l’énergie et qui est tangent en tout point au vecteur de Poynting. Quand le champ magnétique n’est pas nul, le rayon ne coïncide pas avec la direction de propagation des surfaces équiphases et le calcul de la trajectoire est relativement compliqué. Des méthodes existent cependant, nécessitant de longs calculs sur ordinateur.

2.1. Principe mathématique. Équations hamiltoniennes

Une méthode intéressante pour calculer la trajectoire de l’onde est celle développée par Haselgrove. Il s’agit d’une application des équations hamiltoniennes au tracé des rayons dans un milieu anisotrope. Elle a été développée pour les applications sur ordinateur et décrit la trajectoire par un système d’équations différentielles du premier ordre.

Un point courant de la trajectoire est défini par ses coordonnées (\(x_1,~x_2,~x_3\))et par un vecteur de propagation \(\overrightarrow{p}\) dont les composantes sont (\(p_1,~p_2,~p_3\)). La longueur de \(\overrightarrow{p}\) est égale à l’indice de réfraction \(n\) en ce point et pour cette direction de propagation (normale à l’onde) : \[p=\sqrt{p_1^2+p_2^2+p_3^2}=n\]

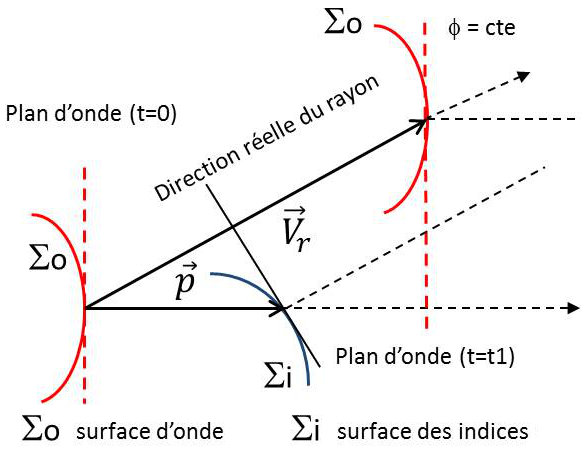Les équations sont exprimées en fonction d’une quantité scalaire G définie par : \[G=\frac{\sqrt{p_1^2+p_2^2+p_3^2}}{n(x_1,x_2,x_3~;~p_1,p_2,p_3)}=1\]

La fonction \(G(x_1,x_2,x_3~;~p_1,p_2,p_3)\) est appelée surface des indices. L’indice \(n\) est donné par la formule d’Appleton.

On notera que si la valeur de \(G\) est égale à l’unité, ses dérivées partielles par rapport à\(xi\) et \(pi\) ne sont pas nécessairement nulles, l’indice dans le milieu anisotrope étant fonction du point et de la direction.

On vérifie d’autre part que l’indice \(n\) et la surface des indices \(G\) sont des fonctions homogènes en \(p\) d’ordres respectifs 0 et 1.

Avec ces définitions, les équations hamiltoniennes de la trajectoire s’écrivent : \[\left\{ \begin{aligned} &\frac{dx_i}{dt}=c~\frac{\partial G}{\partial p_i}\\ &\frac{dp_i}{dt}=-c~\frac{\partial G}{\partial x_i} \end{aligned} \right.\qquad i=1,~2,~3\]

• \(c\) est la vitesse de la lumière ;

• \(t\) est une variable indépendante fonction du temps le long de la trajectoire.

Ces équations sont les équations canoniques de la trajectoire. Elles ressemblent aux équations canoniques de Hamilton en dynamique et constituent une sorte de généralisation de la loi de Descartes.

2.2. Expressions analytiques des équations hamitoniennes

En pratique, il est nécessaire d’exprimer les équations de la trajectoire en coordonnées sphériques (\(r,~\theta,~\varphi\)), bien adaptées à l’étude de la propagation ionosphérique. On obtient un premier système d’équations : \[\left\{ \begin{aligned} \frac{dr}{d\tau}&=\frac{\partial G}{\partial r}\\ \frac{d\theta}{d\tau}&=\frac{1}{r}~\frac{\partial G}{\partial\theta}\\ \frac{d\varphi}{d\tau}&=\frac{1}{r~\sin(\theta)}~\frac{\partial G}{\partial\varphi}\\ \frac{\partial p_r}{d\tau}&=-\frac{\partial G}{\partial r}+\frac{1}{r}~p_{\theta}~\frac{\partial G}{\partial p_{\theta}}+\frac{1}{r}~p_{\varphi}~\frac{\partial G}{\partial p_{\varphi}}\\ \frac{\partial p_{\theta}}{d\tau}&=\frac{1}{r}~\Big\{-\frac{\partial G}{\partial\theta}-p_{\theta}~\frac{\partial G}{\partial p_r}+\operatorname{cot}(\theta)~p_{\varphi}~\frac{\partial G}{\partial p_{\varphi}}\Big\}\\ \frac{\partial p_{\theta}}{d\tau}&=\frac{1}{r~\sin\theta}~\Big\{-\frac{\partial G}{\partial\varphi}-\sin(\theta)~p_{\varphi}~\frac{\partial G}{\partial p_r}+cos(\theta)~p_{\varphi}~\frac{\partial G}{\partial p_{\theta}}\Big\} \end{aligned} \right.\]

Suivant la notation utilisée par Haselgrove, dans ces équations, les vitesses sont rapportées à la vitesse de la lumière et la variable indépendante \(\tau\) est le retard de phase équivalent qui représente en réalité le chemin de phase.

En calculant les dérivées de la fonction surface des indices par rapport aux coordonnées et par rapport aux composantes de la direction de propagation, nous obtenons les équations différentielles de la trajectoire, lesquelles ne font intervenir que l’indice de réfraction et ses dérivées. On obtient finalement : \[\left\{ \begin{aligned} \frac{dr}{d\tau}&=\frac{1}{n^2}~\Big[p_r-n~\frac{\partial n}{\partial p_r}\Big]\\ \frac{d\theta}{d\tau}&=\frac{1}{r~n^2}~\Big[p_{\theta}-n~\frac{\partial n}{\partial p_{\theta}}\Big]\\ \frac{d\varphi}{d\tau}&=\frac{1}{r~n^2~\sin(\theta)}~\Big[p_{\varphi}-n~\frac{\partial n}{\partial p_{\varphi}}\Big]\\ \frac{dp_r}{d\tau}&=\frac{1}{n}~\frac{\partial n}{\partial r}+p_{\theta}~\frac{1}{r~n^2}~\Big[p_{\theta}-n~\frac{\partial n}{\partial p_{\theta}}\Big]+p_{\varphi}~\frac{1}{r~n^2}~\Big[p_{\varphi}-n~\frac{\partial n}{\partial p_{\varphi}}\Big]\\ \frac{dp_{\theta}}{d\tau}&=\frac{1}{r}~\left\{\frac{1}{n}~\frac{\partial n}{\partial\theta}-p_{\theta}~\frac{1}{n^2}~\Big[p_r-n~\frac{\partial n}{\partial p_r}\Big]+\operatorname{cot}(\theta)~ p_{\varphi}~\frac{1}{n^2}~\Big[p_{\varphi}-n~\frac{\partial n}{\partial p_{\varphi}}\Big]\right\}\\ \frac{dp_{\theta}}{d\tau}&=\frac{1}{r~\sin\theta}~\left\{\frac{1}{n}~\frac{\partial n}{\partial\varphi}-\sin(\theta)~p_{\varphi}~\frac{1}{n^2}~\Big[p_r-n~\frac{\partial n}{\partial p_r}\Big]+\cos(\theta)~p_{\varphi}~\frac{1}{n^2}~\Big[p_{\theta}-n~\frac{\partial n}{\partial p_{\theta}}\Big]\right\} \end{aligned} \right.\]

La variable indépendante \(\tau\) est le chemin de phase. L’indice de réfaction \(n\) et ses dérivées par rapport aux trois coordonnées par rapport à la direction de propagation sont calculés par la formule d’Appleton pour un modèle ionosphérique déterminé et pour le mode de propagation choisi.

Partant d’un point connu, l’intégration des trois premières équations de la trajectoire fournit le point suivant tandis que celle des trois dernières fournit la nouvelle direction de propagation, c’est-à-dire la direction de la normale au plan d’onde.

Rappelons que, dans un milieu anisotrope, la direction de propagation, c’est-à-dire la direction de la normale au plan d’onde, est différente de la direction de propagation de l’énergie. Cette dernière est parallèle au vecteur de Poynting et est appelée direction du rayon, car elle est tangente en chaque point à la trajectoire.

2.3. Chemin de groupe et chemin de phase

Explicitons les notions de chemin de groupe et de chemin de phase.

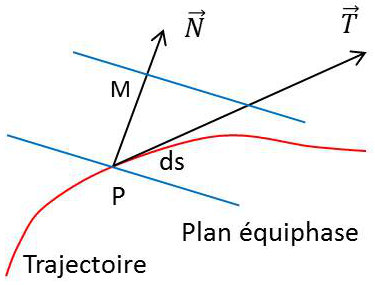Le temps de phase \(T_{\varphi}\) est le temps de parcours du trajet de propagation par un front d’onde. Le retard de phase représente le retard subi par une onde chromatique (ou porteuse pure) le long de la trajectoire.

Le chemin de phase est la distance parcourue \(P_{\varphi}\) par l’onde dans le vide pendant ce même temps \(T_{\varphi}\) : \[T_{\varphi}=\frac{1}{c}~P_{\varphi}\]

Le temps de groupe \(T_g\) est le temps de propagation de l’enveloppe d’un signal à bande étroite centré sur une porteuse \(f_0\) se propageant de l’émetteur \(E\) au récepteur \(R\) le long de la trajectoire.

Dans les applications pratiques, on a rarement affaire à des ondes monochromatiques, mais plutôt à des ondes modulées. Or, dans un milieu dispersif tel que l’ionosphère, la vitesse de propagation de l’enveloppe du signal ou vitesse de groupe est différente de la vitesse de phase. On écrira, pour le chemin de groupe : \[P_g=\int_E^R n_g~\cos(\gamma)~ds\]

• \(n_g\) : indice de réfraction de groupe

• \(\gamma\) : angle entre la normale au plan d’onde et le rayon

On aurait, pour le chemin de phase : \[P_{\varphi}=\int_E^R n~ds\]

Remarque

Comme nous l’avons noté précédemment, la variable indépendante \(\tau\) dans les équations de la trajectoire représente le chemin de phase. Il en résulte que le chemin de phase entre deux points \(A\) et \(B\) est donné par la relation : \[[P_{\varphi}]_{AB}=\int_A^B d\tau\]