1. Introduction

Quand le signal est émis sans transposition de fréquence, on dit que la transmission s’effectue en bande de base (BDB). Le codage électrique choisi sera celui qui s’adapte le mieux au support de transmission que l’on va utiliser pour la transmission.

Par exemple, en transmission numérique sur câble, les lignes métalliques utilisées sont constituées de tronçons séparés par des transformateurs ne laissant passer ni le continu, ni les fréquences basses. On a alors intérêt à utiliser, au lieu du code NRZ, un code bipolaire (dont le spectre de puissance est décalé vers les fréquences hautes) de façon à ne pas perdre d’informations.

2. Transmission d’un train numérique

On désire transmettre un train numérique : $$x(t)=\sum_ka_k~g(t-k~T)$$

2.1. Chaîne de transmission

La chaîne de transmission et la structure du récepteur optimal peuvent être représentées par la figure ci-dessous :

 

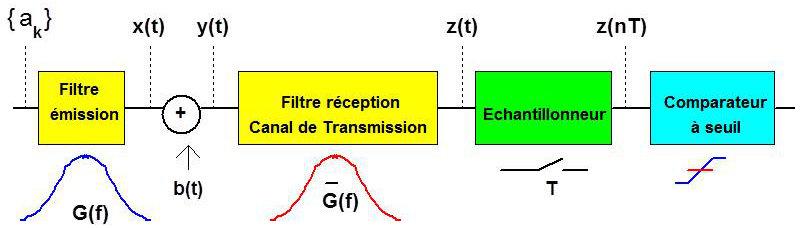
Le filtre émission, de fonction de transfert $G(f)$, est destiné à mettre en forme le train numérique.

Le bruit blanc qui vient se superposer au signal utile $x(t)$ est un bruit blanc gaussien, stationnaire et centré.

L’ensemble canal de transmission - filtre réception (ce dernier servant à éliminer le bruit en dehors de la bande utile) doit avoir pour fonction de transfert pour que la transmission soit optimale (selon la théorie de la détection).

Le signal $z(t)$ est un signal bruité par $b’(t$), résultat du filtrage de $b(t$) par l’ensemble canal de transmission - filtre réception, et qui est aussi un bruit gaussien centré.

On écrit successivement :

$$\begin{aligned} &x(t)=\sum_k a_k~g(t-k~T)\\ &y(t)=\sum_k a_k~g(t-k~T)+b(t)\\ &z(t)=y(t)\star\bar{g}(t)\qquad;\qquad\bar{g}(t)=\mathcal{F}[\bar{G}(f)]\end{aligned}$$

On obtient alors : $$z(t)=\big\{a_k~g(t-k~T)\star\bar{g}(-t)\big\}+\big\{b(t)\star\bar{g}(-t)\big\}$$

Le deuxième terme correspond au bruit filtré $b'(t)$.

Le premier terme présente une forme caractéristique quand on modifie son écriture : $$g(t-k~T)\star\bar{g}(-t)=\big\{g(t)\star\delta(t-k~T)\big\}\star\bar{g}(-t)=\big\{g(t)\star\bar{g}(-t)\big\}\star\delta(t-k~T)$$

On reconnait dans la partie entre accolades la fonction d’autocorrélation $R_{gg}$.

On a donc : $$z(t)=\sum_k a_k~R_{gg}(t-k~T)+b'(t)$$

Le signal a subi une déformation à la traversée du canal de transmission et du filtre de réception. L’information utile est à présent véhiculée par le terme : $$x(t)=\sum_k a_k~R_{gg}(t-k~T)$$

2.2. Créneau

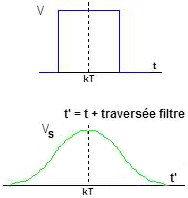Considérons l’émission d’une impulsion de la forme créneau (fonction porte).

Après traversée du filtre symbolisant le canal de transmission et le filtre réception, cette impulsion carrée pris la forme de courbe en cloche.

Il y a eu déformation (effet de traînage) due à la traversée du filtre.

2.3. Train numérique

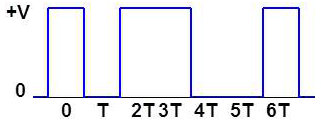On considère maintenant un train numérique: $$x(t)=\sum_k a_k~g(t-k~T)$$

Le formant est la porte d’ouverture T : $$g(t)=V~\Pi_T(t)$$

Nous allons suivre ce qui se passe au fur et à mesure de la traversée des différents organes de la chaîne de transmission.

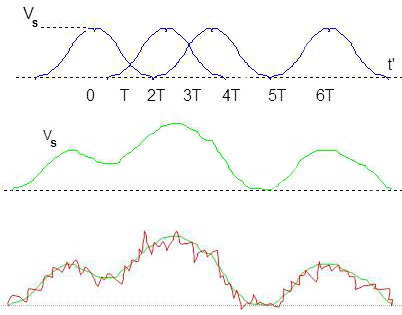Le signal reçu non bruité $z(t) - b’(t)$ aura l’allure indiquée figure ci-contre.

Le train de créneaux est devenu un train de courbes en cloche capables de chevauchement.

Compte tenu de ces chevauchements, la courbe qui en résulte fait perdre en partie du pouvoir séparateur.

Et si l’on tient compte du bruit additif sur la chaîne cette courbe est encore dégradée, mais sa forme globale est conservée du moins tant que le niveau de bruit n’est pas trop prépondérant.

À partir du signal reçu $z(t)$, il faut être en mesure de reconnaître le signal $x(t)$ émis.

Pour cela, on dispose en réception d’un échantillonneur qui viendra prélever la valeur du signal $z(t)$ tous les $kT$ aux instants où le signal a le maximum d’amplitude.

3. Interférences inter-symboles

Écrivons le signal de sortie sous la forme d’une somme de trois composantes : $$z(t)=a_k~R_{gg}(0)+\sum_{l\neq k}a_l~R_{gg}(k~T-l~T)+b'(t)$$

Le premier terme correspond à l’information recherchée $a_k$, émise à l’instant $kT$.

Le deuxième terme correspond à des perturbations dues aux réponses des impulsions adjacentes : on appelle cela de l’interférence inter-symboles ou IIS.

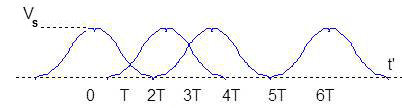Intéressons-nous à ces instants où se produisent les chevauchements et dont les additions créent une présence de signal là où il ne devrait pas y en avoir.

Par exemple, à l’instant $t’ = T$, on reçoit un certain niveau de signal (contribution des impulsions adjacentes émises aux instants $t = 0$ et $t = T$.

Pour pouvoir supprimer cette IIS qui nuit à la bonne reconnaissance du signal émis, il faut trouver le moyen de ne conserver que le terme : $$z(kT)=a_k~R_{gg}(0)+b'(kT)$$

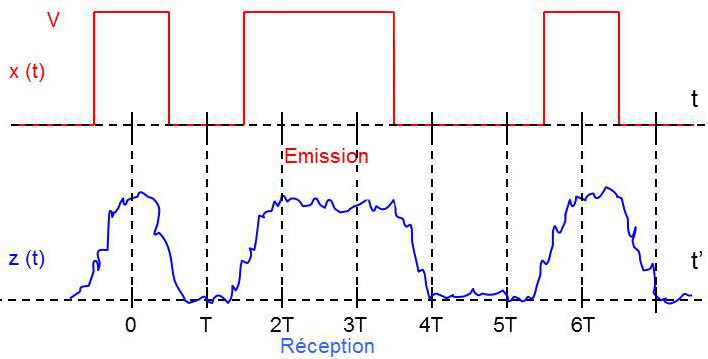Dans un système bien conçu comme celui de la figure ci-contre, on constate une reproduction correcte de la forme (malgré l’imperfection de la courbe due au bruit) ce qui fait que la détection n’en est pas affectée.

Le signal $z(t)$ est échantillonné tous les $kT$.

Le diagramme de l’œil permet d’évaluer l’instant d’échantillonnage optimal qui correspond à l’instant où l’ouverture de l’œil est maximale.

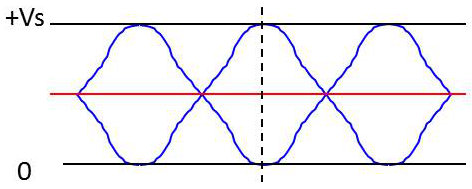Ce diagramme est obtenu en superposant toutes les formes possibles du signal $z(t)$ sur un intervalle de durée $T$. On peut l’observer physiquement à l’oscilloscope.

Une fois choisis les instants d’échantillonnage optimaux à l’aide du diagramme de l’œil, la valeur des échantillons $\{z(kT)\}_k$ est comparée à un ou plusieurs seuils selon le code utilisé.

Pour prendre l’exemple du code bipolaire d’ordre 1, on utilisera un comparateur à deux seuils $[+V_S/2,~-V_S/2]$. Tout ce qui sera détecté comme supérieur à $[+V_S/2]$ sera considéré comme +1 et tout ce qui sera détecté comme inférieur à $[-V_S/2]$ sera considéré comme -1. Tout ce qui sera détecté à un niveau compris entre $[+V_S/2]$ et $[-V_S/2]$ sera considéré comme 0.

4. Critère de Nyquist

Revenons à l’IIS. Quelle condition doit remplir $R(f)$, fonction de transfert de l’ensemble de la chaîne de transmission $T$ pour annuler cet IIS ?

Dans l’expression $z(kT)$, il faut : $$\sum_{l\neq k} a_l~R_{gg}(k~T-l~T)=0\qquad\forall \{a_l\}$$

Cela est vrai si :

$$\begin{aligned} R_{gg}(kT-lT)&=0\quad\forall~l\neq k\\ \Rightarrow\quad R_{gg}(mT)&=0\quad\forall~m\neq 0\end{aligned}$$

Tous calculs faits : $$\sum_mR(f-\frac{m}{T})=T~R_{gg}(0)$$

Cette égalité, connue sous le nom de critère de Nyquist exprime la condition que doit remplir la fonction de transfert correspondant au filtrage global de la chaîne de transmission pour qu’il n’y ait pas d’IIS.

Cette fonction de transfert, périodisée tous les $1/T$, doit être constante.

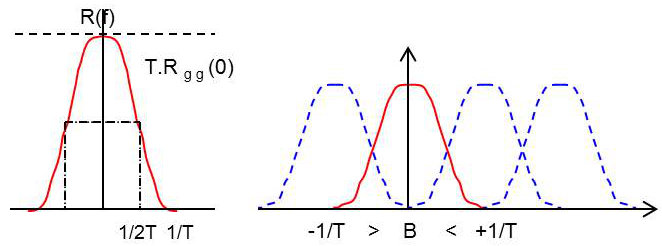Une fonction $R(f)$ symétrique par rapport au point de coordonnées : $$\left\{\frac{1}{2T}~;~\frac{T}{2}~R_{gg}(0)\right\}$$

répond exactement au critère de Nyquist.

Les filtres dits en roll off présentent une fonction de transfert de ce type. Ils correspondent à : $$\sum_mR(f-\frac{m}{T})=T~R_{gg}(0)$$

Ce critère est plus connu sous cette forme : $R_{max} = 2~B$. On voit que la rapidité de modulation et le support de transmission sont liés.

5. Calcul du taux d’erreur

Si l’interférence inter-symboles est supprimée, l’échantillonneur prélève, tous les $T$, un niveau de signal égal à : $$z(kT)=a_k~R_{gg}(0)+b'(t)$$

On désire reconnaître l’information utile $a_k$ et pour cela, on va utiliser un comparateur à seuil(s).

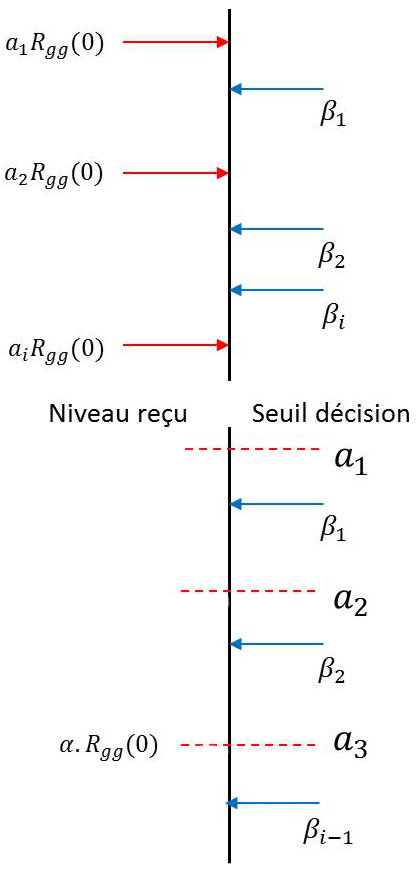
Le bruit $b'(kT)$, gaussien centré, vient perturber cette reconnaissance de $a_k$ en entraînant des risques d’erreur. S’il n’y avait pas de bruit, on aurait le schéma ci-contre et on adopterait la règle de décision suivante :

• Niveau reçu supérieur à $\beta_1$, alors $a_1$ a été émis ;

• Niveau reçu inférieur à $\beta_{i-1}$, alors $a_i$ a été émis ;

• Niveau reçu compris entre $\beta_1$ et $\beta_2$, alors $a_2$ a été émis.

En présence de bruit, les niveaux reçus ont des valeurs aléatoires. Des erreurs sont alors possibles sur l’estimation du $a_k$ émis.

On notera $\operatorname{Pr}\big[\varepsilon/a_k=a_i\big]$ la probabilité de commettre une erreur de détection, sachant que l’on a émis $ai$.

On écrira par exemple : $$\operatorname{Pr}\big[\varepsilon/a_k=a_i\big]= \operatorname{Pr}\big[b'(kT)>\frac{\alpha}{2}R_{gg}(0)\big] +\operatorname{Pr}\big[b'(kT)<-\frac{\alpha}{2}R_{gg}(0)\big]$$

Étude de cas : $b'(kT)$ gaussien centré d’écart type $\sigma’$

D’après la formule précédente qui exprime la somme de deux fonctions de répartition, on est ramené à deux calculs de surface.

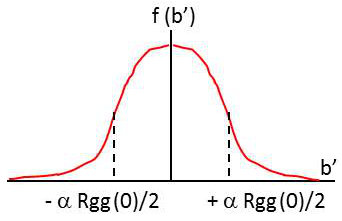Dans le cas présent, il s’agit des deux extrémités latérales délimitées par les verticales aux points d’abscisses : $$\pm\alpha~\frac{R_{gg}(0)}{2}$$

Ici, ces surfaces sont égales (symétrie de la courbe), de sorte que la probabilité d’erreur s’exprime par l’intégrale :

$$\begin{aligned} \operatorname{Pr}\big[\varepsilon/a_k=a_2\big] &= 2\int_{\lambda}^{\infty}\frac{1}{\sigma'\sqrt{2\pi}}~\exp\{-\frac{b'^2}{2\sigma'^2}\}~db'\\ \text{avec~:}\quad \lambda&=\frac{\alpha}{2}~R_{gg}(0)\end{aligned}$$

En introduisant la fonction $\operatorname{erfc}(x)$: $$\operatorname{erfc}(f)=\frac{2}{\sqrt{\pi}}\int_x^{\infty}\exp(-t^2)~dt$$

on obtiendrait : $$\operatorname{Pr}\big[\varepsilon/a_k=a_2\big] =\operatorname{erfc}\left[\frac{\alpha}{2}~\frac{R_{gg}(0)}{\sigma'~\sqrt{2}}\right]$$

On obtiendrait de la même manière : $$\operatorname{Pr}\big[\varepsilon/a_k=a_1\big]=\operatorname{Pr}\big[b'(kT)<-\frac{\alpha}{2}~R_{gg}(0)\big]$$

C’est-à-dire : $$\operatorname{Pr}\big[\varepsilon/a_k=a_1\big] =\operatorname{erfc}\left[\frac{\alpha}{2}~\frac{R_{gg}(0)}{\sigma'~\sqrt{2}}\right]$$

Ce type de calcul d’erreur permet de trouver le taux d’erreur sur les éléments binaires.