1. Introduction
Le signal, support de l’information, est devenu le moyen de communication des hommes, entre eux et avec leur environnement. L’objectif premier de ce chapitre et de faire apparaître la distinction entre signaux déterministes (ou certains) et signaux aléatoires, puis, dans un deuxième temps, leur classement en signaux à temps continu et signaux à temps discret.
Un signal est la représentation physique de l’information à transmettre d’une source à son destinataire. Il rend la communication techniquement possible. C’est une grandeur dont l’origine de la nature physique peut être électrique, acoustique, optique, etc.
La théorie du signal est l’étude mathématique de ces signaux, faisant totalement abstraction de leur nature. Un signal sera une fonction du temps \(x(t\)) pouvant représenter une tension \(v(t)\), une intensité \(i(t)\), etc.
Ces signaux sont classés en deux grandes catégories : les signaux déterministes et les signaux aléatoires, eux-mêmes répartis en signaux continus et signaux discrets.
2. Les signaux déterministes
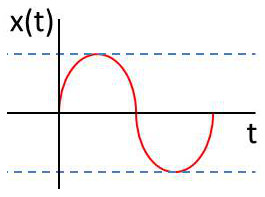Les signaux déterministes sont qualifiés de certains, c’est-à-dire prévisibles dans le temps. Leur évolution en fonction du temps peut être exprimée par un modèle mathématique classique.
Le premier exemple est naturellement celui bien connu de la sinusoïde du courant alternatif :
\[\begin{aligned} x(t)&=A_m~\sin(2~\pi~f_0~t)\\ T_0&=\frac{1}{f_0} \qquad \text{ période de la sinusoïde}\end{aligned}\]
3. Les signaux aléatoires
Il existe des signaux imprévisibles, des fluctuations continues ou des apparitions sporadiques. On les qualifie de signaux aléatoires. Dans un système électronique, le signal aléatoire est un perturbateur (signal nuisible) : on parle alors souvent de bruit de fond. Dans certaines circonstances, le signal de parole peut être considéré comme un signal aléatoire porteur de l’information (signal utile).
Ces signaux sont décrits à partir d’observations statistiques et étudiés en introduisant le calcul des probabilités.
4. Signaux continus et signaux discrets
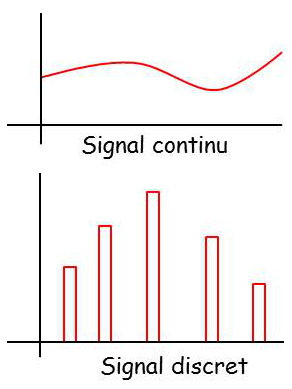Dans un signal continu, l’amplitude et le temps sont des variables continues, c’est-à-dire sans points de discontinuité.
Inversement, dans un signal discret, l’amplitude et le temps sont des variables discontinues. Le signal n’existe (amplitude visible) qu’en des instants bien déterminés et convenus à l’avance.
5. Quelques exemples de signaux discrets
5.1. La fonction porte
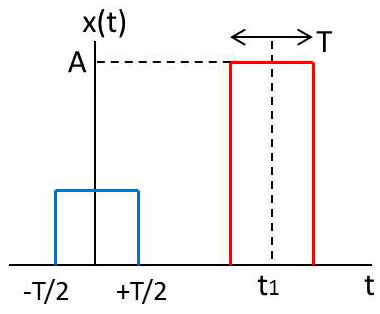Porte d’ouverture \(T\) (en bleu) à centrée à l’origine :
\[\begin{aligned} \Pi_T(t)&=1 \qquad -\tau/2\leqslant t\leqslant \tau/2\\ \Pi_T(t)&=0 \qquad\qquad \text{ailleurs}\end{aligned}\]
Porte d’ouverture \(T'\) centrée en \(t_1\) et d’amplitude \(A\) (courbe rouge) : \[A.\Pi_T'(t-t_1)\]
5.2. La fonction échelon unité (ou Heaviside)
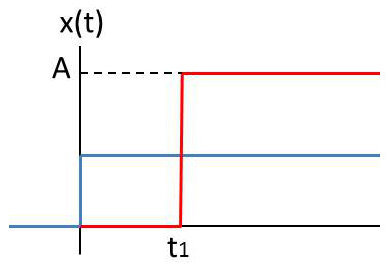Échelon à l’origine :
\[\begin{aligned} u(t)&=1 \qquad t>0\\ u(t)&=0 \qquad t<0\end{aligned}\]
Échelon décalé :
\[\begin{aligned} A~u(t-t_1)=A \qquad t>t_1\\ A~u(t-t_1)=A \qquad t<t_1\end{aligned}\]
5.3. La fonction impulsion de Dirac
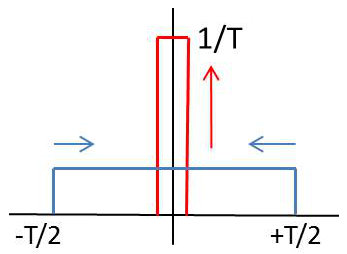Une manière de décrire cette fonction consiste à la considérer comme la limite du rapport d’une fonction porte à son ouverture quand cette dernière tend vers 0. Autrement dit : \[\delta(t)=lim_{T\rightarrow 0}\left\lbrace\frac{1}{T}~~\Pi_T(t)\right\rbrace\]
Une image téméraire serait celle de la surface qui se conserve en prenant de la hauteur alors que la base est étranglée. Dans cette image, la valeur 0 du temps est soigneusement écartée. Ce qui fait d’ailleurs le charme de la théorie des distributions.
Moyennant cette approximation téméraire, on peut dire que, à la limite, son aire correspondante est l’unité : \[\int \limits_{-\infty}^{+\infty}{\delta(t)~dt}=1\]
Pour une impulsion centrée en \(t_1\), donc décalée de \(t_1\) : \[\int \limits_{-\infty}^{+\infty}{\delta(t-t_1)~dt}=1\]
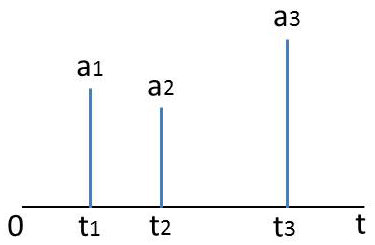Pour caractériser un train d’impulsions on écrira : \[x(t)=\sum_{i}a_i~\delta(t-t_i)\]
Un signal classique est celui d’un train d’impulsions (représentées en rouge) accompagnant une courbe donnée (représentée en bleu).
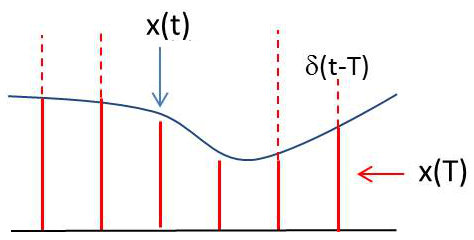Il s’agit de ce que l’on appelle l’échantillonnage de cette fonction ou encore la modulation du train d’impulsions par la fonction continue représentée.
