1. Introduction

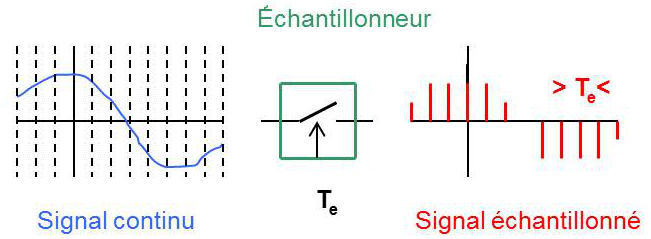De façon idéale, échantillonner un signal continu à temps continu consiste à générer un nouveau signal \(\widetilde{x}(t)\) toujours à temps continu, formé d’une succession des valeurs prises par \(x(t)\) en des instants particuliers, dits instants d’échantillonnage (en général espacés d’un temps constant \(T_e\) appelé période d’échantillonnage) et nul en dehors de ces instants d’échantillonnage.

L’inverse de la période d’échantillonnage \(f_e=1/T_e\) est alors appelé fréquence d’échantillonnage.

D’une façon très schématique, le dispositif d’échantillonnage peut être considéré comme un contact se fermant périodiquement (périodicité \(T_e\)) pendant un temps infiniment bref. Cette opération n’offre d’intérêt que si elle est réversible, c’est-à-dire que si, disposant du signal échantillonné, il est possible de reconstituer le signal d’origine sans perte d’information. L’objectif de ce chapitre est de donner une modélisation mathématique de cette opération, tant dans le domaine temporel que dans le domaine fréquentiel et d’en déduire les conditions que doivent respecter le signal et la fréquence d’échantillonnage pour que cette opération soit réversible.

Pour cela, nous considèrerons dans un premier temps l’échantillonnage comme idéal (durée de chaque échantillon supposée infiniment brève), puis nous étudierons les cas plus pratiques où chaque échantillon a une durée \(\Theta\) non négligeable, et enfin nous terminerons sur le cas très particulier des signaux à bande étroite.

2. Échantillonnage : étude théorique

En choisissant des instants multiples de la période d’échantillonnage \(t_k=k~T_e\) et en utilisant les propriétés des distributions, on peut écrire : \[\widetilde{x}(t)=\sum_{k=-\infty}^{k=+\infty}x(t_k)~\delta(t-t_k)=\sum_{k=-\infty}^{k=+\infty}x(t_k)~\delta(t-k~T_e)\]

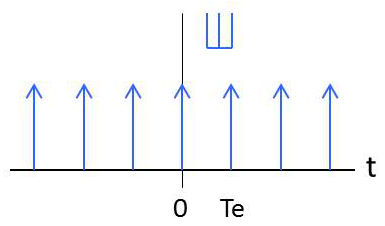
Ce qui peut s’exprimer plus simplement par : \[\widetilde{x}(t)=\sum_{k=-\infty}^{k=+\infty}x(t)~\delta(t-k~T_e)=x(t).\sum_{k=-\infty}^{k=+\infty}\delta(t-k~T_e)=x(t)~\text{Ш}\]

L’expression : \[\text{Ш} =\sum_{k=-\infty}^{k=+\infty}\delta(t-k~T_e)\] symbolise un train d’impulsions régulier de Dirac. On la désigne sous le nom de peigne de Dirac, symbolisé par la lettre cyrillique sha Ш.

Un calcul montre que la transformée de Fourier d’un peigne de Dirac dans l’espace temps est encore un peigne de Dirac dans l’espace des fréquences à un facteur multiplicatif près \(fe=1/Te\).

\[\text{Ш}_e(t) \quad \rightarrow \quad \frac{1}{T_e}\text{Ш}_{T_e}(t)]\]

En désignant par \(\widetilde{X}(f)\) la transformée de Fourier de \(\widetilde{x}(t)\), il vient (théorème de Plancherel) : \[\widetilde{X}(f)=\frac{1}{T_e}X(f)\star\sum_{-\infty}^{+\infty}\delta(f-kf_e)\]

Ce qui peut encore s’écrire :

\[\begin{aligned} \widetilde{X}(f)&=\frac{1}{T_e}\sum_{-\infty}^{+\infty}X(f)\star\delta(f-kf_e)\\ \widetilde{X}(f) &=\frac{1}{T_e}\sum_{k=-\infty}^{+\infty}X(f-kf_e)\end{aligned}\]

2.1. Théorème de Shannon

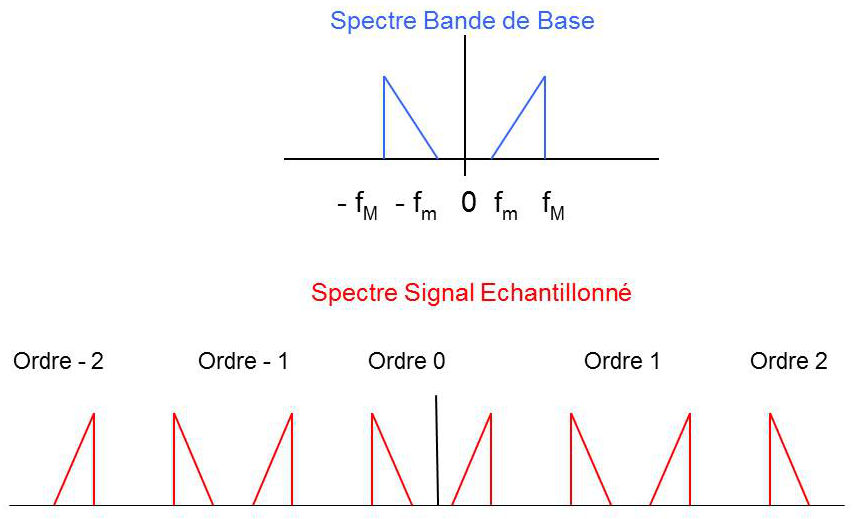
On constate que le spectre du signal échantillonné \(\widetilde{X}(f)\) contient, à un facteur multiplicatif près, le spectre du signal initial (ordre 0). De par la dualité temps - fréquence dans la transformation de Fourier, il est possible de reconstituer le signal d’origine en ne retenant par filtrage passe–bas que l’ordre 0 de la périodisation.

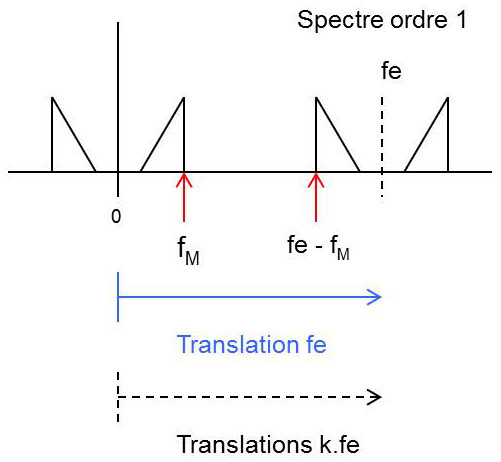Cependant la figure montre que cela n’est possible qu’à une double condition :
— le support du spectre du signal initial est borné ; il existe donc une fréquence maximale \(f_M\) ;
— il est possible de placer la bande de transition du filtre passe–bas de reconstitution entre les fréquences \(f_M\) et \(f_e-f_M\).

Donc, pour éviter toute interférence entre les ordres 0 et 1, il faut \(f_e-f_M>f_M\).

En définitive, la condition de reconstruction revient à \[f_e>2f_M\] qui est la condition ou critère de Shannon.

3. Échantillonnage : étude pratique

En théorie, on admet que \(\theta\) est très petit, mais, dans la pratique, il faut tenir compte de ce temps de fermeture de la porte. Nous considérons deux types d’échantillonneur : l’échantillonneur suiveur et l’échantillonneur bloqueur.

3.1. Échantillonneur suiveur

Avec un échantillonneur suiveur, l’amplitude de chaque échantillon suit la valeur du signal pendant toute sa durée \(\theta\).

On peut modéliser le signal échantillonné :

\[\begin{aligned} \widetilde{x}(t)&=x(t)\sum_{-\infty}^{+\infty}\Pi_{\theta}(t-k~T_e)\\ \widetilde{x}(t)&=x(t)\sum_{-\infty}^{+\infty}\Pi_{\theta}(t)\star\delta(t-k~T_e)\end{aligned}\]

Prenons ensuite la transformée de Fourier de cette dernière relation : \[\widetilde{X}(f)=X(f)\star\left\{\theta\sin c(\pi f_{}\theta)\frac{1}{T_e}\sum_{-\infty}^{+\infty}\delta(f-kf_e) \right\}\] \[\widetilde{X}(f)=X(f)\star\left\{\frac{1}{T_e}\sum_{-\infty}^{+\infty}\theta\sin c(\pi f\theta)~\delta(f-kf_e) \right\}\] \[\widetilde{X}(f)=X(f)\left\{\frac{1}{T_e}\sum_{-\infty}^{+\infty}\theta\sin c(\pi kf_e\theta)\star\delta(f-kf_e) \right\}\] \[\widetilde{X}(f)=\frac{\theta}{T_e}\sum_{-\infty}^{+\infty}\sin c(\pi kf_e\theta)~X(f)\star\delta(f-kf_e)\]

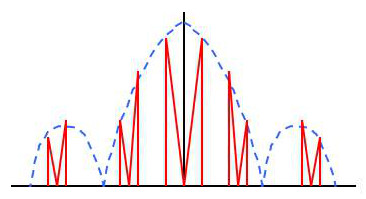Le nom de suiveur est parfaitement justifié. Le spectre est enveloppé par la courbe en sinus cardinal. Cette courbe fixe les amplitudes du spectre aux points de fréquences considérées.

Et en définitive : \[\widetilde{X}(f)=\frac{\theta}{T_e} \sum_{-\infty}^{+\infty}\big[sin c(\pi kf_e\theta)]~X(f-kf_e)\]

3.2. Echantillonneur bloqueur

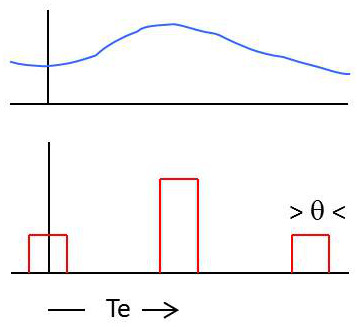Avec un échantillonneur bloqueur, l’amplitude de chaque échantillon est maintenue constante pendant toute sa durée \(\theta\).

On peut alors modéliser le signal de la manière suivante : \[\widetilde{x}(t)=\sum_{k=-\infty}^{k=+\infty}\Pi_{\theta}(t-kT_e~)~x(kT_e-\theta/2)\] \[\widetilde{x}(t)=\sum_{k=-\infty}^{k=+\infty}\Pi_{\theta}(t)\star \delta(t-kT_e)~x(kT_e-\theta/2)\] \[\widetilde{x}(t)=\Pi_{\theta}(t)\star\sum_{k=-\infty}^{k=+\infty} \delta(t-kT_e)~x(t-\theta/2)\] \[\widetilde{x}(t)=\Pi_{\theta}(t)\star\big[ x(t-\theta/2)\sum_{k=-\infty}^{k=+\infty} \delta(t-kT_e)\big]\]

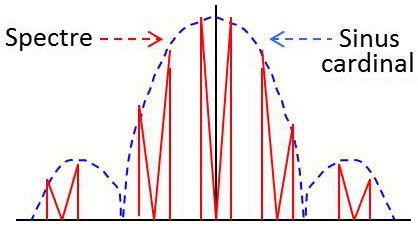Et en prenant la transformée de Fourier de cette dernière relation : \[\widetilde{X}(f)=\theta\sin c(\pi f\theta)~X(f)~e^{-j2\pi f\theta/2}\star\frac{1}{T_e}\sum_{k=-\infty}^{k=+\infty}\delta(f-kf_e)\]

On retrouve toujours le fait que le spectre du signal échantillonné est le périodisé du spectre du signal de départ avec une période \(f_e\), mais cette fois l’ensemble du spectre est affecté d’un coefficient multiplicatif fonction de la fréquence \(\frac{\theta}{T_e}\sin c(\pi f\theta)\) .

La forme de chaque ordre est donc modifiée par rapport au signal d’origine et ce type de signal introduit donc une distorsion lors de la reconstitution du signal, distorsion d’autant plus faible que \(\theta\) est petit.

4. Échantillonnage des signaux à bande étroite

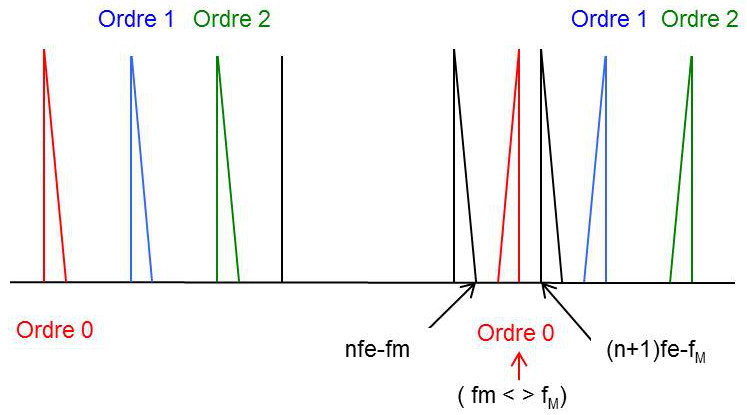Le cas des signaux à bande étroite est particulier comme le montre le spectre, car les ordres peuvent se croiser (sous réserve de certaines valeurs) sans qu’il y ait de chevauchement. Il est bien sûr indispensable d’échantillonner ce signal à une fréquence \(f_e<2f_M\).

L’ordre 0 occupe la bande : \[[-f_M,-f_m]\cup[f_m,f_M]\]

L’ordre 1 occupe la bande : \[[f_e-f_M,f_e-f_m]\cup[f_e+f_m,f_e+f_M]\]

L’ordre \(k\) occupe la bande : \[[kf_e-f_M,kf_e-f_m]\cup[kf_e+f_m,kf_e+f_M]\]

Pour que le chevauchement soit évité, il faut et il suffit qu’il existe un entier \(n\) tel que l’ordre 0 s’insère strictement entre les ordres \(n\) et \(n+1\). De façon plus précise, il faut et il suffit qu’il existe un entier \(n\) tel que : \[\left\{ \begin{array}{r c l} nf_e-f_m &<& f_m\\ (n+1)f_e-f_M &>& f_M \end{array} \right.\]

C’est-à-dire : \[\frac{2f_M}{n+1}<f_e<\frac{2f_m}{n}\]

En définitive, il sera possible d’échantillonner un signal à bande étroite \( [-f_M-f_m]\cup[f_m,f_M] \) à une fréquence d’échantillonnage \(f_e < 2f_M\) si et seulement si : \[n<\frac{f_m}{f_M-f_m}\]

S’il est possible de trouver une ou plusieurs valeurs de \(n\) répondant à cette condition, à chaque valeur de \(n\) correspondra un intervalle de fréquences fourni par la relation précédente à l’intérieur duquel on pourra choisir la fréquence d’échantillonnage.

Prenons par exemple la bande : \([f_m=8kHz~;~f_M=10kHz]\) \[\frac{f_m}{f_M-f_m}=4 \quad \Rightarrow \quad n=0,~1,~2\text{ ou }3\]

Il y a donc 4 possibilités :

\[\begin{aligned} n=o~:&& \frac{2f_M}{n+1}=20~kHz&<f_e<\frac{2f_m}{n}=+\infty &&f_e>20~kHz\\ n=1~:&& \frac{2f_M}{n+1}=10~kHz&<f_e<\frac{2f_m}{n}=16~kHz &&f_e\in[10~kHz~;~16~kHz]\\ n=2~:&& \frac{2f_M}{n+1}=6,6~kHz&<f_e<\frac{2f_m}{n}=8~kHz &&f_e\in[6.6~kHz~;~8~kHz]\\ n=3~:&& \frac{2f_M}{n+1}=5~kHz&<f_e<\frac{2f_m}{n}=5.3~kHz &&f_e\in[5~kHz~;~5.3~kHz]\end{aligned}\]

On remarque que la fréquence d’échantillonnage peut être choisie dans une bande de fréquences d’autant plus basse que \(n\) est grand.