1. Amplificateur BF élémentaire
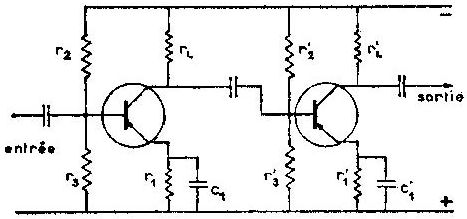 La figure ci-contre représente un amplificateur BF à deux étages à transistors, capacités et résistances. Ce schéma ne diffère de celui que l’on obtiendrait à partir de deux étages à triodes que par l’adjonction de deux résistances \(r_2\) et \(r'_2\).
La figure ci-contre représente un amplificateur BF à deux étages à transistors, capacités et résistances. Ce schéma ne diffère de celui que l’on obtiendrait à partir de deux étages à triodes que par l’adjonction de deux résistances \(r_2\) et \(r'_2\).
Elles servent à stabiliser le gain contre les variations de température et en même temps le tendent moins sensible au remplacement d’un transistor par un autre de caractéristiques légèrement différentes.
Les amplificateurs à liaison directes ont bien plus aisés à réaliser avec des transistors qu’avec des tubes électroniques, en raison des faibles valeurs des tensions d’alimentation nécessaires.
Par suite, on supprime souvent les batteries compensatrices employées dans les montages à tubes. Avec les transistors, comme avec les tubes, on diminue beaucoup la dérive en réalisant des montages symétriques.
2. Montages à symétrie complémentaire
L’existence des transistors des deux types NPN et PNP où courants et batteries sont de sens inverses permet des montages très intéressants par leurs propriétés et en particulier leur simplicité et leur petit volume qui n’ont pas d’équivalent avec les tubes électroniques.
 Parmi ces montages à symétrie complémentaire, il faut citer les circuits logiques, des amplificateurs à liaison directe, des amplificateurs push-pull.
Parmi ces montages à symétrie complémentaire, il faut citer les circuits logiques, des amplificateurs à liaison directe, des amplificateurs push-pull.
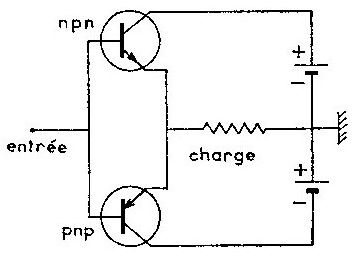
Dans l’étage push-pull sans transformateur de sortie ci-contre, il suffit d’une seule tension d’entrée et non de deux tensions en opposition de phase comme avec les tubes électroniques.
Le transistor PNP fonctionne pendant les alternances négatives du signal d’entrée, le transistor NPN pendant les alternances positives. Ce qui réalise le fonctionnement en classe B qui a l’avantage de prolonger la vie des batteries.
3. Amplificateur opérationnel
Un amplificateur opérationnel, réalisé au moyen d’un ensemble intégré de transistors est très complexe à étudier. Aussi se borne-t-on le plus souvent au relevé expérimental de ses performances.
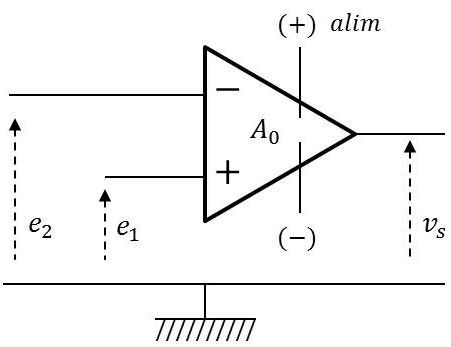 Symbolisé par un triangle, l’amplificateur opérationnel possède deux entrées, \((+)\) et \((-)\). Quand un signal positif est appliqué à l’entrée \((+)\) alors que l’autre entrée est à la masse, le signal de sortie est en phase tandis que celui-ci est en opposition de phase si le signal d’entrée est appliqué à l’entrée \((-)\).
Symbolisé par un triangle, l’amplificateur opérationnel possède deux entrées, \((+)\) et \((-)\). Quand un signal positif est appliqué à l’entrée \((+)\) alors que l’autre entrée est à la masse, le signal de sortie est en phase tandis que celui-ci est en opposition de phase si le signal d’entrée est appliqué à l’entrée \((-)\).
Si deux signaux \((e_1)\) et \((e_2)\) sont appliqués simultanément aux deux entrées, la tension de sortie est proportionnelle à la différence entre ces signaux : \[v=A_0~(e_1-e_2)\]
\(A_0\) est un nombre positif très élevé que l’on appelle gain en chaîne ouverte. Une valeur classique est \(A_0\approx 10^5\).
En définitive, les caractéristiques sont très proches de celles de l’amplificateur idéal, à savoir :
-
Gain \(A_0=\infty\)
-
Résistance d’entrée \(R_e=\infty\)
-
Résistance de sortie \(R_s=0\)
-
Bande passante \(B=\infty\)
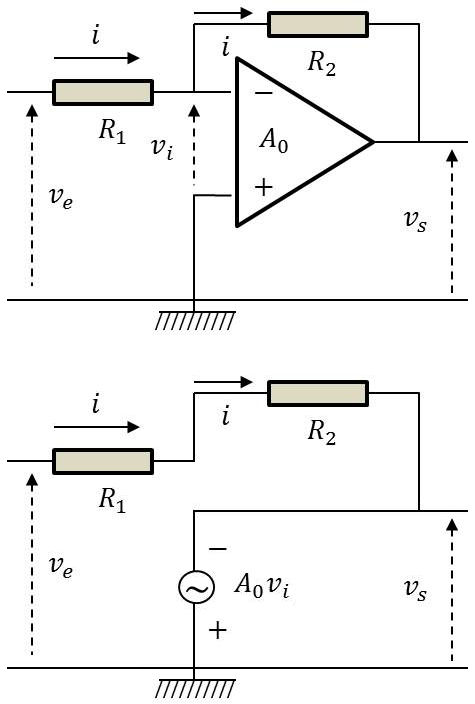 Le montage classique de l’amplificateur opérationnel consiste à insérer deux résistances \(R_1\) et \(R_2\) (ou plus généralement deux impédances \(Z_1\) et \(Z_2\)) respectivement en série à l’entrée négative et en parallèle entre cette entrée et la sortie, la borne positive étant reliée directement à la masse.
Le montage classique de l’amplificateur opérationnel consiste à insérer deux résistances \(R_1\) et \(R_2\) (ou plus généralement deux impédances \(Z_1\) et \(Z_2\)) respectivement en série à l’entrée négative et en parallèle entre cette entrée et la sortie, la borne positive étant reliée directement à la masse.
Comme la résistance d’entrée en chaîne ouverte est infinie (donc \(R_e=\infty\)), c’est la même intensité \(i\) qui traverse ces résistances.
Si l’on effectue le calcul, la résistance d’entrée en chaîne fermée, c’est-à-dire (\(R_e=v_1/i\)), il vient : \[v_1~(1+A_0)=R_2~i\quad\Rightarrow\quad R'_e=\frac{R_2}{1+A_0}\approx 0\]
Dans ces conditions, la résistance d’entrée, qui était infinie en chaîne ouverte, devient nulle en chaîne fermée.
On dit que cet amplificateur possède entre ses bornes une masse virtuelle. Le mot virtuel est utilisé pour bien montrer que, si la tension est nulle (\(v_1=0\)), le court-circuit n’est cependant traversé par aucun courant.
On obtient alors (calcul élémentaire) : \[A=\frac{v_s}{v_e}=-\frac{R_2}{R_1}\]
Et de manière plus générale (en notation complexe) : \[A=\frac{V_s}{V_e}=-\frac{Z_2}{Z_1}\]
Cet amplificateur est appelé opérationnel, car, en régime quelconque, le quotient des deux impédances (fonctions de \(p\)) est une fonction de \(p\), variable de Laplace.
4. Amplificateur pratique
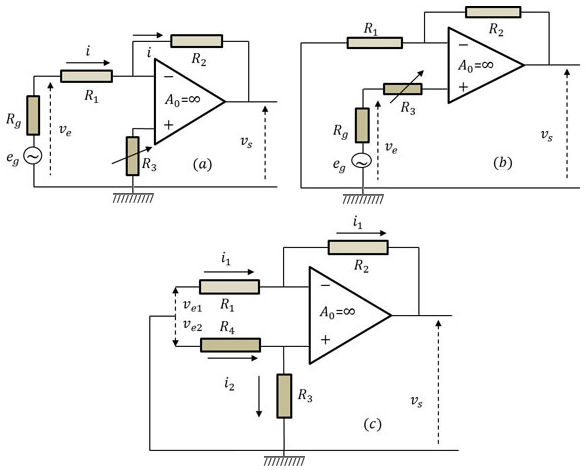 Les trois modes d’utilisation sont respectivement (voir figure) l’amplificateur inverseur, l’amplificateur non inverseur et l’amplificateur différentiel.
Les trois modes d’utilisation sont respectivement (voir figure) l’amplificateur inverseur, l’amplificateur non inverseur et l’amplificateur différentiel.
a) Amplificateur inverseur
La borne positive est reliée à la masse par l’intermédiaire de \(R_3\). Cette résistance, utile du point de vue électronique (limitation des dérives), n’est traversée par aucun courant et n’a aucune influence sur le gain de l’amplificateur. Un calcul facile montre que : \[A=\frac{v_s}{v_e}=-\frac{R_2}{R_1}\]
b) Amplificateur non inverseur
La résistance d’entrée étant très grande, le générateur d’attaque ne débite pratiquement pas et l’on a pratiquement : \[v_e~\approx~e_g\]
D’autre part, les bornes (2) et (3) étant sensiblement au même potentiel, on a : \[v_e=v_3=v_2\]
Et après un calcul élémentaire : \[A=\frac{v_s}{v_e}=\frac{R_1+R_2}{R_1}\]
On pourra remarquer que : \[R_2\gg R_1\quad\Rightarrow\quad A~\approx~\frac{R_2}{R_1}\]
c) Amplificateur différentiel
Si l’on suppose l’amplificateur idéal (\(A_0=\infty\) et \(R_e=\infty\)), c’est le même courant \(i_1\) qui circule dans les branches \(R_1\) et \(R_2\), tandis que c’est le même courant \(i_2\) qui traverse les branches \(R_3\) et \(R_4\). En application du principe de superposition, on peut écrire : \[v_s=-\frac{R_2}{R_1}~v_{e1}+\frac{R_1+R_2}{R_1}~\frac{R_3}{R_3+R_4}~v_{e2}\]
Et dans l’hypothèse : \[R_1=R_4\quad;\quad R_2=R_3\]
Il vient : \[A=\frac{v_s}{v_{e2}-v_{e1}}=\frac{R_2}{R_1}\]
5. Amplificateur opérationnel : techniques analogiques
Nous ne traiterons ici que des opérations analogiques simples telles que l’addition, la dérivation et l’intégration (duale de la première).
5.1. Addition
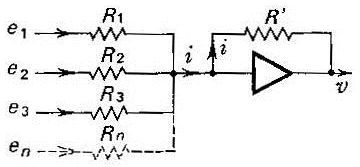 Les différentes tensions d’entrée (\(e_1\), \(e_2\), etc.) sont appliquées entre l’entrée de l’amplificateur et la masse qui n’est pas représentée.
Les différentes tensions d’entrée (\(e_1\), \(e_2\), etc.) sont appliquées entre l’entrée de l’amplificateur et la masse qui n’est pas représentée.
En raison de la masse virtuelle (\(v_1=0\)), il vient : \[i=\frac{e_1}{R_1}+\frac{e_2}{R_2}+\dots+\frac{e_n}{R_n}\]
Par suite : \[v=-R'i=-\frac{R'}{R_1}~e_1-\frac{R'}{R_2}-\dots-\frac{R'}{R_n}~e_n\]
Si on fait : \[R_1=R_2=\dots= R_n\]
Il vient : \[v=-\frac{R'}{R_1}~(e_1+e_2+\dots+e_n)\]
Cependant, si l’on se donne des valeurs convenables pour \(R_1,~R_2,~\dots,~R_n\), chacune des grandeurs d’entrée est, avant l’addition aux autres grandeurs, multipliée par une constante.
5.2. Intégration
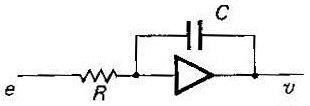 Pour obtenir l’intégration d’un signal d’entrée, il suffit de remplacer la résistance \(R_2\) par une capacité \(C\).
Pour obtenir l’intégration d’un signal d’entrée, il suffit de remplacer la résistance \(R_2\) par une capacité \(C\).
On a (équations des branches) :
\[\begin{aligned} e&=R~i\quad;\quad v=-\frac{1}{C}\int_0^t i~dt\\ i~v&=-\frac{1}{R~C}\int_0^t e~dt\end{aligned}\]
Soit, en écriture opérationnelle : \[\frac{v}{e}=-\frac{1}{R~C~p}\]
Si la constante de temps est choisie telle que : \[\tau=R~C=1\]
En choisissant par exemple \(R=1~{\rm M}\Omega\) , \(C=1~\mu\rm F\), on obtient alors exactement la valeur (\(-1/p\)) (symbole de l’opérateur intégral).
Remarque
On aurait pu obtenir plus directement ces résultats en écrivant que : \[\frac{v}{e}=-\frac{Z_2}{Z_1}=-\frac{1/C~p}{R}=-\frac{1}{R~C~p}\]
5.3. Dérivation
Pour obtenir la dérivation, il suffit de permuter la résistance et la capacité : \[\frac{v}{e}=-\frac{R}{1/C~p}=-R~C~p\]

