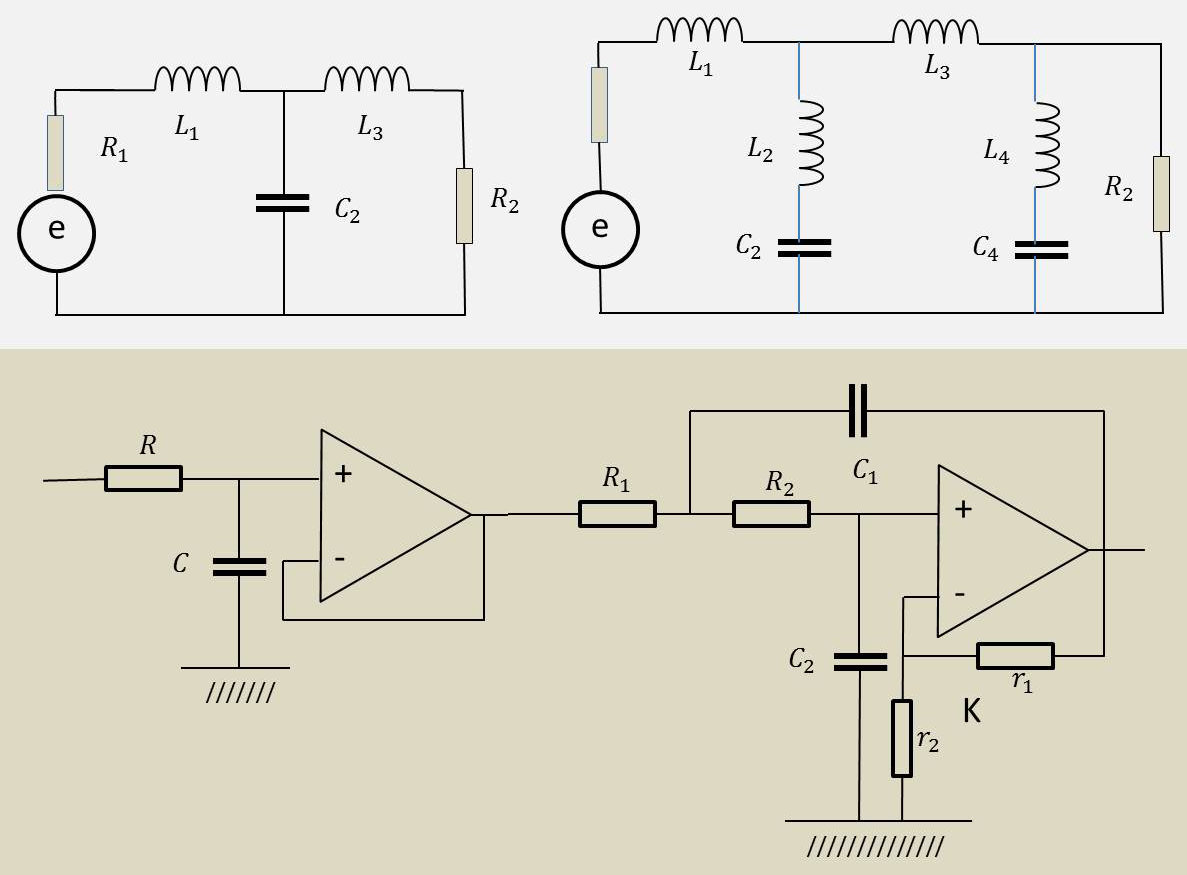
Deux filtres passifs passe-bas, à inductances et capacités, de types polynomial (1) et elliptique (2). Un troisième filtre actif passe-bas, à résistances, capacités et amplificateurs, de type polynomial (3).
Après la théorie du signal, voici des aspects du réel : structures de base et composants disponibles, vers la pré-industrialisation.
Le filtre passif puise toute son énergie dans la source e avec une certaine dégradation, les composants présentant des pertes généralement faibles. On définit alors deux énergies, transmise et réfléchie par ce quadripôle particulier. Une adaptation d'impédance est nécessaire.
Au contraire, le filtre actif puise son énergie (perdue par effet Joule) dans les alimentations régulées des amplificateurs. Sa caractéristique : une impédance d'entrée pratiquement infinie et une impédance de sortie pratiquement nulle.
Deux technologies bien distinctes, mais appelées à satisfaire une même contrainte : réaliser une fonction de transfert sur une gamme de fréquences (rapport des tensions entrée / sortie).
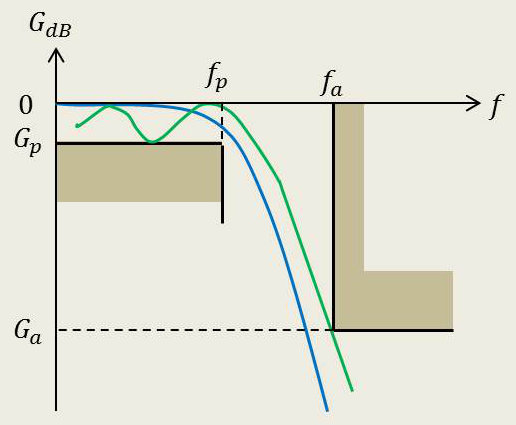
Dans les faits, un gabarit de gain \(G_{dB}(f)\) est imposé. Au concepteur de trouver l'approximation mathématique qui génèrera une fonction de transfert dont le logarithme du module s'inscrira au mieux dans ce gabarit (plusieurs solutions).
Notre étude est en trois parties :
La première, introduction à chacune des deux autres, ou problème de l'approximation, consiste à trouver l'expression d'une fonction de transfert (complexe) inscriptible dans le gabarit imposé. La deuxième (ou la troisième) consiste à déterminer une structure, puis calculer les valeurs des composants à partir de la fonction de transfert (directement ou indirectement).
L'ensemble de l'opération est la synthèse du filtre. Fonction de la variable complexe, techniques d'approximations et analyse numérique impliquant l'ordinateur, électronique et réseaux linéaire : nous sommes au cœur de la théorie des circuits.
Conférences données à l'INSA Rennes (1976), l'UBO Brest (1978 - 80) et l'ENSTA Paris (années 1980).
