1. Facteur de bruit
1.1. Définition
Le facteur de bruit d’un quadripôle (de gain \(G\)) représente la dégradation du rapport signal sur bruit à la traversée de ce quadripôle. Le facteur de bruit est défini par : \[F=\frac{(S/P_b)_E}{(S/P_b)_S}=\frac{1}{G}\cdot\frac{P_{bS}}{P_{bE}}\]
L’expérience prouve que la puissance de bruit en sortie \(P_{bS}\) est supérieure à \(G.P_{bE}\), donc que \(F>1\).
\(T_0\) étant la température absolue en \(E\), et \(\Delta f\) la bande passante de l’amplificateur (ou quadripole), on a : \[P_{bE}=k~T_0~\Delta f\]
On peut donc écrire : \[P_{bS}=F~G~k~T_0~\Delta f=G~k~T_0~\Delta f+P_{sup}\]
Cette puissance supplémentaire \(P_{sup}\) est attribuable à la traversée de \(Q\). On a alors, en introduisant la température de bruit \(T_e\) du quadripole : \[P_{bS}=k~T_0~G~\Delta f+k~T_e~G~\Delta f= k~(T_0+T_e)~G~\Delta f\]
Par comparaison, on voit donc que : \[T_0+T_e=F~T_0\] \[F=1+\frac{T_e}{T_0}\]
1.2. Température équivalente de bruit
On peut définir à présent la température équivalente de bruit du quadripôle \(Q\) par la relation : \[T_e~=~(F-1)~T_0\]
Elle exprime le bruit propre sous forme d’une élévation de température de la source de bruit de résistance interne \(R_g\).
Tout se passe comme si le quadripôle n’était pas bruyant, mais que la source était par contre portée à la température \(T_0+T_e\).
Un facteur de bruit d’une valeur de l’ordre de 7 dB à 8 dB est convenable, il paraît difficile de descendre au-dessous de 3,5 dB.
1.3. Facteur de bruit moyen
Considérant une bande de fréquences \(\Delta f=f_2-f_1\), on peut définir un facteur de bruit moyen \(\overline{F}\) par l’expression : \[\overline{F}=\frac{\int_{f_1}^{f_2}F(f)~G(f)~df}{\int_{f_1}^{f_2}G(f)~df}\]
En général, pour un amplificateur, \(\overline{F}\) diffère assez peu de \(F(f)\) dans sa bande passante.
2. Composition des facteurs de bruit
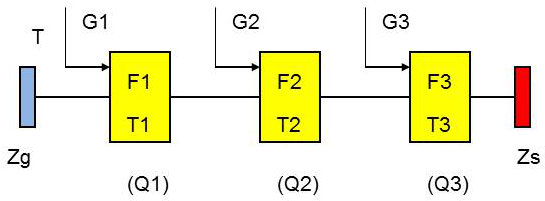On considère trois amplificateurs en série, de gains respectifs \(G1,~G2,~G3\), de températures de bruit respectives \(T1,~T2,~T3\) et de facteurs de bruit respectifs \(F1,~F2,~F3\).
On s’intéresse aux puissances de bruit en sortie de chacun des quadripôles \(Q1,~Q2,~Q3\) :
\[\begin{aligned} &P_{b1}=k~T~G_1~\Delta f+k~T_1~G_1~\Delta f\\ &P_{b2}=k~T~G_1~G_2~\Delta f+k~T_1~G_1~G_2~\Delta f+k~T_2~G_2~\Delta f\\ &P_{b3}=k~T~G_1~G_2~G_3~\Delta f+k~T_1~G_1~G_2~G_3~\Delta f+k~T_2~G_2~G_3~\Delta f+k~T_3~G_3~\Delta f\end{aligned}\]
Par suite : \[P_{b3}=k~G_1~G_2~G_3~\Delta f\left\{T+T_1+\frac{T_2}{G_2}+\frac{T_3}{G_1~G_2}\right\}\]
La température de bruit de la chaîne est donc : \[T_B=T_1+\frac{T_2}{G_1}+\frac{T_3}{G_1~G_2}\]
Sachant que : \[F=1+\frac{T_b}{T}\]
On a :
\[\begin{aligned} &T+T_b~=~FT~=~T+T_1+\frac{T_2}{G_1}+\frac{T_3}{G_1~G_2}\\ &\frac{T_1}{T}~=~F_2-1 \quad ;\quad\frac{T_2}{T}~=~F_3-1\end{aligned}\]
De sorte que : \[F~=~F_1+\frac{F_2-1}{G_1}+\frac{F_3-1}{G_1~G_2}\]
Le facteur de bruit du deuxième étage est divisé par le gain du premier étage. On a donc intérêt à privilégier le facteur de bruit du premier étage et à accroître son gain.
La relation est connue sous le nom de formule des cascades de quadripôles ou formule de Friss. Elle peut également s’écrire en fonction des températures de bruit grâce à l’équivalence : \[Te~=~T_1+\frac{T_2}{G_1}+\frac{T_3}{G_1~G_2}+ \dots +\frac{T_n}{G_1~G_2~\dots~G_n}\]
\(T_e\) est la température de bruit équivalente du système de quadripôles.
3. Facteur de bruit d’un quadripôle passif
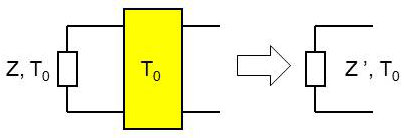Considérons un quadripôle constitué uniquement de composants passifs, placés à la même température \(T_0\). Si une impédance \(Z\), portée à cette même température, est connectée à ses bornes d’entrée, l’ensemble est équivalent à un quadripôle passif d’impédance \(Z'\).
La puissance de bruit disponible en entrée est : \[P_{be}=k~T_0~\Delta f\]
La puissance de bruit disponible en sortie est aussi : \[P_{bs}=k~T_0~\Delta f\]
Mais on a également : \[P_{bs}=F~G~k~T_0~\Delta f\]
Il s’ensuit que : \[F~G=1 \quad \Rightarrow \quad F=\frac{1}{G}=A\]
Le facteur de bruit d’un quadripôle passif est donc égal à l’inverse de son gain en puissance disponible, c’est-à-dire égal à son atténuation.
4. Cas du quadripôle actif
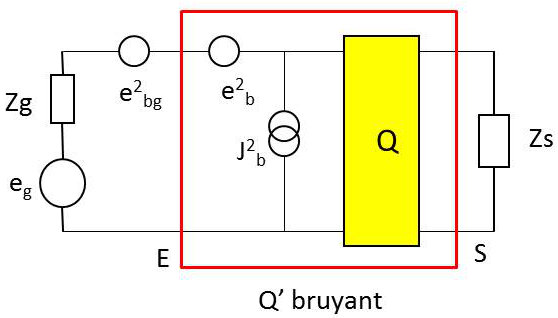Tout quadripôle réel peut être représenté par un quadripôle non bruyant associé à deux sources de bruit \(e^2_b\) et \(j^2_b\). Revenant à la définition, on peut montrer que le facteur de bruit peut s’écrire sous la forme :
\[\begin{aligned} &F~=~A+BR_g+\frac{C}{R_g}\\ &A,~B,~C\text{ : constantes indépendantes de}~ R_g\end{aligned}\]
Lorsque le quadripôle est attaqué par une source de résistance \(R_g\), le facteur de bruit admet un minimum pour une valeur optimale de la résistance d’attaque \(R_g\) : \[R_{g~opt}=\sqrt{\frac{C}{B}}\]
5. Calcul de la température de bruit
Considérons l’exemple d’une liaison spatiale. Le récepteur de température de bruit \(T_R\) est relié à l’antenne de température apparente \(T_A\) par l’intermédiaire d’une ligne d’affaiblissement \(A\) et de température vraie \(T_L\).
On effectue les calculs pour la bande passante de l’ensemble du circuit de réception. La température équivalente de bruit de la chaîne de réception, vue au niveau de l’antenne-source, est égale à (formule de Friss) : \[(A - 1)~T_L~[\text{contribution ligne}] + A~T_R~[\text{contribution récepteur}]\]
D’où une température totale de bruit : \[T_{tot}=T_A+(A-1)~T_L+A~T_R\]
6. Réduction du bruit dans les systèmes de transmission
Pour réduire la puissance de bruit dans un système de transmission, il est nécessaire de diminuer sa température de bruit.
Ainsi, dans l’exemple précédent, on utilise des antennes à faible température apparente (type Cassegrain), une ligne à faible perte éventuellement refroidie et un récepteur à très faible bruit pour lequel on a également recours à des techniques cryogéniques.
Dans le cas de récepteurs ultra-sensibles pour communications par satellites, il faut refroidir les circuits d’entrée (température voisine de 4° K) et avoir recours à des masers comme éléments d’amplification. Dans le cas de réceptions moins critiques, des amplificateurs paramétriques refroidis suffisent (cas de récepteurs radar).
On a également intérêt à réduire au mieux la bande passante du récepteur dans la limite des exigences du signal transmis. Dans un certain nombre de liaisons (radio ou télédiffusion, télémesures, téléphonie, etc.), le signal à transmettre doit être adapté au canal de transmission par des techniques de modulation (amplitude, fréquence). On peut montrer que, pour des conditions identiques de rapport signal sur bruit avant démodulation, une amélioration importante de ce rapport peut être obtenue en FM.
En radiodiffusion sonore, l’amélioration obtenue en FM par rapport à celle obtenue en AM (ou gain de modulation) est d’environ 19 dB au détriment d’une bande passante six fois plus large. Mais, en pratique, cet avantage n’est effectif que si le rapport S/N avant démodulation dépasse un certain seuil (de l’ordre de 6 à 10 dB).
En dessous de ce seuil, la dégradation du rapport S/N après démodulation est spectaculaire et on parle de capture du signal par le bruit. Sinon, l’amélioration du rapport S/N après démodulation est très nette et on parle alors de capture du bruit par le signal.
Une illustration courante de ce phénomène est la recherche de l’accord d’un récepteur FM : le bruit de fond est important en phase de recherche et disparaît totalement lorsque l’accord est réalisé, la capture du bruit par le signal s’effectuant en fait grâce au signal porteur.
