1. Introduction

Pour la sortie du quadripôle, on adopte les conventions du système générateur.

Un quadripôle passif fonctionnant en régime sinusoïdal est caractérisé par quatre grandeurs :

• deux tensions \(U_1,~U_2\) ;

• deux courants \(I_1,~I_2\).

Si deux grandeurs sont fixées, les deux autres sont déterminées. Il est donc possible d’obtenir et de définir différentes matrices selon les variables couplées.

Les équations linéaires du quadripôle : \[\left\{ \begin{aligned} &U_1=Z_{11}~I_1+Z_{12}~I_2\\ &U_2=Z_{21}~I_1+Z_{22}~I_2 \end{aligned} \right.\]

suggèrent l’introduction naturelle de formes matricielles.

1.1. Matrice impédance (Z)

\[\begin{pmatrix} U_1\\ U_2 \end{pmatrix} = \begin{pmatrix} Z_{11}&Z_{12}\\ Z_{21}&Z_{22} \end{pmatrix} \times \begin{pmatrix} I_1\\ I_2 \end{pmatrix}\qquad \text{ou encore :}\quad (U)=(Z)\times (I)\]

Note importante

L’écriture du système d’équation à signes positifs suppose que le calcul ait été fait dans une configuration \(I_2\) sens entrant dans le quadripôle.

Si tel n’est pas le cas, on doit écrire, en vertu du théorème de réciprocité : \[Z_{12}=-Z_{21}\]

1.2. Matrice admittance (Y)

La matrice admittance est le cas dual du précédent. On aura donc successivement,

– pour le système : \[\left\{ \begin{aligned} &I_1=Y_{11}~U_1+Y_{12}~U_2\\ &I_2=Y_{21}~U_1+Y_{22}~U_2 \end{aligned} \right.\]

– pour la matrice associée : \[\begin{pmatrix} I_1\\ I_2 \end{pmatrix} = \begin{pmatrix} Y_{11}&Y_{12}\\ Y_{21}&Y_{22} \end{pmatrix} \times \begin{pmatrix} U_1\\ U_2 \end{pmatrix}\qquad \text{ou encore :}\quad (I)=(Y)\times (U)\]

et, comme précédemment avec l’impédance : \[Y_{12}=-Y_{21}\]

1.3. Matrice transférance (T) ou matrice chaîne

On exprime les deux grandeurs d’entrée en fonction des deux grandeurs de sortie : \[\left\{ \begin{aligned} U_1&=A~U_2+B~I_2\\ I_1&=C~U_2+D~I_2 \end{aligned} \right.\]

Donc, sous la forme matricielle : \[\begin{pmatrix} U_1\\ I_1 \end{pmatrix} = \begin{pmatrix} A&B\\ C&D \end{pmatrix} \times \begin{pmatrix} U_2\\ I_2 \end{pmatrix} \qquad\text{ou encore :}\quad \begin{pmatrix} U_1\\ I_1 \end{pmatrix} = \begin{pmatrix} T \end{pmatrix} \times \begin{pmatrix} U_2\\ I_2 \end{pmatrix}\]

En appliquant le théorème de réciprocité, on démontre que : \[A~D-BC~=1\]

C’est une propriété importante du déterminant de la matrice chaîne.

1.4. Matrices (G) et (H)

Utilisant d’autres combinaisons des grandeurs d’entrée et de sortie, on obtient deux autres types de matrices : \[\begin{pmatrix} I_1\\ U_2 \end{pmatrix} = \begin{pmatrix} G \end{pmatrix} \times \begin{pmatrix} U_1\\ I_2 \end{pmatrix} \qquad\text{ou encore :}\quad \begin{pmatrix} U_1\\ I_2 \end{pmatrix} = \begin{pmatrix} H \end{pmatrix} \times \begin{pmatrix} I_1\\ U_2 \end{pmatrix}\]

2. Association de quadripôles

2.1. Branchement série

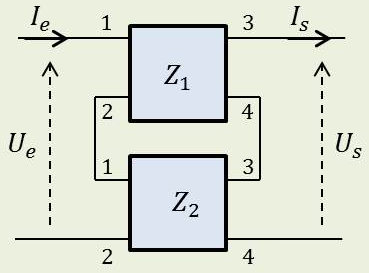Entrées en série et sorties en série.

\[\begin{aligned} &I_e=I_1=I'_1\qquad;\qquad U_e=U_1+U'_1\\ &I_s=I_2=I'_2\qquad;\qquad U_s=U_2+U'_2\end{aligned}\]

Matrice impédance résultante : \[(Z)=(Z_1)+(Z_2)\]

Les matrices impédance de deux quadripôles en série s’ajoutent.

2.2. Branchement parallèle

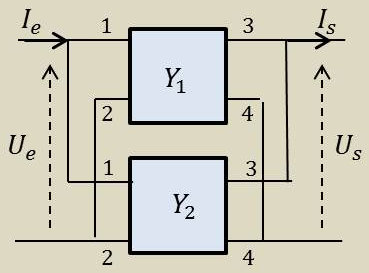Entrées en parallèle et sorties en parallèle.

\[\begin{aligned} &U_e=U_1=U'_1\qquad;\qquad I_e=I_1+I'_1\\ &U_s=U_2=U'_2\qquad;\qquad I_s=I_2+I'_2\end{aligned}\]

Matrice admittance résultante : \[(Y)=(Y_1)+(Y_2)\]

Les matrices admittance de deux quadripôles en parallèle s’ajoutent.

2.3. Branchement mixte parallèle – série

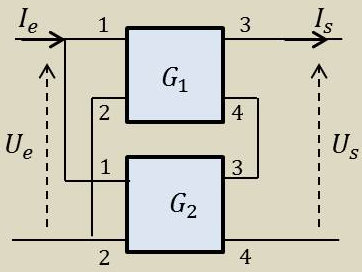Entrées en parallèle et sorties en série.

\[\begin{aligned} &U_e=U_1=U'_1\qquad;\qquad I_e=I_1+I'_1\\ &U_s=U_2=U'_2\qquad;\qquad I_s=I_2+I'_2\end{aligned}\]

Matrice (G) résultante : \[(G)=(G_1)+(G_2)\]

Les matrices en (G) de deux quadripôles en parallèle série s’ajoutent.

2.4. Branchement mixte série – parallèle

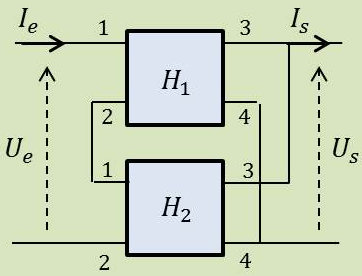Entrées en série et sorties en parallèle.

On en déduit (principe de dualité) : \[(H)=(H_1)+(H_2)\]

Les matrices hybrides de deux quadripôles en série parallèle s’ajoutent.

2.5. Branchement en cascade

Le branchement en cascade est la configuration classique des systèmes de transmission : \[\begin{pmatrix} U_1\\ I_1 \end{pmatrix} = \begin{pmatrix} T_1 \end{pmatrix} \times \begin{pmatrix} U_2\\ I_2 \end{pmatrix} \quad;\quad \begin{pmatrix} U'_1\\ I'_1 \end{pmatrix} = \begin{pmatrix} T_2 \end{pmatrix} \times \begin{pmatrix} U'_2\\ I'_2 \end{pmatrix}\]

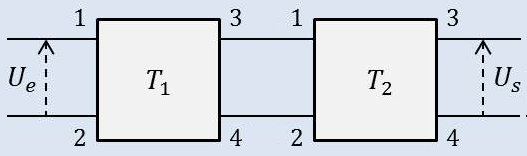Comme on a \(U_2=U'_1\) et \(I_2=I'_1\), il vient : \[(T)=(T_1)\times(T_2)\]

La matrice de transfert équivalente est le produit des matrices de transfert.

3. Matrices fondamentales

Il est toujours possible d’établir directement la matrice d’un quadripôle en appliquant la loi des mailles indépendantes ou la loi des nœuds, mais ce calcul peut s’avérer très lourd. Il est plus simple et plus rapide d’utiliser le calcul matriciel : on décompose le quadripôle en éléments quadripôles simples et on lui applique les lois d’association des quadripôles ; il suffit alors de choisir l’association la plus astucieuse suivant la structure globale qui se présente.

3.1. Deux matrices élémentaires (duales)

Le calcul des deux matrices élémentaires repose essentiellement sur deux structures très simples à une seule impédance : l’impédance série et l’impédance parallèle (dualité).

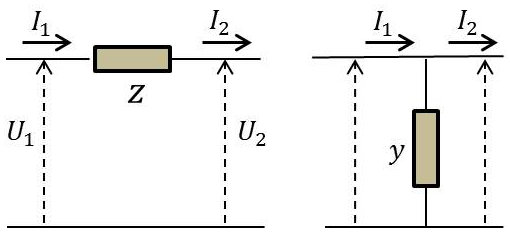– Impédance en série : \[\left\{ \begin{aligned} &U_1=U_2+Z~I_2\\ &I_1=0+I_2 \end{aligned} \right. \quad\Rightarrow\quad (T_s)= \begin{pmatrix} 1&z\\ 0&1 \end{pmatrix}\]

– Impédance en parallèle : \[\left\{ \begin{aligned} &U_1=U_2\\ &I_1=y~U_2+I_2 \end{aligned} \right. \quad\Rightarrow\quad (T_p)= \begin{pmatrix} 1&0\\ y&1 \end{pmatrix}\]

3.2. Matrices déclinées

Pour une matrice à deux éléments dite en L : \[(T_L)=(T_s)\times(T_p)\qquad\text{ou encore :}\quad(T_L)=(T_p)\times(T_s)\]

Pour une matrice à trois éléments dite en T : \[(T_T)=(T_p)\times(T_s)\times(T_p)\]

Pour une matrice à trois éléments dite en \(\Pi\) : \[(T_{pi})=(T_s)\times(T_p)\times(T_s)\]

4. Cascade de quadripôles. Impédance caractéristique

On considère une chaîne de quadripôles dans l’ordre suivant : \[(T)=(T_{(4)})\times(T_{(3)})\times(T_{(2)})\times(T_{(1)})\]

c’est-à-dire à partir de la charge utile vers l’entrée du quadripôle, là où elle est vue (et non pas dans l’ordre direct).

L’impédance caractéristique \(Z_c\) est l’impédance telle que, si elle est branchée à la sortie, l’impédance vue de l’entrée du quadripôle lui soit égale. On doit donc avoir : \[Z_c=\frac{U_2}{I_2}=\frac{U_1}{I_1}\qquad\text{soit}\qquad \frac{U_2}{U_1}=\frac{I_2}{I_1}=\lambda\]

Ou encore : \[\begin{pmatrix} U_2\\ I_2 \end{pmatrix} = \begin{pmatrix} \lambda&0\\ 0&\lambda \end{pmatrix} \times \begin{pmatrix} U_1\\ I_1 \end{pmatrix}\]

\(\lambda\) est donc racine de : \[\begin{vmatrix} T_{11}-\lambda&T_{12}\\ T_{21}&T_{22}-\lambda \end{vmatrix} =0\]

\(\lambda\) apparaît donc comme valeur propre de la matrice chaîne. Elle est donc solution de l’équation caractéristique de la matrice : \[\lambda^2-\lambda~(T_{11}+T_{22})+|T|=0\]

Si nous reprenons le calcul à partir de la définition de l’impédance caractéristique, nous obtenons :

\[\frac{U_1}{I_1}=\frac{T_{11}~U_2+T_{12}~I_2}{T_{21}~U_2+T_{22}~I_2}\qquad\Rightarrow\qquad Z_c=\frac{T_{11}~Z_c+T_{12}}{T_{21}~Z_c+T_{22}}\]

\(Z_c\) est donc solution de l’équation : \[Z_c^2+\frac{T_{22}-T_{11}}{T_{21}}~Z_c-\frac{T_{12}}{T_{21}}=0\]