1. Les différents modes de couplage

Le récepteur radio donne une bonne idée de la question des circuits couplés. L’antenne reçoit des courants de haute fréquence qu’il faut transmettre d’une manière particulière à d’autre circuits. Il s’agit d’un passage d’énergie d’un étage (dit amplificateur) à l’autre, donc d’un couplage.

Parmi les nombreux procédés de couplage, il existe trois types fondamentaux :

• le couplage par résistance (figure 1) ;

• le couplage par capacité (figure 2) ;

• le couplage par inductance (figure 3).

Nous insisterons essentiellement sur ce dernier couplage, appelé encore couplage magnétique, la liaison étant assurée par un véritable transformateur (c’est-à-dire sans noyau de fer doux).

Pour tenir compte des fuites – inévitables – dans les calculs de circuits couplés par inductance, on introduit un coefficient de couplage noté généralement \(M\) entre les deux enroulements, l’un appelé primaire et l’autre appelé secondaire : \[K=\frac{M}{\sqrt{L_1~L_2}}\quad;\quad 0<K<1\]

\(L_1,~L_2\) : coefficients d’auto-induction des enroulements du primaire et du secondaire.

2. Circuits couplés accordés

Pour \(K\approx 1\), on dit que le couplage est serré.

Pour \(K\ll 1\), on dit que le couplage est lâche.

Ce dernier cas est notamment celui du couplage entre deux antennes d’un poste émetteur et d’un poste récepteur, le courant circulant dans l’antenne réceptrice étant sans action (ou sans influence) sur l’antenne émettrice.

Un circuit oscillant série alimenté par une tension alternative de valeur efficace constante, mais de fréquence variable se comporte comme un filtre plus ou moins sélectif, suivant la valeur de son coefficient de qualité.

Cependant, il ne s’agit pas d’un filtre utilisable au sens classique du terme quand faut sélectionner une petite bande de fréquence (cas des amplificateurs à moyenne fréquence).

Pour se rapprocher de la notion de filtre, il faut utiliser alors deux circuits oscillants en les couplant. Ce couplage confère alors à l’ensemble des deux circuits des propriétés nouvelles qui deviennent intéressantes.

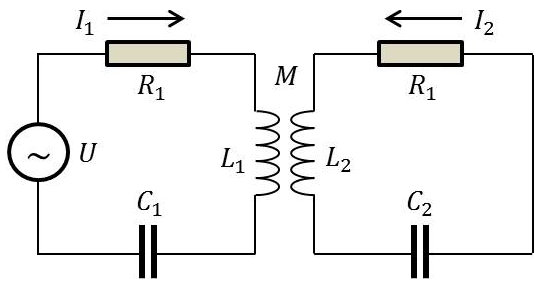
Le premier circuit étant alimenté par une tension alternative de valeur efficace constante et de fréquence variable, déterminons le courant \(I_2\) absorbé par le deuxième circuit.

En régime permanent, le générateur impose sa fréquence aux deux circuits oscillants qui sont ainsi soumis à des oscillations forcées. Le couplage est supposé serré, les équations de fonctionnement (calcul des mailles) sont celles du transformateur : \[\left\{ \begin{aligned} U&=Z_1~I_1+j~M~\omega~I_2\qquad (1)\\ 0&=Z_2~I_2+j~M~\omega~I_1\qquad (2) \end{aligned} \right.\]

Posons : \[\left\{ \begin{aligned} Z_1=R_1+j~X_1\\ Z_2=R_2+j~X_2 \end{aligned} \right. \qquad\qquad\\ \left\{ \begin{aligned} X_1=L_1~\omega-\frac{1}{C_1~\omega}\\ X_2=L_1~\omega-\frac{1}{C_2~\omega} \end{aligned} \right.\]

Il vient alors : \[I_2=\frac{-j~M~\omega~U}{(R_1+j~X_1)~(R_2+j~X_2)+M^2~\omega^2}\]

et pour le module: \[|I_2|=\frac{M~\omega~U}{\sqrt{(R_1~X_2+R_2~X_1)^2+(M^2~\omega^2+R_1~R_2-X_1~X_2)^2}}\]

3. Courbe de réponse

3.1. Expression de l’intensité

On suppose que les pulsations propres des deux circuits résonants sont très voisines : \[\omega_1\approx\omega_2 = \omega_0\]

Il en est alors de même pour les coefficients de qualité des circuits primaire et secondaire : \[Q_1=\frac{L_1~\omega_0}{R_1}~\approx~Q_2=\frac{L_2~\omega_0}{R_2}~=~Q\]

Comme pour le circuit oscillant série, nous allons calculer l’intensité pour une pulsation voisine de la pulsation de résonance.

Posons : \[\omega=\omega_0+\Delta\omega\qquad\text{et}\qquad\varepsilon=\frac{\Delta\omega}{\omega}\]

Tous calculs faits et en introduisant un nouveau paramètre : \[s=16~\varepsilon^2-8~\varepsilon^2~\Big(K^2-\frac{1}{Q^2}\Big)+\Big(K^2+\frac{1}{Q^2}\Big)^2\]

On obtient l’expression de \(I_2\) : \[I_2=\frac{M~\omega~U}{R_1~R_2~Q^2~\sqrt{s}}=\frac{K~U}{Q~\sqrt{R_1~R_2~s}}\]

3.2. Discussion

L’intensité \(I_2\) est minimale ou maximale quand la dérivée \(ds/d\varepsilon\) s’annule, c’est-à-dire : \[64~\varepsilon^3-16~\varepsilon~\Big(K^2-\frac{1}{Q^2}\Big)^2=0\]

3.2.1. Premier cas : \(K=1/Q\) ou \(K~Q=1\)

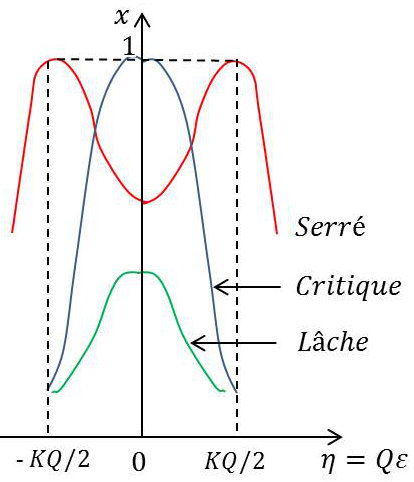Une seule racine (\(\varepsilon=0\)) annule la dérivée. On dit que le régime est critique.

On en déduit la valeur maximale de l’intensité \(I_{2c}\): \[I_{2c}=\frac{K~U}{Q~\sqrt{R_1~R_2}}~\frac{1}{2~K^2}=\frac{U}{2~\sqrt{R_1~R_2}}\]

En adoptant les notations du circuit oscillant : \[x=\frac{I_1}{I_{2c}}\quad;\quad\eta=Q~\varepsilon\]

On obtient : \[x=\frac{1}{\sqrt{1+4~\eta^2}}\]

Les pulsations de coupure qui correspondent à un affaiblissement de 3 dB, soit \(x=1/\sqrt{2}\), sont définies par la relation : \[1+4~\eta^2=2\qquad\Rightarrow\qquad\eta=\pm\frac{\sqrt{2}}{2}\]

D’où la largeur de bande (bande passante) : \[\Delta\Omega=\omega_2-\omega_1=\frac{\omega_0~\sqrt{2}}{Q}\]

La largeur de bande relative a pour valeur \(\sqrt{2}/Q\).

3.2.2. Deuxième cas : \(K>1/Q\) ou \(K~Q>1\)

Trois racines annulent la dérivée. On dit que le couplage est alors serré.

a) Une racine : \(\varepsilon=0\) ;

b) Deux racines : \[\varepsilon=\pm\frac{1}{2}~\sqrt{K^2-\frac{1}{Q^2}}~\approx~\pm\frac{K}{2}\]

La courbe présente deux valeurs maximales égales au maximum du régime critique et une valeur minimale.

3.2.3. Troisième cas : \(K<1/Q\) ou \(K~Q<1\)

Une seule racine (\(\varepsilon=0\)) annule la dérivée. La courbe présente la même forme que pour le régime critique (valeur maximale plus faible).

4. Application au filtrage

La courbe de réponse de deux circuits couplés à l’état critique a même allure que la courbe de réponse d’un circuit oscillant unique. Cependant, en ayant recours à une représentation graphique, on pourra remarquer que la réponse de deux circuits couplés rapproche davantage vers la forme idéale (créneau) que celle du circuit simple.

C’est la raison pour laquelle on utilise des circuits couplés pour transmettre des signaux dans une bande de fréquence déterminée. On peut donc dire que deux circuits couplés constituent grossièrement un filtre passe-bande.

Et l’on imagine déjà que pour affiner le processus et parvenir au filtre en tant que tel, il faudra associer un certain nombre de tels filtres passe-bande.