1. Introduction

Les molécules possèdent des propriétés différentes de celles des atomes qui la constituent, ce qui tient à la nature de la liaison chimique. Nous assimilerons le cristal à une molécule géante.

Les propriétés des solides peuvent être présentées en deux parties :

• certaines appartiennent en propre aux atomes qui constituent les cristaux ;

• d’autres, au contraire, dépendent de l’état de la matière, de la disposition de ses atomes.

Le fer par exemple n’a pas les mêmes comportements électrique ou magnétique à l’état liquide qu’à l’état de cristal. Comment et pourquoi les atomes de fer peuvent-ils se grouper pour former un cristal aux propriétés nouvelles que ses atomes constituants ne possèdent pas séparément ?

Le point de départ est donc l’atome dont la structure et les propriétés pourront être expliquées par la mécanique quantique.

2. Diffraction des rayons X. Rappels

Dans un milieu cristallisé, les atomes sont répartis régulièrement dans l’espace aux nœuds d’un réseau à trois dimensions.

On désigne par :

• \(d\) la distance séparant deux plans réticulaires ;

• \(\theta\) l’angle d’un rayon incident sur ces plans.

Bragg a montré que les directions de réflexion privilégiée sont données par : \[2~d~\sin\theta=p~\lambda\qquad (p=0,~1,~2,~\dots)\qquad[1]\]

Cette relation permet de connaître les directions de diffraction privilégiées des ondes \(X\) : \[\theta_1=\arcsin\frac{\lambda}{2~d}~~;~~\theta_2=\arcsin\frac{2~\lambda}{2~d}~~;~~\dots\qquad[2]\]

Le cas particulier le plus simple est celui de l’incidence normale (\(\theta=\pi/2\)).

La réflexion est alors assurée lorsque : \[2~d=p~\lambda\qquad\text{ou :}\quad\frac{2~\pi}{\lambda}=\frac{p~\pi}{d}\qquad[3]\]

Considérons à présent les ondes de Broglie de longueur d’onde \(\lambda=h/m~v\) associées à un électron de vitesse \(v\) dans le vide.

Cet électron a une quantité de mouvement : \[m~v=\frac{h}{\lambda}=\hbar~k\quad;\quad|\overrightarrow{k}|=\frac{2\pi}{\lambda}\quad(\text{vecteur d'onde})\]

L’énergie cinétique de l’électron est : \[E_{cin}=\frac{m~v^2}{2}=\frac{m^2~v^2}{2~m}=\frac{\hbar^2}{2~m}~k^2\qquad[4]\]

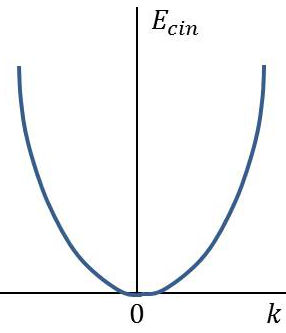Représentée en fonction de \(k\), c’est une parabole (\(k,E\)) aux propriétés physiques intéressantes (dérivées): \[\begin{aligned} \frac{\partial E}{\partial k}&=\frac{\hbar^2}{m}~k=\hbar~v \\ \frac{\partial^2E}{\partial k^2}&=\frac{\hbar^2}{m} \end{aligned} \qquad[5]\]

La pente de la courbe donne la vitesse de l’électron, ou la vitesse de groupe des ondes de Broglie qui l’accompagnent, et la courbure donne la masse \(m\) de l’électron libre.

3. Structure périodique du milieu cristallin n’intervenant pas

L’hypothèse que la structure périodique du milieu cristallin n’intervienne pas permet de considérer le problème sous l’angle de ce que l’on appelle l’approximation de Sommerfeld .

Un électron de charge \((-e)\) est soumis, de la part d’un ion positif de charge \((+q)\), placé en un nœud du réseau à une distance \((d)\), à une force d’attraction qui dérive d’un potentiel négatif de la forme : \[V=-k~\frac{e~q}{d}\qquad(k = cte)\qquad[6]\]

Nous faisons à cet effet deux hypothèses :

1. L’électron passe assez loin de chaque ion pour que l’on puisse remplacer la somme de tous les potentiels dus à tous les ions par une valeur moyenne négative et constante \(V_0\) dans le cristal et nulle en dehors. (En réalité, du fait que l’électron se déplace, cette somme varie)

2. Le réseau cristallin est simplifié, supposé linéaire, tous les ions étant placés à intervalles réguliers sur une droite \(Ox\).

L’équation de Schrödinger se réduit ici à : \[\frac{h^2}{8\pi^2~m}~\frac{d^2\psi(x)}{dx^2}+(W-V_0)~\psi(x)=0\qquad[7]\]

• \(m\) : masse de l’électron

• \(W\) : son énergie totale

• \(V_0\) : son énergie potentielle

• \(\psi(x)\) : onde de de Broglie accompagnant l’électron

Le cristal (ici un réseau linéaire) s’étend de \(x=0\) à \(x=L\).

Les conditions à imposer à la fonction \(\psi(x)\) pour que l’électron reste dans le cristal sont : \[\psi(0)=0\quad;\quad\psi(L)=0\]

Ces deux conditions imposent pour \(\psi\) une solution de la forme :

\[\begin{aligned} \psi(x)&=A~\sin(k~x)\\ k~L&=n~\pi\qquad (n\text{ entier})\end{aligned}\]

On en déduit la valeur de \(\cfrac{d^2\psi(x)}{dx^2}\) que l’on reporte dans (7), ce qui donne : \[W-V_0=\frac{h^2}{8\pi^2~m}=\frac{h^2~n^2}{8~m~L^2}\qquad[8]\]

Résultat très important :

Dans un cristal de dimensions finies, l’énergie totale \(W\) d’un électron ne pourra pas avoir de valeur arbitraire, mais devra être égale à l’une des valeurs : \[W=v_0+\frac{h^2n^2}{8~m~L^2}\qquad[9]\]

L’énergie des électrons libres dans ce réseau linéaire est donc quantifiée dans l’approximation de Sommerfeld. On peut dire encore qu’il existe pour des électrons libres dans un cristal non infini une suite de niveaux quantiques définis par (9). Suivant le principe d’exclusion de Pauli, chacun de ces niveaux peut être occupé au plus par deux électrons, de direction de spins opposées.

L’approximation de Sommerfeld qui attribue à \(V\) une valeur constante négative \(V_0\) dans tout le cristal n’a pas du tout tenu compte de la structure périodique de celui-ci. Elle nous a cependant montré qu’un électron libre dans un cristal fini ne peut avoir que des valeurs quantifiées de son énergie [9].

4. Structure périodique du milieu cristallin intervenant

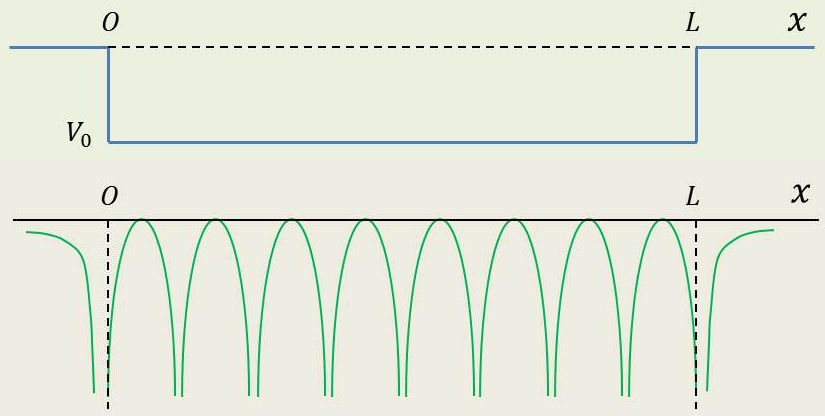Dans le cas où la structure périodique du milieu cristallin intervient, on substitue à la variation de \(V\) (fig. a) correspondant à l’approximation de Sommerfeld une variation périodique (fig. b), les minima de \(V\) correspondant au passage à proximité d’un ion positif.

Nous pouvons prévoir que, pour certaines valeurs de la longueur d’onde (\(\lambda\) de Broglie), donc pour certaines valeurs de \(v\) (\(\lambda=h/m~v\)) ou, ce qui revient au même, de l’énergie cinétique \(E_C\) des électrons, leurs ondes seront réfléchies totalement. Ceci revient à dire que pour certaines valeurs de leur énergie cinétique, les électrons ne pourront pas avancer dans le réseau, mais reviendront en arrière.

En réalité, ce ne sont pas des valeurs précises d’énergies, mais certains domaines d’énergie très étroits qui interdiront la propagation. Dans ces bandes d’énergie, dites bandes interdites, l’électron dont la valeur de l’énergie sera comprise dans une bande interdite ne pourra se propager dans le réseau. Il ne contribuera donc pas à la conductibilité électrique.

Le cristal se comporte en fait comme un filtre, ne laissant circuler que des électrons d’énergie située hors des bandes interdites.

L’équation de Schrödinger s’écrit ici : \[\frac{h^2}{8\pi^2~m}~\Delta\psi(\overrightarrow{r})+\{W-V(\overrightarrow{r})\}~\Delta\psi(\overrightarrow{r})=0\qquad (10)\]

• \(\overrightarrow{r}\) : vecteur joignant l’électron à l’origine des coordonnées

• \(W\) : énergie totale de l’électron

• \(V(\overrightarrow{r})\) : énergie potentielle de l’électron

• \(\Delta\psi(\overrightarrow{r})\) : onde de Broglie accompagnant l’électron

Lorsque l’électron circule dans le réseau cristallin, on doit s’attendre à ce que, par interaction avec les atomes disposés au nœud du réseau :

• la phase l’onde \(\psi\) soit, comme c’est toujours le cas, fonction de \(\overrightarrow{r}\) (facteur \(\exp i~(\overrightarrow{k}\cdot\overrightarrow{r})\)) ;

• l’amplitude l’onde \(\psi\) soit modulée par le déplacement dans le réseau : \[\psi(\overrightarrow{r})=u_{\overrightarrow{k}}(\overrightarrow{r})~\exp\{i~(\overrightarrow{k}\cdot\overrightarrow{r})\}\quad;\quad|\overrightarrow{k}|=\frac{2\pi}{\lambda}\qquad(\text{vecteur d'onde})\]

L’amplitude va varier avec la même périodicité que le réseau : en des points situés de manière identique à l’intérieur d’une maille du réseau, \(u\) reprend la même valeur.

Prenons le cas le plus simple possible : un réseau linéaire constitué d’atomes alignés régulièrement écartés d’une distance \(d\). \(V(\overrightarrow{r})\) va avoir une période spatiale égale à \(d\). L’onde de Broglie d’un électron va se comporter comme une onde \(X\) tombant normalement sur un cristal dont les plans réticulaires sont écartés de \(d\). Il y aura une réflexion totale lorsque : \[2~d=p~\lambda\qquad\text{ou :}\quad k=\frac{2~\pi}{\lambda}=\frac{p~\pi}{d}\]

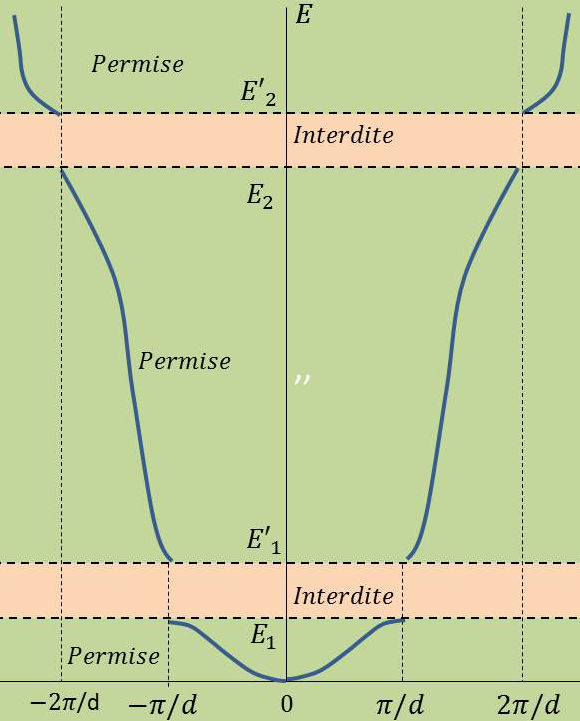La courbe représentant l’énergie cinétique \(E=W-V\) d’un électron en fonction de \(k\) n’est plus une parabole comme dans la propagation en espace libre. Elle se compose d’une succession d’arcs de courbes avec discontinuité pour les valeurs de \(k\) égales à : \[\pm\frac{\pi}{d},~\pm\frac{2\pi}{d},~\dots\]

Lorsque l’énergie prend des valeurs telles que \(E_1<E<E'_1\) ou bien : \(E_2<E<E'_2\), il y a réflexion totale des ondes de Broglie.

L’électron ne peut se propager dans le réseau linéaire. Les intervalles [\(E_1,~E'_1\)] et [\(E_2,~E'_2\)] constituent des bandes d’énergie interdites. La largeur \(E_1E'_1\) ou \(E_2E'_2\) dépend de l’expression du potentiel \(V(\overrightarrow{r})\).

Mais, dès que \(V(\overrightarrow{r})\) est périodique, les discontinuités apparaissent et la parabole relative à l’électron libre est remplacée par une succession d’arcs de courbe (voir la figure).

L’énergie d’un électron libre ne peut donc occuper que des valeurs comprises à l’intérieur d’un certain nombre de bandes permises, les valeurs comprises à l’intérieur des bandes interdites sont donc à exclure : aucun électron libre dans le solide ne peut les posséder.

Il faut remarquer qu’un cristal de dimensions usuelles comporte un très grand nombre de mailles du réseau et que la largeur d’une bande permise est très grande devant l’intervalle de deux énergies quantifiées consécutives correspondant à \(n\) et \(n+1\) (cf. 10).

Le nombre des niveaux d’énergie disponible dans chaque bande permise est extrêmement grand. Il faut trouver comment se répartissent les électrons :

• entre les différentes bandes permises ;

• à l’intérieur d’une bande permise donnée.