1. Schémas du MOS

Le transistor MOS est un transistor à effet de champ dans lequel la grille est séparée du canal par une mince couche d’oxyde, silice \(S_iO_2\).

Les transistors MOS industrialisés sont fabriqués avec du silicium.

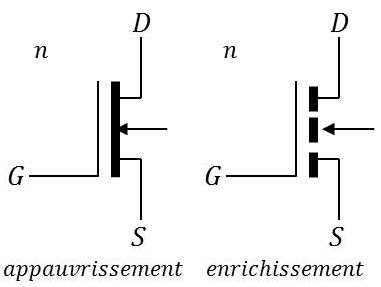
On distingue deux types de MOS :

• les MOS à canal préformé, dits à appauvrissement ;

• les MOS sans canal préformé, dits à enrichissement

Les deux symboles de MOS sont représentés dans le cas du canal dit de type N. Dans le cas du canal dit de type P, la flèche serait inversée.

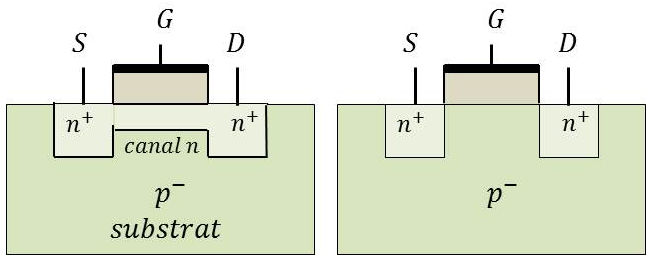
Les figures représentent la coupe d’un transistor MOS à canal N. La première correspond à un N diffusé, à appauvrissement. La deuxième correspond à un N non diffusé, à enrichissement.

2. Effet de surface d’une structure MIS

Nous considérons une simple structure MIS (métal – isolant semi-conducteur). La structure est de type P relié à la masse.

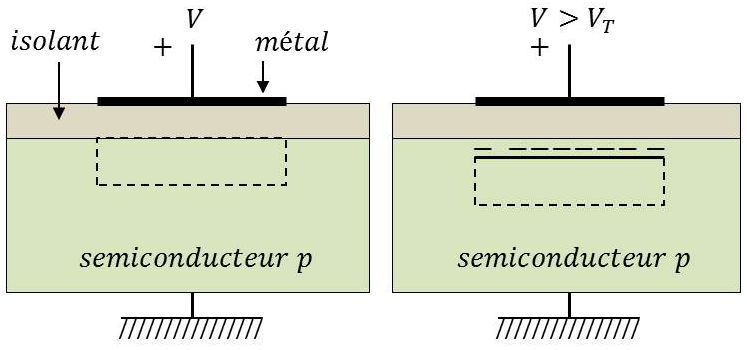L’application d’un potentiel positif \(V\), sur l’électrode métallique, provoque la création d’une zone vide de porteurs majoritaires (trous) à la surface du semi-conducteur sous l’électrode.

L’épaisseur de cette zone augmente avec la valeur de la tension \(V\).

Lorsque cette tension devient supérieure à une tension de seuil \(V_T\), il y a création, à la surface de la zone vide, d’une couche d’inversion. Il s’agit d’une couche contenant des porteurs minoritaires (électrons) dont l’épaisseur augmente avec la valeur de \(V\).

Cette couche d’inversion constitue ce que l’on appelle le canal N du transistor MOS à substrat P.

3. Théorie du transistor MOS. Caractéristiques courant / tension

Nous avons montré au paragraphe précédent que, lorsqu’on applique une tension positive suffisamment élevée à la grille d’un transistor MOS à substrat de type P, il y a formation d’une couche d’inversion sous l’oxyde : formation d’un canal de type N.

Considérons la structure du début sans canal diffusé. Une tension \(V_gs\) de seuil égale à \(V_T\) est nécessaire pour induire une couche d’inversion sous l’oxyde constituant le canal. Cette tension peut s’exprimer sous la forme : \[V_T=V_{FB}+2~(E_I-E_{FP})-\frac{Q_S}{C_{ox}}\qquad[1]\]

• \(C_{ox}\) : capacité d’oxyde par unité de surface

• \(Q_S\) : charge par unité de surface dans le canal

• \(V_{FB}\) : tension de bande plate

• \(E_{FP}\) : niveau de Fermi dans le substrat de type P

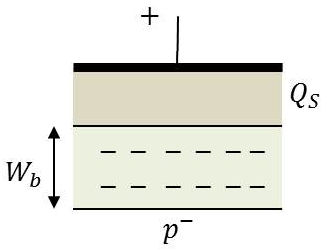Dans le canal, la concentration est constituée d’électrons libres et de charges fixes, négatives, correspondant aux atomes accepteurs ionisés. \[Q_S=Q_n+q~N_A~W_B\qquad[2]\]

• \(W_B\) : épaisseur de zone de charge d’espace (déserte en surface)

• \(N_A\) : concentration en impuretés du substrat de type P

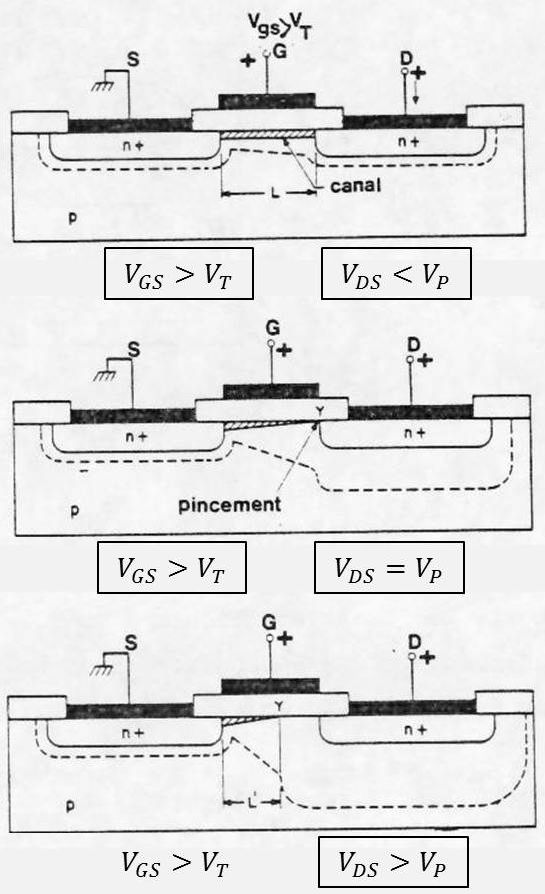Le fonctionnement du transistor MOS à canal N, pour \(V_{GS}>V_T\), est celui d’un transistor à effet de champ où \(V_{GS}>0\) (au lieu de \(V_{GS}<0\)).

Il existe dans le canal un champ électrique \(\overrightarrow{\varepsilon}\), orienté du drain vers la source, qui entraîne les électrons vers le drain, donnant naissance au courant de drain \(I_d\). Ces électrons proviennent de la source \(n^+\).

Comme dans un transistor à effet de champ, la largeur du canal est modulée par la tension \(V_{gs}\).

En un point \(x\) du canal, le potentiel est : \[V_{gx}=V_{gs}-V_{xs}\]

\(V_{gx}\) pouvant varier entre les deux limites : \[V_{gs}~~(x=0)\quad\rightarrow\quad V_{gs}-V_{gd}\quad(x=L)\]

Puisqu’un potentiel \(V_{gx}>0\) est nécessaire pour maintenir une couche canal d’inversion sous l’oxyde, l’épaisseur du canal diminue de la source vers le drain. On retrouve la tension maximale \(V_p\) (à \(V_g\) donné) pour laquelle le canal est pincé du côté drain. Parallèlement, la zone de charge d’espace se développe dans le substrat.

Comme pour le transistor à effet de champ, on peut calculer le courant drain par une méthode supposant des hypothèses simplificatrices. On aboutit à : \[I_d=\frac{\mu_n~Z~\varepsilon_i}{2~L~W_i}~(V_{gs}-V_T)^2=\frac{\mu_n~C_i}{2~L^2}~(V_{gs}-V_T)^2\qquad V_{ds}>V_{pincement}\qquad[3]\]

• \(\mu\) : mobilité moyenne des électrons en surface

• \(L,~Z\) : longueur et largeur du canal

• \(W_i,~\varepsilon_i,~C_i\) : épaisseur, constante diélectrique et capacité de l’isolant

On peut également calculer la transductance : \[g_m=\frac{I_d}{V_{gs}}=\frac{\mu_n~Z~\varepsilon_i}{2~L~W_i}~(V_{gs}-V_T)=\frac{\mu_n~C_i}{2~L^2}~(V_{gs}-V_T)\qquad[4]\]

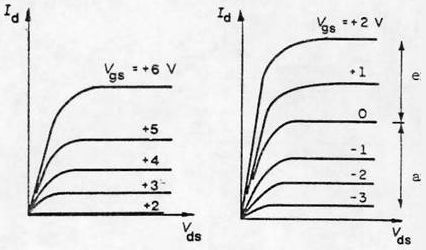Les caractéristiques courant / tension sont représentées ci-contre. Les premières sont relatives à un MOS sans canal N diffusé. Les deuxièmes sont relatives à un MOS avec canal N diffusé.

Dans le premier cas, le MOS est dit à enrichissement ; les caractéristiques partent de l’axe \(V_{ds}\) pour \(V_{gs}>V_T\). Dans le deuxième cas, il fonctionne pour \(V_{gs}>0\) et \(V_{gs}<0\).

Pour \(V_{gs}>0\), il est dit à enrichissement ; pour \(V_{gs}<0\), on retrouve le réseau d’un transistor à effet de champ.

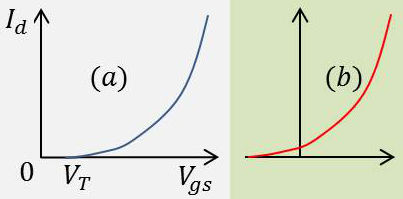Quand \(|V_{gs}|\) augmente, il y a dépeuplement du canal ; pour \(V_{gs}<0\), le MOS à canal diffusé est à appauvrissement.

La caractéristique de transfert, \(I_d(V_{gs})\) est tracée :

• (a) pour un MOS à canal N non diffusé ;

• (b) pour un MOS à canal N diffusé.

La pente de cette courbe en un point donne la transductance \(g_m\) : \[g_m=\frac{dI_d}{dV_{gs}}\]

4. Applications en logique CMOS

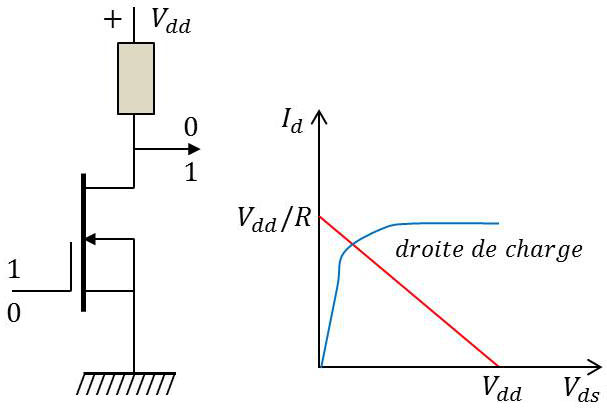Bien que ce type de dispositif connaisse quelques applications en amplification HF (absence de modulation), sa principale utilisation est dans les circuits logiques.

On voit en effet sur le schéma ci-contre qu’avec une seule tension d’alimentation, on peut véhiculer une information binaire.

Le MOS est chargé par une résistance R.

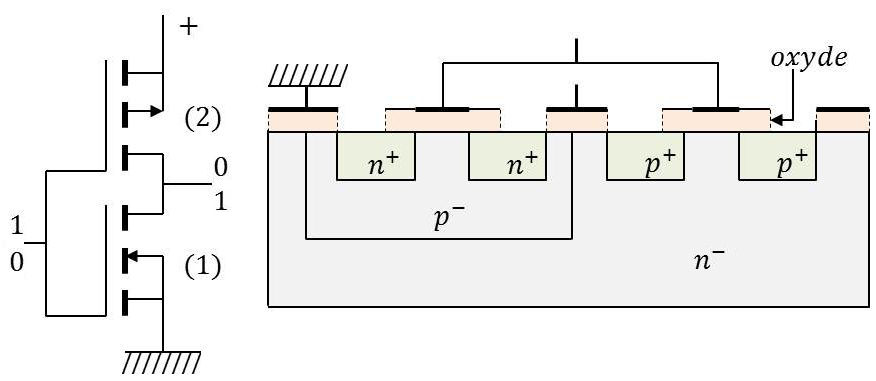L’utilisation de deux types de MOS, à canal P et à canal N (structure CMOS ou MOS complémentaire) permet de réaliser des circuits logiques sans consommation (sauf pendant les périodes de transition).

Quand (1) fonctionne, (2) est bloquée et réciproquement.

Les deux MOS de types opposés sont réalisés dans la même structure.

Et en dupliquant ce type de circuit, on peut obtenir un registre à décalage.