1. Thermoélectronique et thermoionique

1.1. Principe physique

Parler de tube électronique à notre époque peut paraître anachronique. Cependant, il n’en est rien, du moins pour certains spécialistes, notamment ceux de l’électronique à grande puissance et à grande fréquence.

Le principe du tube électronique est basé sur l’effet thermoélectronique appelé plus souvent, mais improprement effet thermoionique.

Rappelons-en brièvement le principe : Portés à une température élevée, les corps conducteurs émettent des électrons vers l’extérieur. Sous l’effet de cette agitation thermique, les électrons ont pu acquérir une énergie suffisante pour leur permettre de vaincre les forces qui les retiennent à l’intérieur du corps solide.

La quantité d’électrons émis dépend de l’énergie fournie aux électrons (ici par la température) et de l’importance des forces de liaison qui varient suivant la nature des corps. C’est là un problème de physique du solide.

1.2. Structure générale du tube électronique

Le tube électronique désigne un dispositif constitué par des électrodes placées dans une enceinte (généralement en verre) dans laquelle le vide a été fait (ce vide pouvant être remplacé par un gaz) et isolées entre elles. le système comprenant au moins une source d’électrons, L’ensemble est isolé de l’extérieur, mais les électrodes sont accessibles de l’extérieur par des terminaisons, passages étanches vers l’extérieur pratiqués dans le verre.

2. Diode à vide

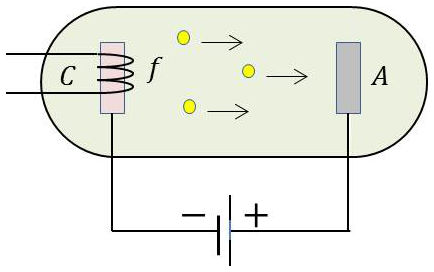La diode à vide est le premier élément à l’origine des dispositifs que nous allons étudier en nous reportant au schéma de la figure ci-contre.

Un fil conducteur C arrive à la cathode qu’un dispositif permet de chauffer localement(très souvent une résistance chauffante qui l’entoure). Une plaque métallique A appelée anode est portée à un potentiel positif par rapport à la cathode (batterie extérieure).

Si la cathode est suffisamment chauffée (le filament chauffant autour de la cathode la porte à une température d’environ 900 °C, température nécessaire pour obtenir une émission électrique suffisante), on constate le passage d’un courant dans le circuit : des électrons ont pu s’échapper de la cathode par effet thermoionique et ont été attirés par la plaque dont le potentiel est positif.

Du fait du vide, rien ne s’est opposé à ce déplacement ; les électrons atteignent la plaque alors que d’autres les remplacent dans la cathode. Inversons à présent les fils de la batterie ; le potentiel négatif de la plaque repousse les électrons thermo-ioniques, qui retombent sur la cathode : aucun courant ne circule alors dans le circuit extérieur.

La diode à vide constitue la base de tous les autres tubes. Sa découverte et son emploi en tant que détecteur (1904) ont fait faire un important progrès à la radioélectricité et ont permis la mise au point, quelques années plus tard, de la triode, qui a marqué la véritable naissance de l’électronique.

3. Triode

3.1. Principe

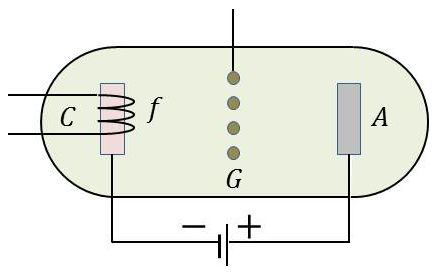Lee de Forest eut l’idée d’introduire une électrode intermédiaire G entre l’anode et la cathode, appelée grille en raison de sa forme de réseau de fils métallique. Une sorte de grillage permettant le passage des électrons.

Il était ainsi possible d’exercer une forme de commande du flux électronique. Lee de Forest avait obtenu un composant électronique capable d’amplification : la triode.

3.2. Réglages électriques

En prenant comme origine (0 V) le potentiel de la cathode, on porte la tension \(V_a\) de l’anode à une valeur comprise entre 100 et 300 V, la grille étant par ailleurs polarisée négativement, ce potentiel étant compris entre –10 et –2 V. De la sorte, la grille n’attire aucun électron et le courant de grille est nul.

En réalité, c’est le contraire qui se passe, la grille refoulant les électrons soit vers la cathode, soit vers un nuage que constitue la charge d’espace se créant autour de celle-ci.

Selon la valeur de la tension de polarisation négative qui lui est appliquée, la grille laissera passer entre ses mailles une portion des électrons qui s’échapperont vers l’anode. Il s’établit ainsi un courant anodique \(I_a\) de quelques milliampères qui est fortement fonction de la tension \(V_g\) et aussi, dans une bien moindre mesure, fonction de la tension d’anode \(V_a\).

3.3. Paramètres de la triode

Le premier paramètre est le coefficient d’amplification de la triode ou facteur \(\mu\), rapport entre les tensions \(V_a\) et \(V_g\), approximativement égal au rapport des capacités grille – cathode et anode – cathode (valeur comprise entre 15 et 100).

Le deuxième paramètre est l’influence de la tension grille sur le courant, à tension \(V_a\) constante. C’est la transductance ou encore la pente \(S\). Celle-ci se définit comme le rapport de la variation \(\Delta I_a\) du courant anodique \(I_a\) due à une variation \(\Delta V_g\) de la tension de grille : \[S=\frac{\Delta I_a}{\Delta V_g}\qquad[1]\]

Valeurs courantes  : 1,5 mA/V \(<S<\) 12 mA/V

D’autre part, si la tension grille est maintenue constante, \(I_a\) pourra varier d’une quantité \(\Delta I_a\) si on fait varier \(I_a\) de \(\Delta V_a\).

Le troisième paramètre qui en découle est la résistance interne du tube notée \(R_i\): \[R_i=\frac{\Delta V_a}{\Delta I_a}\qquad[2]\]

Pour de faibles valeurs de \(R_i\), le courant \(I_a\) dépendra fortement de \(V_a\).

Les valeurs courantes de \(R_i\) se situent entre 5 k\(\Omega\) et 50 k\(\Omega\).

On peut tirer la relation suivante (dite de Barkhausen) : \[\mu=S~R_i\qquad[3]\]

3.4. Détermination expérimentale des paramètres de la triode

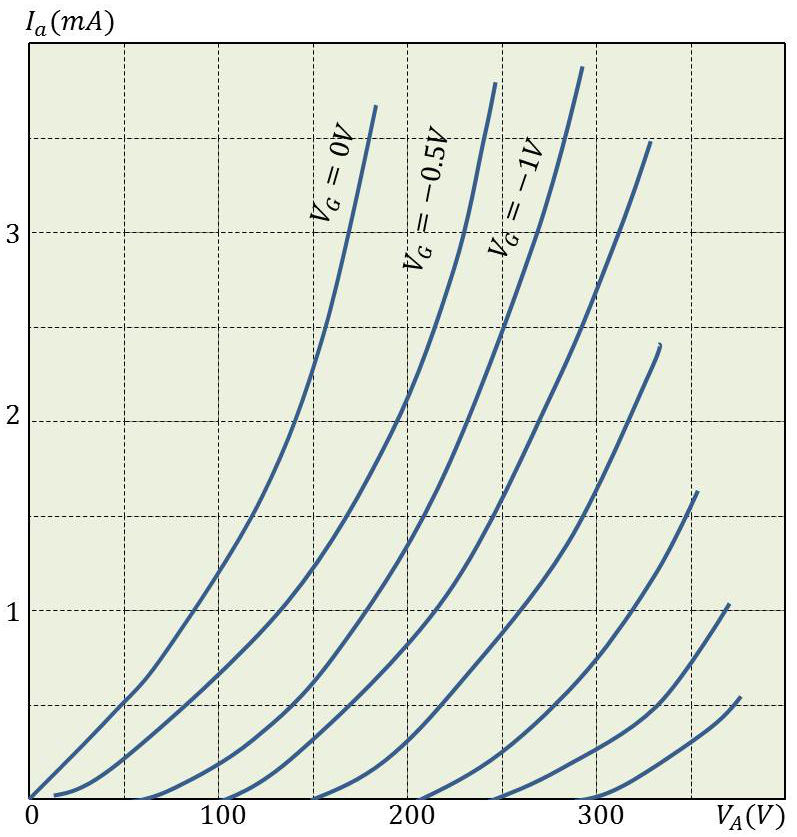La triode est caractérisée par un réseau d’abaques \(V_g(I_a,~V_a)\) fourni par le constructeur. Il s’agit de caractéristiques statiques.

On remarquera le parallélisme des courbes avec les variations vers des valeurs de plus en plus négatives de la tension de grille.

C’est à partir de ce réseau et compte tenu du point de fonctionnement que sont déterminés les trois paramètres du tube :

• la résistance interne \(R_a\) évaluée dans un domaine (voisinage d’un point de fonctionnement).

• le facteur d’amplification \(\mu\)

• la transductance \(S\)

3.4.1. Résistance interne \(R_i\)

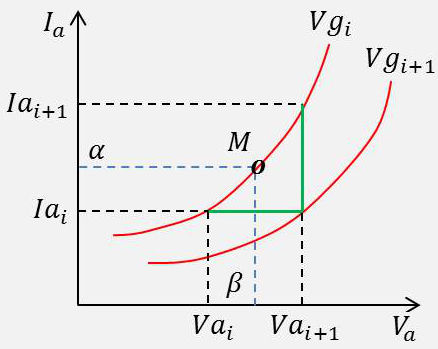Compte tenu de ce qui précède, la résistance d’anode \(R_a\) peut être obtenue à partir du réseau des courbes caractéristiques (figure ci-contre), \(M\) étant le point de fonctionnement choisi : \[[4]\qquad \begin{aligned} &R_i=\frac{\Delta V_a}{\Delta I_a}\\ &\Delta V_a=Va_{i+1}-Va_i\quad;\quad\Delta I_a=Ia_{i+1}-Ia_i \end{aligned}\]

Noter la différence notable avec la résistance au sens habituel du terme : \[R=\frac{\beta}{\alpha}\qquad[5]\]

3.4.2. Coefficient d’amplification \(\mu\)

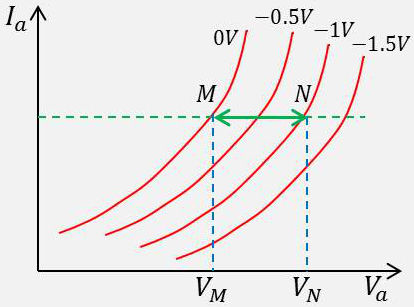Pour un courant d’anode donné, on suit sur le réseau, une variation de potentiel de grille (ici \(\Delta V_g=1~\rm V\) du point \(M\) au point \(N\)). D’où une variation du potentiel d’anode.

D’où le facteur d’amplification \(\mu\) : \[\mu=\frac{\Delta V_a}{\Delta V_g}\qquad[6]\]

3.4.3. Transductance \(S\)

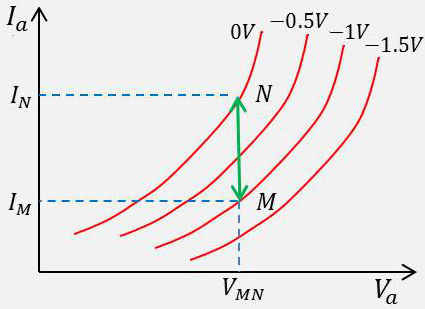Pour une tension d’anode fixée, on détermine la variation du courant d’anode en fonction de la variation des potentiels de grille.

D’où le facteur de transductance \(S\), (inverse d’une résistance) : \[S=\frac{\Delta I_a}{\Delta V_g}\qquad\text{exprimée en}~\Omega^{-1}\qquad[7]\]

3.5. Remarques concernant le fonctionnement

Nous raisonnerons sur un exemple pratique en faisant l’hypothèse des valeurs suivantes des paramètres (tube fonctionnant en amplificateur) : \[S=3~\rm{mA~V^{-1}}\quad;\quad R_i=20~\rm k\Omega\quad\Rightarrow\quad\mu=60\]

On suppose que le point de fonctionnement a été déterminé dans les conditions : \[V_g=3~\rm{V}\quad;\quad V_a=200~\rm{V}\quad;\quad I_a=4~\rm mA\]

Avec une tension d’entrée \(V_g=1~\rm V\), le courant sera \(I_a=S~V_g=3~\rm mA\). Et si on intercale une résistance \(R_a=1~\rm k\Omega\) en série entre l’anode et sa source, la tension aux bornes de cette résistance due au passage du courant sera de 3 V. Ainsi, dans un tel circuit, le coefficient d’amplification, ou son gain en tension, est égal à 3.

Il peut paraître facile d’augmenter le gain en choisissant des résistances plus grandes. Avec \(R_a=10~\rm k\Omega\), on pourrait penser obtenir une tension de sortie de 30 V. Il n’en est rien et on trouvera une tension de 20 V. Cela provient de ce que la chute de tension dans la résistance \(R_a\) constitue elle-même une variation appréciable de la tension anodique \(V_a\) et, par suite de l’existence de la résistance du tube \(R_i\), cette variation agit en sens inverse de la variation initiale du courant \(I_a\).

Si la valeur de la résistance \(R_a\) n’est pas faible, comparée à celle de \(R_i\), l’effet de la résistance interne ne peut plus être négligé. Par conséquent, le gain en tension qu’on peut atteindre est limité aux valeurs de \(\mu\) qui peuvent être approchées en rendant aussi grande que possible la valeur de \(R_a\) par rapport à \(R_i\).

4. Utilisation de la triode

4.1. Montage de principe

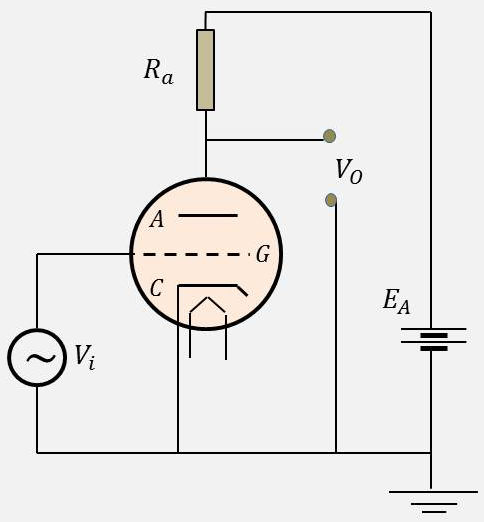Le montage de principe d’une triode est représenté figure ci-contre.

• \(V_i\) et \(V_0\) sont les tensions alternatives respectives d’entrée et de sortie(signaux utiles) ;

• \(E_A\) est la tension continue d’alimentation (polarisation de l’anode et de la cathode) ;

• \(R_a\) est la résistance de charge montée en série avec l’anode.

Dans ce qui suit, nous verrons sur un exemple pratique (à titre d’exercice) comment est disposée la triode amplificatrice dans un circuit avec son schéma équivalent.

4.2. Application classique

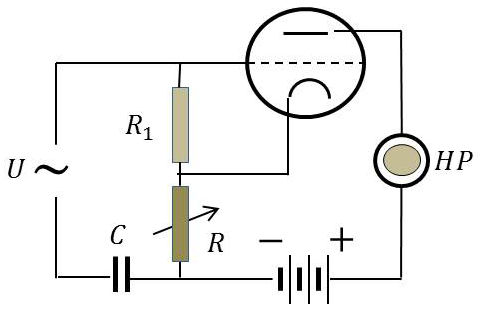Pour mesurer le coefficient d’amplification \(\mu\) d’un tube électronique, on réalise le montage ci-après.

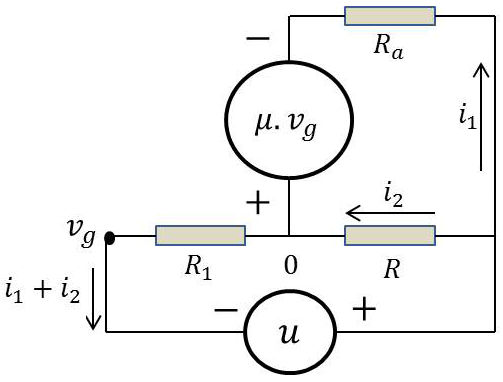
Trouver l’expression de \(\mu\) en fonction des données lorsqu’aucun son n’est perçu dans l’écouteur. On négligera l’impédance de \(C\).

Réponse :

On dessine le schéma équivalent et on écrit les équations nécessaires . On détermine ainsi \(i_1,~i_2,~v_g\).

Noter le potentiel \(v_g\).

Par application de la loi des mailles (3 mailles) :

\[\begin{aligned} &(1)\quad~~~~v_g=-(i_1+i_2)~R_1\\ &(2)\quad~~~~~~u=R_1~i_1+(R_1+R)~i_2\\ &(3)\quad~~\mu~v_g=-R_a~i_1-R~i_2\end{aligned}\]

Si \(i_1=0\), les relations (1) et (3) donnent : \[v_g=-R_1~i_2\quad;\quad \mu~v_g=-R~i_2\]

Il s’ensuit que : \[\mu=\frac{R}{R_1}\]