1. Exercice 1

1.1. Énoncé

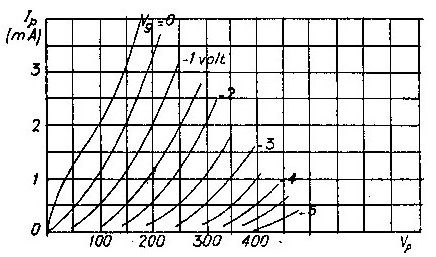On considère les caractéristiques \((V_p~;~I_p)\) d’une lampe triode (figure ci-contre).

Les conditions de fonctionnement sont les suivantes : \[V_g=-1,5~{\rm V}\quad;\quad V_p=200~\rm V\]

Quelles sont, dans ces conditions, les valeurs de la pente \(S\) et de la résistance interne \(r_p\) ?

En déduire le coefficient d’amplification \(K\).

1.1.1. Réponse

Le point de fonctionnement correspondant pratiquement (voir le réseau) à \(I_p\cong 1,4~mA\) Considérant sur le réseau les variations "autour de ce point de fonctionnement" on définit les paramètres

\[\begin{aligned} S&=\frac{\Delta I_p}{\Delta V_g} &&\text{pente}\\ r_p&=\frac{\Delta V_p}{\Delta I_p} &&\text{résistance interne (ou de plaque)}\\ K&=\frac{\Delta V_p}{\Delta V_g}=S~r_p &&\text{coeff. d'amplification}\end{aligned}\]

1) Pour \(V_g\) entre –2 V et –1 V :  \(\Delta I_p=\)1,5 mA. On a donc : \(S=1,5~\rm mA~V^{-1}\).

2) On passe horizontalement de la courbe à \(V_g\) = –1,5 V à la courbe voisine \(V_g\) = –2 V. Il s’ensuit un déplacement de \(V_p\) = 200 V à \(V_p\) = 250 V.

Sur la verticale en \(V_p=\) 250 V, un point \(I_p\) = 2 V sur la courbe \(V_g\) = –1,5 V.

On peut estimer que \(\Delta I_p\) = 0,7 mA. On a donc \(r_p=70~\rm k\Omega\).

3) \(K=S~r_p~\approx~105\).

2. Exercice 2

2.1. Énoncé

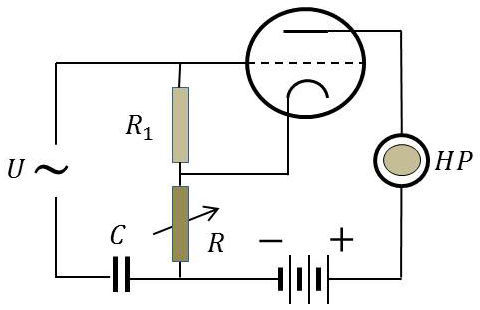Pour mesurer le coefficient d’amplification \(K\) d’un tube électronique, on réalise le montage ci-contre.

Trouver l’expression de \(K\) en fonction des données lorsqu’aucun son n’est perçu dans l’écouteur. On négligera l’impédance de \(C\).

2.2. Réponse

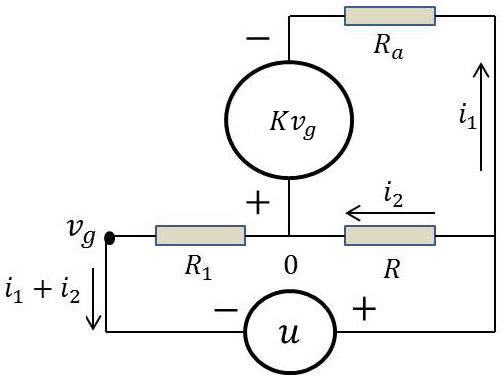Le schéma équivalent est représenté figure ci-contre.

Écrivons les équations des mailles (3 relations). On obtient respectivement :

\[\begin{aligned} v_g&=-R_1~(i_1+i_2)\\ u&=R_1~i_1+(R+R_1)~i_2\\ K~v_g&=r_p~i_1-R~i_2\end{aligned}\]

Aucun son ne passe dans l’écouteur : \(i=0\).

Cette simplification étant : \[v_g=-R_1~i_2\quad;\quad K~v_g=-R~i_2\]

Par suite : \[K=\frac{R}{R_1}\]

3. Exercice 3

3.1. Énoncé

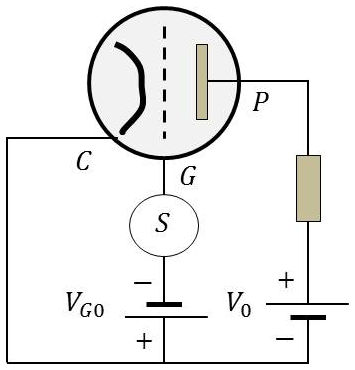1) On considère une triode dont on connaît trois points de fonctionnement :

\[\begin{aligned} &(1)~~V_a=300~{\rm V} &&V_g=-3~{\rm V} &&I_a=7~\rm mA\\ &(2)~~V_a=300~{\rm V} &&V_g=-2~{\rm V} &&I_a=8~\rm mA\\ &(3)~~V_a=250~{\rm V} &&V_g=-3~{\rm V} &&I_a=2~\rm mA\end{aligned}\]

Déterminer les coefficients \(K,~\rho,~U\) de la formule : \[\rho~I_a=K~V_g+V_a+U\]

ainsi que la valeur de la pente \(S\).

2) On place une résistance \(R\) dans le circuit plaque. Dans le circuit grille se trouve un générateur alternatif et une polarisation fixe : \[V_g=V_{g0}+s_m~\sin~\omega~t\]

Il s’ensuit un courant de plaque : \[I_a=I_0+i_m~\sin~\omega~t\]

3) Donner l’expression du rendement \(\eta\), rapport de la puissance alternative dépensée dans la résistance \(R\) à la puissance totale.

3.2. Réponse

1) En portant les données sur un diagramme \((V_a,~I_a)\) :

\[\begin{aligned} \rho&=\Big(\frac{\Delta V_a}{\Delta I_a}\Big)_{Vg=cte}=10~\rm k\Omega &&\text{résistance interne}\\ S&=\Big(\frac{\Delta I_a}{\Delta V_g}\Big)_{Va=cte}=10^{-3}~\rm A~V^{-1} &&\text{pente}\end{aligned}\]

On en déduit (coefficient d’amplification : \[K=\rho~S=10\]

En revenant à l’expression (courant de maille) : \[\rho~I_a=K~V_g+V_a+U\]

On obtient \(U\) = –200 V.

2) En effectuant les substitutions dans l’équation de maille : \[(R+\rho)~(I_0+i_m~\sin\omega~t)=K~(V_{g0}+s_m~\sin\omega~t)+V_a+U\]

En identifiant les parties respectivement continue et alternative :

\[\begin{aligned} (\rho+R)~I_0&=K~V_{g0}+V_a+U\\ i_m&=\frac{K.s_m}{(\rho+R)}\end{aligned}\]

D’où l’expression du gain : \[G=-\frac{K~R}{\rho+R}\]

Note : La valeur minimum qu’il faut donner à \(V_{g0}\) pour que (\(V_{g0}+s_m\sin\omega t\)) reste toujours négatif est évidemment : \(V_{g0}\leq -s_m\).

3) On utilisera les deux relations (partie continue et partie alternative) exprimées précédemment ainsi que :

– la puissance (alternative) dissipée dans \(R\) : \[P_d=\frac{1}{2}~R~i_m^2\]

– la puissance totale : \[P_t=R~I_0^2+\frac{1}{2}~R~i_m^2\]

On obtient pour le rendement : \[\eta=\frac{P_d}{P_t}=\frac{1}{1+\cfrac{1}{2}~(V_{g0}+s_m)^2}\]

\(\eta\) passe par un maximum égal à \(1\) pour \(V_{g0}=-s_m\).