1. Osculation d’un réseau cristallin

1.1. Énoncé

1) Les électrons d’un faisceau cathodique d’une intensité de 0,16 mA ont acquis une vitesse de 60 000 km/s. Elles rencontrent une plaque de platine de 5 g.

En admettant que les \(9/10\) de la puissance reçue par la plaque sont transformés en chaleur, calculer la température atteinte par la plaque après une minute de bombardement cathodique, en supposant le refroidissement négligeable.

2) Quelle est la longueur d’onde minimum \(\lambda_0\) des rayons \(X\) issus de l’anticathode ?

3) Un faisceau parallèle de ces rayons \(X\) tombe sur un cristal de chlorure de sodium NaCl dont les centres réfringents Na\(^+\) et Cl\(^-\) jouent le même rôle et se situent aux sommets de cubes superposés.

Calculer la distance des plans réticulaires du réseau, sachant que le cristal a une masse moléculaire \(M\) = 54,45 g et une masse spécifique \(\rho\) = 2,16 g/cm\(^{-3}\).

On donne :

• Masse de l’électron : \(m~=~1,10\times 10^{-30}~\rm kg\)

• Charge de l’électron : \(q~=~1,602\times 10^{-19}~\rm C\)

• Nombre d’Avogadro : \(N~=~6,025\times 10^{-23}~\rm mole^{-1}\)

• Constante de Planck : \(h~=~6,62\times 10^{-34}~\rm m^2~kg~s^{-1}\)

• Vitesse de la lumière : \(c~=~3\times 10^8~\rm m~s^{-1}\)

• Chaleur spécifique du platine : \(C_{\rm Pt}~=~130~\rm J~kg^{-1}~K^{-1}\)

1.2. Réponse

1) On calcule d’abord l’énergie des électrons : \[E~=~m~c^2~=~\frac{m_0~c^2}{\sqrt{1-\beta^2}}\qquad;\qquad\beta=\frac{v}{c}=0,2\]

On effectue le développement limité : \[\frac{1}{\sqrt{1-\beta^2}}~\approx~1+\frac{0,04}{2}+\dots~\approx~1,02\]

La fraction d’énergie perdue dans le platine sera une fraction de l’énergie cinétique \(E_c\) : \[E_c~=~m_0~c^2~(1,02-1)\]

Tous calculs faits : \[E_c~=~18\times 10^{-16}~\rm J\]

Énergie exprimée en électron-volts en divisant par la charge de l’électron : \[E_c~=~11,25~\rm keV\]

Les électrons sont donc accélérés par une d.d.p. : \[U~=~11~250~\rm V\]

Le faisceau transporte 0,16 mA, c’est-à-dire une charge de 0,16 mC/s. Ce qui correspond à un nombre d’électrons : \[N~=~\frac{0,16\times 10^{-3}}{1,6\times^{-19}}~=~10^{15}\]

D’où une énergie cinétique totale par seconde : \[W~=~N_e~E_c~=~1,8~\rm J\]

Soit, par minute : \[W'~=~1,8\times 60~=~108~\rm J\]

Quantité d’énergie perdue dans le plateau en une minute : \[W''~=~108\times\frac{9}{10}~=~97,2~\rm J\]

D’où l’élévation de température pour les 5 grammes de platine : \[\Delta\theta~=~\frac{W''}{C_{\rm Pt}~m_{\rm Pt}} ~=~\frac{97,2}{130\times 5\times 10^{-3}}=149~\rm K\]

2) En introduisant l’énergie élémentaire de l’électron (formule d’Einstein) : \[\lambda_0~=~\frac{c}{\nu}~=~\frac{h~c}{h~\nu} ~=~\frac{(6,62\times 10^{-34})~(3\times 10^8)}{18\times 10^{-16}}~=~1100~\rm \mu m\quad(rayons X)\]

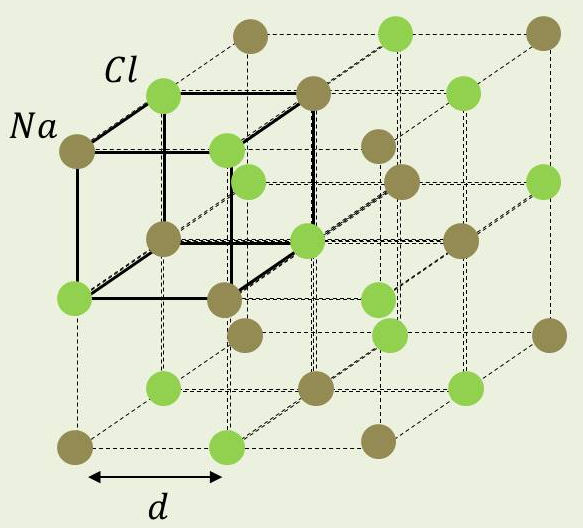3) On considère un cube élémentaire formé de 4 molécules de NaCl et dont l’arête a une longueur \(d\).

Pour que ce cube remplace exactement un cube identique, il faut lui faire subir dans une des trois directions perpendiculaires entre elles une translation de \(2~d\).

Par suite, les 4 molécules de NaCl occupent un volume égal à \(8~d^3\), soit \(2~d^3\) par molécule.

On peut dire que chaque molécule a une masse de : \[\frac{58,45}{6,02\times 10^{23}}~\rm g\qquad\text{ou encore}\qquad\{2~d^3\times 2,16~\}~g\]

D’où : \[d^3~=~22,45\times 10^{-24}~{\rm cm^3}\qquad\Rightarrow\qquad d~=~2,82\times 10^{-10}~\rm m~=~0,282~nm\]

2. Groupe de symétrie

2.1. Énoncé

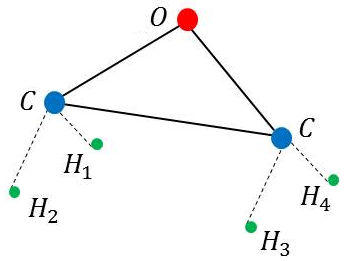On veut étudier les symétries de la molécule d’oxyde d’éthylène \(\rm C_2H_4O\) représentée à la figure ci-contre.

1) Sans identifier les atomes d’hydrogène (indices,) mettre en évidence les axes de coordonnées.

2) En tenant compte cette fois des indices, caractériser les différentes opérations de symétrie.

3) Construire la table de multiplication des opérations de symétrie.

2.2. Réponse

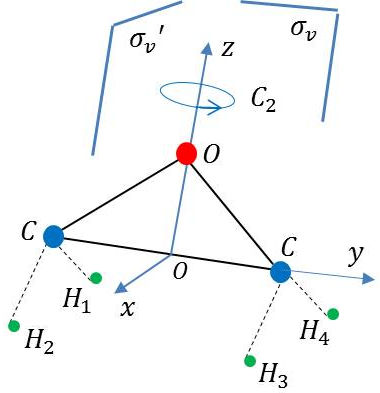1) La figure ci-contre met en évidence la géométrie de la molécule (axes de coordonnés \(Oxyz\)).

2) Identification des symétries

• Élément identité \(E\).

• Rotation de \(\pi\) autour de l’axe \(Oz\) : \[\rm H_4~\leftrightarrow~H_2~~\qquad\text{et}\qquad H_3~\leftrightarrow~H_1\]

• Miroir \(\sigma_v\) représenté par le plan \(\{0zy\}\) : \[\rm H_2~\leftrightarrow~H_1~~\qquad\text{et}\qquad H_3~\leftrightarrow~H_4\]

• Miroir \(\sigma_v'\) représenté par le plan \(\{0zx\}\) : \[\rm H_2~\leftrightarrow~H_3~~\qquad\text{et}\qquad H_1~\leftrightarrow~H_4\]

3) Construction de la matrice

Un résultat évident.

Les deux plans de symétrie étant orthogonaux, une séquence des deux transformation conduit à une rotation de \(\pi\) autour de l’axe commun : \[\sigma_v\times\sigma_v'=C_2=\sigma_v'\times\sigma_v\]

Il est également évident que : \[(C_2)^2=(\sigma_v)^2=(\sigma_v')=E\]

D’autres raisonnements de ce type sont possibles.

D’une manière générale, on essaie toutes les combinaisons géométriques possibles.

D’où la structure de la matrice (opération de départ en ligne horizontale, résultat de la combinaison en première colonne) : \[\begin{matrix} &\textbf{2~/~1}& &\textbf{E}& &C_2& &\sigma_v& &\sigma_v'\\ &\textbf{E}& &E& &C_2& &\sigma_v& &\sigma_v'\\ &C_2& &C_2& &E& &\sigma_v'& &\sigma_v\\ &\sigma_v& &\sigma_v& &\sigma_v'& &E& &C_2\\ &\sigma_v'& &\sigma_v'& &\sigma_v& &C_2& &E \end{matrix}\]

3. Vibrations

3.1. Énoncé

Une technique de comparaison des constantes de force (liaison) entre deux molécules :

• acide chlorhydrique {\(\rm H-Cl\)} ;

• monoxyde de carbone {\(\rm C=O\)}.

1) Rappeler les deux formules relatives aux niveaux d’énergie : harmonique et anharmonique (approximation de Morse).

2) On a mesuré la longueur d’onde correspondant à la fréquence de vibration pour la molécule {\(\rm H-Cl\)} et on a obtenu la valeur \(\lambda=3,33~\rm \mu m\).

En déduire la constante \(k\) de force de liaison dans cette molécule.

3) On considère à présent la molécule de {\(\rm C=O\)}.

On a noté deux transitions dans le domaine infrarouge :

• \(\lambda_1~=~4,67\times 10^{-6}~\rm m\)

• \(\lambda_2~=~2,35\times 10^{-6}~\rm m\)

4) Une conclusion ?

Données :

\[\begin{aligned} c&=3\times 10^8~\rm m~s^{-1} \\ m_{\rm Cl}&\approx 35 &&\text{ou encore}~:\quad m_{\rm Cl}=5,814\times 10^{-26}~\rm kg \\ m_{\rm H}&\approx 1 &&\text{ou encore}~:\quad m_{\rm H}=0,166\times 10^{-26}~\rm kg\\ m_{\rm C}&\approx 12 &&\text{ou encore}~:\quad m_{\rm C}=1,993\times 10^{-26}~\rm kg\\ m_{\rm O}&\approx 16 &&\text{ou encore}~:\quad m_{\rm O}=2,656\times 10^{-26}~\rm kg\end{aligned}\]

3.2. Réponse

1) Les deux formules de l’énergie \(E_v\) (resp. harmonique et anharmonique) :

\[\begin{aligned} &E_v~=~\Big(v+\frac{1}{2}\Big)~h~\nu_{osc} &&(1)\\ &E_v~=~\Big\{\Big(v+\frac{1}{2}\Big)~-~x_e~\Big(v+\frac{1}{2}\Big)^2\Big\}~h~\nu_{osc} &&(2)\end{aligned}\]

2) Calcul de la fréquence des oscillations : \[\nu_{osc}~=~\frac{1}{\lambda}~=~9\times 10^{-13}~\rm Hz\]

On sait que : \[\nu_{osc}~=~\frac{1}{2\pi}~\sqrt{\frac{k}{\mu}}\]

Calcul de la masse réduite : \[\mu~=~\frac{m_{\rm Cl}~m_{\rm H}}{m_{\rm Cl}+m_{\rm H}}~=~1,6\times 10^{-27}~\text{kg / molécule}\]

Et tous calculs faits : \[k~=~4\pi^2~\mu~\nu_{osc}^2~=~515~\rm N~m^{-1}\]

3) À partir de la relation (2), et y faisant respectivement {\(v=1,0~;~2,0\)}, on obtient pour l’énergie des deux transitions : \[\left\{ \begin{aligned} E_1-E_0~=~(1-2~x_e)~h~\nu_{osc}~=~\frac{h~c}{\lambda_1}\\ E_2-E_0~=~(2-6~x_e)~h~\nu_{osc}~=~\frac{h~c}{\lambda_2} \end{aligned} \right.\]

qui conduit à la relation : \[\frac{1-2~x_e}{1-6~x_e}~=~\frac{\lambda_2}{\lambda_1}~\approx 0,5\]

et tous calculs faits, pour le facteur anharmonique : \(x_e~\approx~0,006\)

On détermine ensuite la fréquence des oscillations en revenant, par exemple, à la première des deux relations : \[\nu_{osc}~=~\frac{1}{\lambda_1}~\frac{1}{1-2~x_e}~=~6,5\times 10^{13}~\rm Hz\]

Et comme dans la première partie : \[k~=~4\pi^2~\mu~\nu_{osc}^2\]

Avec, pour la masse réduite : \[\mu~=~\frac{m_{\rm C}\times m_{\rm O}}{m_{\rm C}+m_{\rm O}}~=~1,4\times 10^{-27}~\text{kg / molécule}\]

Application numérique : \(k~=~1900~\rm N~m^{-1}\)

4) On voit que la constante de force \(k_2\) pour une double liaison \(\rm C=O\) est plus importante (ici presque 4 fois) que la constante de force \(k_1\) dans le cas d’une liaison simple \(\rm H-Cl\). Ce qui semble tout à fait logique.