1. Pendule

1.1. Exercice 1. Pendule composé

1.1.1. Énoncé

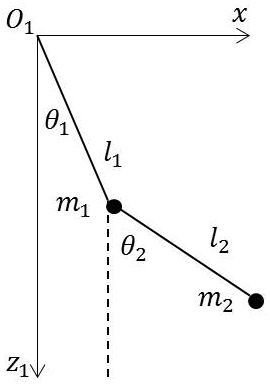Un premier pendule simple (masse \(m_1\), longueur \(l_1\)) peut faire de petites oscillations autour de l’axe \(O_1\) dans un plan vertical pris comme plan du tableau.

Un deuxième pendule simple (masse \(m_2\), longueur \(l_2\)) peut osciller dans le même plan. Son axe de rotation \(O_2\) coïncide avec la masse \(m_2\).

On désignera par \(\theta_1\) et \(\theta_2\) les écarts angulaires avec la verticale.

Établir les équations différentielles des petits mouvements des masses \(m_1\) et \(m_2\) :

1. en utilisant les équations de Lagrange ;

2. en application du théorème de d’Alembert (par les forces appliquées).

1.1.2. Solution

1) En utilisant les équations de Lagrange

a) Nous faisons l’hypothèse de petits mouvements autour de la position d’équilibre : \[\left\{ \begin{aligned} &x_1=l_1~\sin\theta_1\approx~l_1~\theta_1\\ &z_1=l_1~\cos\theta_1\approx~l_1~\Big(1-\frac{\theta_1^2}{2}\Big) \end{aligned} \right.\] \[\qquad\qquad\qquad~~~~ \left\{ \begin{aligned} &x_2=x_1+l_2~\sin\theta_2=l_1~\theta_1+l_2~\theta_2\\ &z_2=z_1+l_2~\cos\theta_2=l_1~\Big(1-\frac{\theta_1^2}{2}\Big)+l_2~\Big(1-\frac{\theta_2^2}{2}\Big) \end{aligned} \right.\]

b) Énergie potentielle \(U\) (travail fourni pour déplacer les deux masses)

Rappel de l’expression de l’énergie potentielle du pendule simple (petits mouvements) : \[U=m~g~l~\frac{\theta^2}{2}\]

Dans le cas présent (deux masses) : \[2~U=2~U_1+2~U_2=m_1~g~l_1~\theta_1^2+m_2~g~(l_1~\theta_1^2+l_2~\theta_2^2)\]

Ou encore : \[2~U=(m_1+m_2)~g~l_1~\theta_1^2+m_2~g~l_2~\theta_2^2\]

c) Énergie cinétique \(W\)

Expression des vitesses : \[\begin{aligned} &v_1=\frac{dx_1}{dt}=l_1~\frac{d\theta_1}{dt}\\ &v_2=\frac{dx_2}{dt}=l_1~\frac{d\theta_1}{dt}+l_2~\frac{d\theta_2}{dt} \end{aligned}\]

Rappel de l’expression pour l’ensemble des deux masses : \[W=W_1+W_2=\frac{1}{2}~m_1~v_1^2+\frac{1}{2}~m_2~v_2^2\]

Tous calculs faits, on obtient : \[2~W=(m_1+m_2)~l_1^2~\Big(\frac{d\theta_1}{dt}\Big)^2+2~m_2~l_1~l_2~\frac{d\theta_1}{dt}~\frac{d\theta_2}{dt}+m_2~l_2^2~\Big(\frac{d\theta_2}{dt}\Big)^2\]

d) Équations de Lagrange : \[\qquad\qquad\qquad [1]\qquad \left\{ \begin{aligned} &\frac{d}{dt}\Big(\frac{\partial W}{\partial\theta_2'}\Big)+\frac{\partial U}{\partial\theta_1}=0\\ &(m_1+m_2)~l_1^2~\frac{d^2\theta_1}{dt^2}+m_2~l_1~l_2~\frac{d^2\theta_2}{dt^2}+(m_1+m_2)~g~l_2~\theta_1=0 \end{aligned} \right.\] \[[2]\qquad \left\{ \begin{aligned} &\frac{d}{dt}\Big(\frac{\partial W}{\partial\theta_1'}\Big)+\frac{\partial U}{\partial\theta_2}=0\\ &m_2~l_2^2~\frac{d^2\theta_2}{dt^2}+m_2~l_1~l_2~\frac{d^2\theta_1}{dt^2}+m_2~g~l_2~\theta_2=0 \end{aligned} \right.\]

Toutes simplifications faites, respectivement par \(l_1\) dans le premier groupe et \(l_2\) dans le deuxième puis combinant [1] et [2], il vient, tous calculs faits, pour les équations différentielles, respectivement en \(\theta_1\) et \(\theta_2\) : \[\begin{aligned} &m_1~l_1~\frac{d^2\theta_1}{dt^2}+(m_1+m_2)~g~\theta_1=m_2~g~\theta_2\qquad\qquad~~~~(1)\\ &m_1~l_2~\frac{d^2\theta_2}{dt^2}+(m_1+m_2)~g~\theta_2=(m_1+m_2)~g~\theta_1\qquad(2) \end{aligned}\]

2) En application du théorème de d’Alembert

a) Équilibres des forces et relations du triangle (voir figure) \[\overrightarrow{m_1~g}=\overrightarrow{X_1}+\overrightarrow{T_1}\]

Les relations du triangle : \[\frac{X_1}{\sin\theta_1}=\frac{m_1~g}{\cos\theta_1}\quad\Rightarrow\quad X_1=m_1~g~\theta_1\]

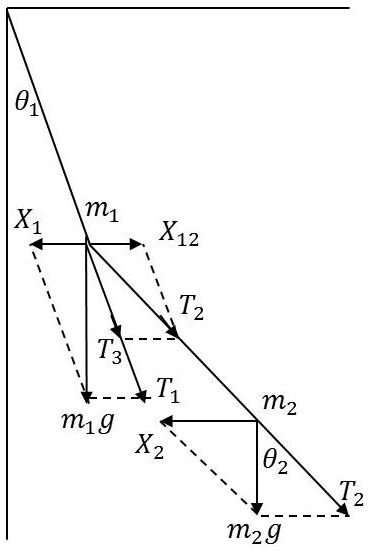Équilibre de forces : \[\overrightarrow{m_2g~}=\overrightarrow{X_2}+\overrightarrow{T_2}\]

Relations du triangle : \[\begin{aligned} \frac{X_2}{\sin\theta_2}=\frac{m_2~g}{\cos\theta_2}=\frac{T_2}{\sin(\pi/2)} \end{aligned} \Rightarrow \left\{ \begin{aligned} &X_2=m_2~g~\theta_2\\ &T_2=m_2~g \end{aligned} \right.\]

Équilibre de forces : \[\overrightarrow{T_2}=\overrightarrow{X_{12}}+\overrightarrow{T_3}\]

Relations du triangle : \[\frac{X_{12}}{\sin(\theta_2-\theta_1)}=\frac{T_2}{\sin(\pi/2+\theta_1)}=\frac{T_2}{\cos\theta_1}~~\Rightarrow~~X_{12}=m_2~g~(\theta_2-\theta_1)\]

b) Application du principe fondamental de la dynamique : \[\left\{ \begin{aligned} m_1~\frac{d^2x_1}{dt^2}&=X_1+X_{12}=-m_1~g~\theta_1+m_2~g~(\theta_2-\theta_1)\quad &&x_1=l_1~\theta_1\\ m_2~\frac{d^2x_2}{dt^2}&=X_2=-m_2~g~\theta_2 &&x_2=l_1~\theta_1+l_2~\theta_2 \end{aligned} \right.\]

En combinant ces relations, on obtient : \[\begin{aligned} m_1~l_1~\frac{d^2\theta_1}{dt^2}+(m_1+m_2)~g~\theta_1&=m_2~g~\theta_2 &&(1)\\ l_2~\frac{d^2\theta_2}{dt^2}+g~\theta_2=-l_1~\frac{d^2\theta_1}{dt^2}&=-\frac{1}{m_1}~\{m_2~g~\theta_2-(m_1+m_2)~g~\theta_1\}\quad &&(2)\\ l_2~\frac{d^2\theta_2}{dt^2}+g~\theta_2~\Big(1+\frac{m_1}{m_2}\Big)&=+\frac{1}{m_1}~(m_1+m_2)~g~\theta_1 &&(3) \end{aligned}\]

Et toutes simplifications faites : \[\left\{ \begin{aligned} \frac{d^2\theta_1}{dt^2}+\frac{m_1+m_2}{m_1}~\frac{g}{l_1}~\theta_1&=\frac{m_2}{m_1}~\frac{g}{l_1}~\theta_2\\ \frac{d^2\theta_2}{dt^2}+\frac{m_1+m_2}{m_1}~\frac{g}{l_2}~\theta_2&=\frac{m_1+m_2}{m_1}~\frac{g}{l_2}~\theta_1 \end{aligned} \right.\]

1.2. Exercice 2. Pendule conique

1.2.1. Énoncé

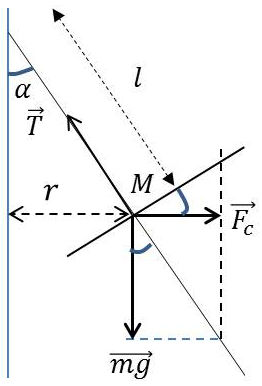Un système est constitué par une masse \(m\) de dimensions négligeables attachée à un fil de longueur \(l\) dont on peut négliger la masse. Ce dispositif est situé dans un champ de pesanteur d’accélération \(g\).

La masse \(m\), mise en mouvement, décrit un cercle situé dans un plan horizontal, le fil balayant un cône de révolution dont le demi-angle d’ouverture a pour valeur \(\alpha\).

Donner les valeurs de l’énergie cinétique \(E_c\), de l’énergie potentielle \(E_p\) et de la période de révolution \(T\) de ce système (l’origine de \(E_p\) étant prise pour \(\alpha=0\)).

1.2.2. Solution

1) Équilibre des forces

Trois forces s’équilibre en \(M\) :

– Force centrifuge \(\overrightarrow{Fc}\) : \[F_c=\frac{m~v^2}{r}\quad;\quad r=l\sin\alpha\]

– Pesanteur \(\overrightarrow{Z}\) : \[Z=m~g\]

– Tension du fil \(\overrightarrow{T}\) : \[\overrightarrow{T}+\overrightarrow{F_c}+\overrightarrow{Z}=\overrightarrow{0}\]

2) Projection sur la perpendiculaire à \(\overrightarrow{T}\) (élimination de la tension par projection) : \[mg~\sin\alpha=F_c~\cos\alpha=\frac{m~v^2}{l~\sin\alpha}\cos\alpha\]

On en déduit : \[F_c=m~g~\tan\alpha\quad;\quad v^2=g~l~\frac{\sin^2\alpha}{\cos\alpha}\]

– Énergie cinétique : \[\begin{aligned} &E_c=\frac{1}{2}~m~g~l~\frac{\sin^2\alpha}{\cos\alpha}\\ &\alpha=0\quad\Rightarrow\quad r=0\quad\Rightarrow\quad E_c=0 \end{aligned}\]

– Énergie potentielle :

Lorsque \(\alpha\) passe de la valeur \(0\) à sa valeur \(\alpha\), la masse s’élève de \(l~(1-\cos\alpha)\) : \[E_p=m~g~l~(1-\cos\alpha)\]

– Période de révolution \(T\) : \[T=\frac{2\pi~r}{v}=\dots=2\pi~\sqrt{\frac{l~\cos\alpha}{g}}\]

Remarquer que si l’on fait \(\alpha=0\), on retrouve la formule du pendule simple, le tour devenant un simple aller-retour : combinaison du mouvement pendulaire plan et d’une rotation.