1. Formule de Green-Riemann
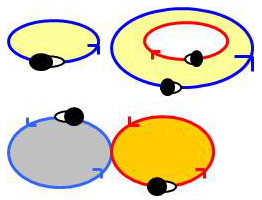On s’inspire de la règle du bonhomme d’Ampère traversé par l’axe \(Oz\). La formule ne s’applique que dans le plan (ici le plan \(xOy\)).
Dans ce repérage, l’orientation de la courbe frontière la gauche du bonhomme est dirigée vers l’intérieur du domaine.
On sait que la circulation le long d’une courbe est donnée par l’intégrale : \[I=\int_C\overrightarrow{V}\cdot\overrightarrow{dM}\quad;\quad~C=C1+C2\]
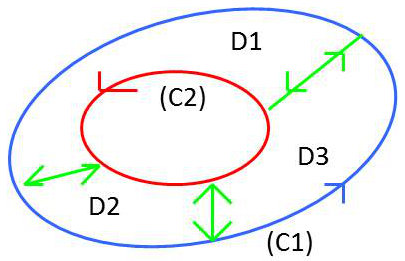On peut cependant introduire des domaines partiels, si besoin est, en fonction de la complexité.
Il faut orienter les frontières en considérant un double sens s’il y a recouvrement.
On pose : \[I_1=\int_{D1}\overrightarrow{V}\cdot\overrightarrow{dM}\qquad\text{etc.}\]
Puis, on fait la somme sur l’ensemble des domaines parcourus : \(I=I_1+I_2+\dots\)
1.1. Formule de Green-Riemann
Soient \(P(x,y)\) et \(Q(x,y)\) des fonctions continues sur un domaine \(D\) délimité par une frontière \(C\) (appelée souvent bord de \(D\)).
Si les dérivées \(P'_y\) et \(Q'_x\) existent et sont continues, alors on a (formule de Green-Riemann) : \[\int_C P~dx+Q~dy=\iint_D \Big(\frac{\partial Q}{\partial x}+\frac{\partial P}{\partial y}\Big)~dx~dy\]
Conséquences
Soit un domaine \(D\) et \(C\) le bord de \(D\).
Considérant respectivement les deux champs vectoriels définis par : \[P=0~;~Q =x\quad\rm{et}\quad P=y~;~Q=0\]
En leur appliquant la formule de Riemann, on obtient respectivement :
\[\begin{aligned} &\int_C x~dy=\iint_D dx~dy=~aire\\ &\int_C y~dx=\iint_D -~dx~dy=~-~aire\end{aligned}\]
On peut écrire par suite que : \[A=\frac{1}{2}~\int_C x~dy-y~dx\]
Cette nouvelle formule est intéressante pour calculer l’aire d’un secteur.
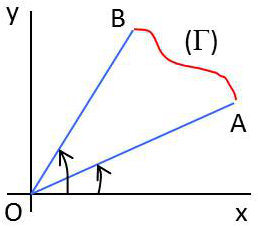Prenant l’équation de la droite \(OA\) (idem \(OB\)) : \[\frac{y}{x}=\frac{dy}{dx}\quad\Rightarrow\quad x~dy=y~dx\]
L’intégrale est alors nulle sur les circuits \(OA\) et \(OB\).
D’où l’expression de l’aire : \[A=\frac{1}{2}~\int_{\Gamma} (x~dy-y~dx)\]
En introduisant les coordonnées polaires : \[x=r~\cos\theta~~;~~y=r~\sin\theta\]
On obtient : \[A=\frac{1}{2}~\int_{\Gamma} r^2~d\theta\]
1.2. Théorème fondamental
Soient deux fonctions \(P(x,y)\) et \(Q(x,y)\) définies et continues sur un domaine \(D\) simplement connexe.
Soient \(P’_y\) et \(Q’_x\) leurs dérivées partielles également définies et continues sur ce domaine.
Pour que l’intégrale \(I\) soit nulle, \[I=\int_C P~dx+Q~dy\qquad~C\in D\]
il faut et il suffit que : \[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\]
Examinons les conséquences de ce théorème.
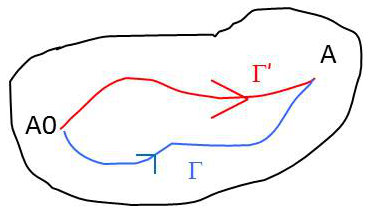Dans un domaine simplement connexe, deux chemins différents (\(\Gamma\) et \(\Gamma'\)) permettent de joindre les deux points \(A_0\) et \(A\).
On a donc : \[\int_{\Gamma+\Gamma'}P~dx+Q~dy=0\]
Par suite (tenant compte des signes) : \[J=\int_{A_0,\Gamma,A}P~dx+Q~dy=\int_{A,\Gamma',A_0}P~dx+Q~dy\]
Pour tout chemin allant de \(A_0\) à \(A\), l’intégrale curviligne \(J\) est la même. Donc si \(A_0\) est fixe et si \(A\) est mobile, l’intégrale \(J\) ne dépend que de la position de \(A\). C’est donc une fonction \(U(x,y)\).
On aura alors : \[dU=P~dx+Q~dy\]
Donc si l’on a : \[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\]
dans une région simplement connexe, \(P~dx+Q~dy\) est la différentielle d’une fonction \(U\) et réciproquement.
L’expression \((P~dx+Q~dy)\) est désignée sous le nom de forme de Pfaff.
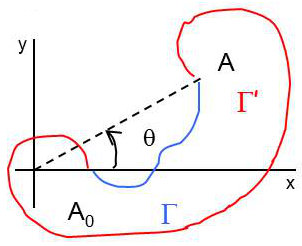Prenons à présent un contre-exemple. Considérons la fonction : \[U={\rm atan}\Big(\frac{y}{x}\Big)\]
L’origine est un point singulier appartenant au domaine.
Tous calculs faits, on a :
\[\begin{aligned} &P=\frac{\partial U}{\partial x}=-\frac{y}{x^2+y^2}\\ &Q=\frac{\partial U}{\partial y}=\frac{x}{x^2+y^2}\end{aligned}\]
Supposons maintenant que nous nous soyons donné \(P\) et \(Q\) en ignorant \(U\).
Existe-t-il une intégrale : \[I=\int_C P~dx+Q~dy\quad\text{avec}~C~\text{joignant}~A_0~\text{et}~A~?\]
Dans le plan : \[\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\]
Appliquons la formule de Green-Riemann en retirant le point \(O\) où \(P\) et \(Q\) ne sont pas définies : le domaine n’est plus simplement connexe. Les intégrales vont être différentes suivant le chemin choisi.
On aura donc :
\[\begin{aligned} &\int_{A_0,\Gamma,A}=U_A-U_{A_0}=I\\ &\int_{A_0,\Gamma',A}=U_A-U_{A_0}=I+2\pi\end{aligned}\]
1.3. Problème de flux
Prenons une surface doit être compacte, quarrable et orientable (ce qui n’est pas le cas de la surface de Moebius).
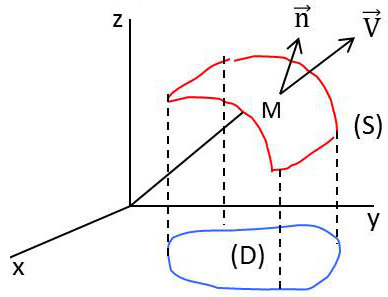On définit localement le flux par : \[\Phi=\iint\limits_S\overrightarrow{V}\cdot\overrightarrow{n}~ds\]
On pose : \[\overrightarrow{OM}=\overrightarrow{E}(u,v)\]
On a alors : \[\overrightarrow{n}=\frac{\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}}{|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|}\]
En reportant dans la formule du flux : \[\Phi=\iint\limits_S=\frac{(\overrightarrow{V},\overrightarrow{E'_u},\overrightarrow{E'_v})}{|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|}~ds\]
Dans le plan \([u,v]\) : \[\Phi=\iint\limits_S=\frac{(\overrightarrow{V},\overrightarrow{E'_u},\overrightarrow{E'_v})}{|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|}~|\overrightarrow{E'_u}\wedge\overrightarrow{E'_v}|~du~dv=\iint\limits_S(\overrightarrow{V},\overrightarrow{E'_u},\overrightarrow{E'_v})~du~dv\]
Pour fixer les idées, prenons le cas d’une surface \(z = f(x,y)\) \[\overrightarrow{P,Q,R}\quad;\quad\overrightarrow{E'_u}(1,0,p)\quad;\quad\overrightarrow{E'_v}(0,1,q)\]
Il vient alors : \[\Phi=\iint\limits_D(R-p~Q-q~P)~dx~dy\]
2. Formule de Green-Ostrogradsky
Soit un domaine \(D\) compact dont le bord est une surface \(S\). Supposons que sur \(D\) soit défini un champ de vecteurs continu à dérivées continues (champ régulier).
On démontre la formule de Green-Ostrogradsky : \[\iiint\limits_D {\rm div}\overrightarrow{V}~d\tau=\iint\limits_S\overrightarrow{V}\cdot\overrightarrow{n}~ds\]
La deuxième intégrale est l’expression du flux sortant du domaine par la surface enveloppante.
Lorsque le champ n’est pas régulier, la formule n’est plus applicable, ce que l’on peut voir avec le contre-exemple suivant :
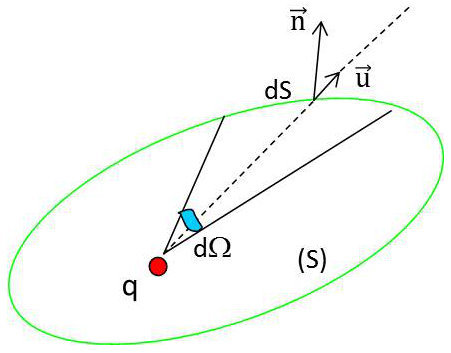
Le champ électrostatique d’une charge ponctuelle \(q\) est exprimé par, à une constante multiplicative près : \[\overrightarrow{E}=\frac{q}{r^2}~\overrightarrow{u}\]
Le flux sortant à travers l’élément de surface \(ds\) est donné par : \[d\Phi=\overrightarrow{E}\cdot\overrightarrow{n}~ds=\frac{q}{r^2}\overrightarrow{n}\cdot\overrightarrow{u}~ds\]
Soit encore : \[d\Phi=q~\frac{ds~\cos\alpha}{r^2}=q~d\Omega\]
\(\Omega\) représente l’angle solide entourant la charge (enveloppée par S).
On a donc : \[\iint\limits_S\overrightarrow{E}\cdot\overrightarrow{n}~ds=4\pi~q\]
Or, on sait que : \[{\rm div}\overrightarrow{E}=0\quad\Rightarrow\quad\iint\limits_R {\rm div}\overrightarrow{E}~d\tau=0\]
Il y a donc une contradiction.
On ne peut appliquer le théorème de Green-Ostrogradsky, car le champ n’est pas régulier en \(r\), donc pas défini en \(q\). Il faut en fait considérer le domaine comme amputé d’une sphère autour de \(q\). Alors seulement, le flux sera nul.
3. Formule de Stokes
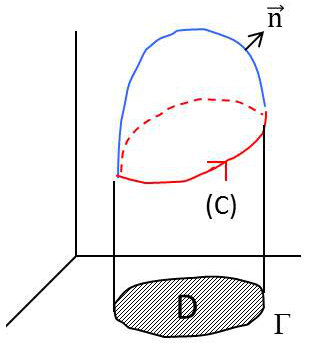On considère un domaine dans lequel est défini un champ vectoriel régulier et une courbe close de ce domaine.
On considère une surface s’appuyant sur \(C\).
La formule de Stokes est obtenue à partir de la transformation en intégrale de surface d’une intégrale curviligne : \[I=\int_C P~dx+Q~dy+R~dz\]
Cette surface étant exprimée par une fonction \(z=\varphi(x,y)\), on est ramené à un problème à deux variables.
L’application de la formule de Green-Riemann permet d’établir alors que : \[\int_C\overrightarrow{V}\cdot\overrightarrow{dl}=\iint\limits_S\overrightarrow{\rm rot}\overrightarrow{V}\cdot\overrightarrow{n}~ds\]
La circulation de \(\overrightarrow{V}\) le long d’une ligne \(C\) est égale au flux du rotationnel de \(\overrightarrow{V}\) à travers la surface \(S\) dont \(C\) est le support.
3.1. Théorème
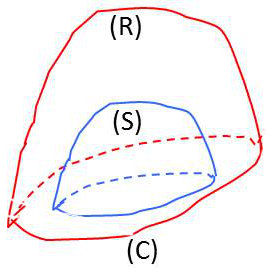Étant donnés une région compacte simplement connexe et un champ de vecteurs régulier sur cette région, la condition nécessaire et suffisante pour que ce champ de vecteurs soit un champ de gradients est que la circulation le long de toute courbe close de cette région soit nulle.
Soit une région simplement connexe \(R\). \[\overrightarrow{V}=\overrightarrow{\rm grad}\Phi\quad\Rightarrow\quad\overrightarrow{\rm rot}\overrightarrow{V}=\overrightarrow{0}\]
Et, d’après la formule de Stokes : \[\iint\limits_S\overrightarrow{\rm rot}\overrightarrow{V}\cdot\overrightarrow{n}~ds=\int_C\overrightarrow{V}\cdot\overrightarrow{dl}=0\]
4. Intégration de forme différentielle à trois dimensions
Supposons une région \(R\) compacte simplement connexe et un champ régulier : \[\overrightarrow{V}=\{P(x,y,z);~Q(x,y,z);~R(x,y,z)\}\]
Alors : \[\overrightarrow{V}=\overrightarrow{\rm grad}(f)\quad\text{si et seulement si}\quad\overrightarrow{\rm rot}\overrightarrow{V}=\overrightarrow{0}\]
C’est à dire que :
Il existe alors une fonction \(f\) telle que : \[df=\frac{\partial f}{\partial x}~dx+\frac{\partial f}{\partial y}~dy+\frac{\partial f}{\partial z}~dz=P~dx+Q~dy+R~dz\]
Ainsi, la condition nécessaire et suffisante pour que \(P~dx+Q~dy+R~dz\) soit intégrable (différentielle d’une fonction \(f\)) est que l’on ait, dans la région considérée : \[\frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}\quad;\quad\frac{\partial R}{\partial x}=\frac{\partial P}{\partial z}\quad;\quad\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}\]
Un cas particulier est la formule de Green-Riemann (espace à deux dimensions)
