1. Introduction

En raison de l’uniformité du temps, de l’homogénéité de l’espace et de l’isotropie de l’espace, nous devons trouver trois lois de conservation :

• Conservation de l’énergie mécanique

• Conservation de l’impulsion

• Conservation du moment cinétique

2. Conservation de l’énergie mécanique

La conservation de l’énergie mécanique provient de l’uniformité du temps. Quand un système est en mouvement, \((q^i,~\dot{q_i})\) varient dans le temps, mais il se peut que certaines fonctions \(f(q^i,~\dot{q_i})\) soient des intégrales premières des équations de Lagrange.

Considérons un système isolé (ou fermé). Comme \(t\) est uniforme, le lagrangien ne doit pas dépendre explicitement du temps \(L(q^i,\dot{q_i})\) : \[\frac{dL}{dt}= \frac{\partial L}{\partial q^i}~\frac{dq^i}{dt}+\frac{\partial L}{\partial\dot{q}^i}~\frac{d\dot{q}^i}{dt}= \frac{\partial L}{\partial q^i}~\dot{q}^i+\frac{\partial L}{\partial\dot{q}^i}~\ddot{q}^i\]

Mais on a : \[\frac{d}{dt}\Big(\frac{\partial L}{\partial\dot{q}^i}\Big)-\frac{\partial L}{\partial q^i}=0\]

Il vient donc : \[\frac{dL}{dt}= \frac{d}{dt}\Big(\frac{\partial L}{\partial\dot{q}^i}\Big)~\dot{q}^i +\Big(\frac{\partial L}{\partial\dot{q}^i}\Big)~\frac{d\dot{q}^i}{dt}= \frac{d}{dt}\Big(\frac{\partial L}{\partial\dot{q}^i}~\dot{q}^i\Big)\]

On a donc : \[\frac{d}{dt}\Big(\dot{q}^i~\frac{\partial L}{\partial\dot{q}^i}-L\Big)=0\quad\Rightarrow\quad \dot{q}^i~\frac{\partial L}{\partial\dot{q}^i}-L=E=cte\]

Dans cette intégrale première, la constante \(E\) est l’énergie mécanique du système. \[L=T(q^i,~\dot{q}^i)-U(q^i)\quad\Rightarrow\quad\frac{\partial L}{\partial\dot{q}^i}=\frac{\partial T}{\partial\dot{q}^i}\]

On a donc : \[E=\dot{q}^i~\frac{\partial L}{\partial\dot{q}^i}-L(q^i)\]

Par ailleurs : \[T=\sum a_{ik}~(q^i)~\dot{q}^i~\dot{q}^k \qquad\text{et}\qquad 2~T=\dot{q}^i~\frac{\partial T}{\partial q^i}\]

On a simultanément : \[E=2~T-U\qquad\text{et}\qquad L=T-U\]

Par suite : \[E=T+U\]

3. Conservation de l’impulsion

La conservation de l’impulsion provient de l’homogénéité de l’espace. On considère toujours un système fermé et ses propriétés ne changent pas quand il est soumis à un déplacement parallèle en bloc : \[\overrightarrow{r_a}\quad\rightarrow\quad\overrightarrow{r_a}+\overrightarrow{\varepsilon}\]

\(L\) doit être invariant dans cette transformation et on postule que \(L(\overrightarrow{r_a},~\overrightarrow{v_a})\) : \[\delta L=\frac{\partial L}{\delta\overrightarrow{r_a}}\cdot\delta\overrightarrow{r_a}+\frac{\partial L}{\delta\overrightarrow{v_a}}\cdot\delta\overrightarrow{v_a}\]

Mais les vitesses ne varient pas et, en adoptant la notation \(\delta\overrightarrow{r_a}=\overrightarrow{\varepsilon}\) : \[\delta L=\overrightarrow{\varepsilon}\cdot\sum_a\frac{\partial L}{\delta\overrightarrow{r_a}}=0 \qquad\text{avec}\quad\overrightarrow{\varepsilon}\neq\overrightarrow{0}\]

Comme : \[\frac{d}{dt}\Big(\frac{\partial L}{\partial\overrightarrow{v_a}}\Big)-\frac{\partial L}{\partial\overrightarrow{r_a}}=\overrightarrow{0}\]

Il vient : \[\frac{d}{dt}\sum_a\frac{\partial L}{\partial\overrightarrow{v_a}}=\overrightarrow{0}\]

Par suite : \[P=\sum_a\frac{\partial L}{\partial\overrightarrow{v_a}}=\overrightarrow{cte}\]

Dans un système de points matériels : \[L=\sum_a\frac{m_a~\overrightarrow{v_a}^2}{2}-U(\overrightarrow{r_a})\]

Par suite : \[\frac{\partial L}{\partial\overrightarrow{v_a}}=m_a\overrightarrow{v_a}\qquad;\qquad \overrightarrow{P}=\sum_a m_a~\overrightarrow{v_a}\]

3.1. Remarque 1

De ce qui précède, on peut écrire :

\[\begin{aligned} &\sum_a\frac{\partial L}{\partial\overrightarrow{r_a}}=\frac{d}{dt}\sum_a\frac{\partial L}{\partial\overrightarrow{v_a}}\\ &\sum_a-\frac{\partial U}{\partial\overrightarrow{r_a}}=\frac{d}{dt}\sum_a\frac{\partial L}{\partial\overrightarrow{v_a}}=\sum_a\overrightarrow{F_a}=\overrightarrow{0}\end{aligned}\]

On retrouve le principe d’action et de réaction.

3.2. Remarque 2

Reprenons la formule : \[\frac{d}{dt}\Big(\frac{\partial L}{\partial\dot{q}^i}\Big)-\frac{\partial L}{\partial q^i}=0\]

Introduisons l’impulsion généralisée : \[p_i=\frac{\partial L}{\partial\dot{q}^i}\]

On voit que si : \[L=\sum_a\frac{m_a~\overrightarrow{v_a}^2}{2}-U(\overrightarrow{r_a})\]

on retrouve bien :

\[\begin{aligned} \frac{\partial L}{\partial\overrightarrow{v_a}}&=m_a~\overrightarrow{v_a}\\ \frac{\partial L}{\partial\dot{q}^i}&=-\frac{\partial U}{\partial q^i}=F_i &&\text{force généralisée}\\ \frac{dP_i}{dt}&=F_i &&\text{principe fondamental de la dynamique généralisé}\end{aligned}\]

3.3. Remarque 3

Reprenons la relation : \[\overrightarrow{P_a}=\sum_a m_a~\overrightarrow{v_a}\]

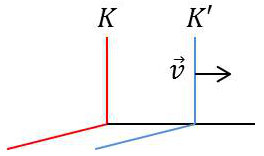
Si l’on change de repère galiléen : \[\overrightarrow{v_a}=\overrightarrow{v'_a}+\overrightarrow{v}\]

Il vient : \[\overrightarrow{P_a}=\sum_a m_a~\overrightarrow{v_a}= \sum_a m_a~\overrightarrow{v'_a}+\sum_a m_a~\overrightarrow{v}= \overrightarrow{P'}+m~\overrightarrow{v}\]

Il existe un point \(K'\) tel que : \[\overrightarrow{P'}=0\qquad\Rightarrow\qquad\overrightarrow{P}=m~\overrightarrow{v}\]

Alors : \[\overrightarrow{v}=\frac{\overrightarrow{P}}{m}=\frac{\sum_a m_a~\overrightarrow{v_a}}{\sum_a\overrightarrow{v_a}}\]

Et en intégrant par rapport à \(\overrightarrow{v}\) : \[\overrightarrow{R}=\frac{\sum_a m_a~\overrightarrow{r_a}}{\sum_a\overrightarrow{v_a}}\]

\(R\) caractérise le centre de gravité du système par rapport à \(K\) (dans un système isolé, \(G\) ne bouge pas).

Si le système n’est pas isolé \((\overrightarrow{P}\neq\overrightarrow{cte})\) : \[\frac{\overrightarrow{dP}}{dt}=\sum m_a~\frac{d\overrightarrow{v_a}}{dt}= \sum m_a~\overrightarrow{\gamma_a}=\sum\overrightarrow{F_i}+\sum\overrightarrow{F_e}=\sum\overrightarrow{F_e}\]

On retrouve le théorème du centre de gravité : \[\frac{\overrightarrow{dP}}{dt}=\frac{d}{dt}(m~\overrightarrow{v})=\sum\overrightarrow{F_e}\]

4. Conservation du moment cinétique

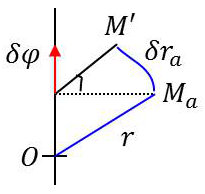Le principe de conservation du moment cinétique résulte de l’isotropie de l’espace. Pour un système fermé, une rotation d’ensemble ne change rien aux lois de la mécanique. \[\overrightarrow{\delta r_a}=\overrightarrow{\delta\varphi}\wedge\overrightarrow{r_a}\]

Écrivons que \(L\) n’est pas modifié dans cette rotation infinitésimale : \[q^i~\rightarrow~r_a\quad;\quad \dot{q}^i~\rightarrow~v_a\quad;\quad L(r_a,~v_a)\]

On a : \[\delta L=\frac{\partial L}{\partial\overrightarrow{v_a}}\cdot\overrightarrow{\delta v_a}+\delta L= \frac{\partial L}{\partial\overrightarrow{r_a}}\cdot\overrightarrow{\delta r_a}\]

Par ailleurs : \[\frac{d}{dt}\Big(\frac{\partial L}{\partial\overrightarrow{v_a}}\Big)-\frac{\partial L}{\partial\overrightarrow{r_a}}=\overrightarrow{0}\]

D’où : \[\frac{\partial L}{\partial\overrightarrow{v_a}}\cdot\overrightarrow{\delta v_a}+\frac{d}{dt}\Big(\frac{\partial L}{\partial\overrightarrow{v_a}}\Big)\cdot\overrightarrow{\delta r_a}=0\]

Par ailleurs :

\[\begin{aligned} &\overrightarrow{P_a}=\frac{\partial L}{\partial\overrightarrow{v_a}}\\ &\sum\overrightarrow{P_a}\cdot(\overrightarrow{\delta\varphi}\wedge\overrightarrow{v_a})+ \sum\overrightarrow{\dot{P_a}}\cdot(\overrightarrow{\delta\varphi}\wedge\overrightarrow{r_a})=0\\ &\overrightarrow{\delta\varphi}\cdot\sum(\overrightarrow{v_a}\wedge\overrightarrow{P_a})+ \overrightarrow{\delta\varphi}\cdot\sum(\overrightarrow{r_a}\wedge\overrightarrow{\dot{P_a}})=0\qquad\forall~\overrightarrow{\delta\varphi}\end{aligned}\]

On a donc : \[(\overrightarrow{v_a}\wedge\overrightarrow{P_a})+(\overrightarrow{r_a}\wedge\overrightarrow{\dot{P_a}})=\overrightarrow{0}\]

C’est-à-dire : \[\overrightarrow{\dot{r_a}}\wedge\overrightarrow{P_a}+\overrightarrow{r_a}\wedge\overrightarrow{\dot{P_a}}=\overrightarrow{0}\]

Ou encore : \[\frac{d}{dt}(\overrightarrow{r_a}\wedge\overrightarrow{P_a})=\overrightarrow{0}\]

Et on a donc : \[\sum_a(\overrightarrow{r_a}\wedge\overrightarrow{P_a})=\overrightarrow{M}=\overrightarrow{cte}\]