1. Introduction

À la notion d’événement \(E_i\), on associe un ensemble \(E_i\). Sur cet ensemble, on définit une mesure qui sera la probabilité \(p_i\). On définit un ensemble noté \(\Omega\) formé de tous les événements élémentaires notés \(\omega\). Cet ensemble est dit complet, tous les événements élémentaires possibles étant présents, condition indispensable pour pouvoir effectuer un calcul de probabilités. Un événement \(A\) (non élémentaire) sera un sous-ensemble de \(\Omega\). On écrira alors : \(A\subset \Omega\).

Prenons l’exemple du lancer d’un dé :

• \(\Omega=\{1,2,3,4,5,6\}\) est l’ensemble (complet) des événements élémentaires.

• \(A=\{2,4,6\}\) est le sous-ensemble des nombres pairs.

• Le tirage de \(\omega =3\) représente un événement élémentaire.

• Le tirage de \(\omega~pair\) représente un événement.

2. Correspondance événement – ensemble

Soit \(\omega\in\Omega\), un événement élémentaire et deux événements \(A\subset\Omega\) et \(B\subset\Omega\).

D’un point de vue axiomatique, on peut écrire :

\[\begin{aligned} &\quad \textit{Évènements} &&\quad \textit{Ensembles} \\ \hline &\text{$A$ réalisé} &&\omega \in A\\ &\text{$A$ ou $B$ réalisé} &&\omega \in A\cup B \\ &\text{$A$ et $B$ réalisés} &&\omega \in A\cap B \\ &\text{$A$ réalisé implique $B$ réalisé} &&\forall\omega\in A \quad \omega\in B &&\Rightarrow \quad A\subset B \\ &\text{$A$ impossible} &&A=\varnothing \\ &\text{Événements complémentaires } &&A,~\bar{A}=C_{\Omega}(A) &&\Rightarrow \quad A \cup \bar{A}=\Omega \\ &\text{Événements incompatibles} &&A\cap B=\varnothing\end{aligned}\]

3. Probabilité et mesure

3.1. Notion de mesure

À chaque sous-ensemble \(X\subset E\), on peut associer un nombre \(m(X)\) non négatif ayant les propriétés suivantes :

• \(m(E)\) est fini

• \(X_1,~X_2,~\dots,~X_N\) étant des sous-ensembles de \(E\) en nombre fini ou dénombrable,

\[m(X)\leq m(X_1)+m(X_2)+\dots~\quad \text{où} \quad X=X_1\cup X_2\cup~\dots\]

Si les sous-ensembles sont disjoints deux à deux, l’inégalité devient une égalité.

On dit que \(m(X)\) est une mesure sur \(E\).

\[\begin{aligned} &\text{Pour deux sous-ensembles disjoints :} && m(X_1\cup X_2)=m(X_1)+m(X_2) \\ &\text{Pour deux sous-ensembles non disjoints :} && m(X_1\cup X_2)=m(X_1)+m(X_2)-m(X_1\cap X_2) \\ &\text{S'il y a inclusion :} && X_1\subset X_2 \ \ ; \ \ m(X_1)<m(X_2)\end{aligned}\]

3.2. Notion de probabilité

On peut comprendre intuitivement que l’on puisse prolonger la notion de mesure et l’étendre à celle de probabilité. Nous prendrons deux exemples pour fixer les idées, le premier dans le cadre de probabilités discrètes, le second dans le cadre de probabilités continues.

Exemple 1 : probabilités discrètes

Quelle est la probabilité de tirer un nombre pair dans un jet de dé ?

\[\begin{aligned} &\Omega=\{1,2,3,4,5,6\} && m(\Omega)=card(\Omega)=6 && \text{Nombre total de cas} \\ &A=\{2,4,6\} && m(A)=card(A)=3 && \text{Nombre de cas favorables}\end{aligned}\]

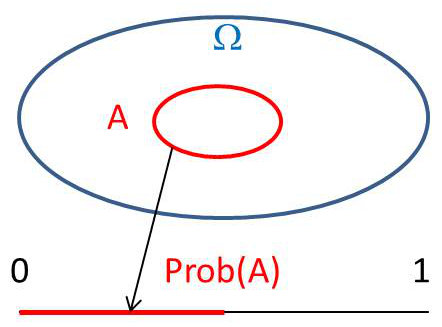On a donc : \[prob(A)=\frac{m(A)}{m(\Omega)}=\frac{1}{2}\]

La mesure présente un caractère de dénombrement.

Exemple 2 : probabilités continues

On jette une pièce sur un ensemble formé de deux disques concentriques de rayons \(r<R\). Quelle est la probabilité pour que la pièce tombe sur le disque plus central ?

Réponse : \[prob(A)=\frac{m(A)}{m(\Omega)}=\frac{S_A}{S_{\Omega}}=\left(\frac{r}{R}\right)^2\]

La mesure présente un caractère (continu) de surface.

Désignons par \(F=P(\Omega)\) l’ensemble des parties de \(\Omega\). À chaque ensemble \(A\) (événement) de \(F=P(\Omega)\), on fait correspondre le nombre \(p(A)\). On définit ainsi une application de l’ensemble \(p(\Omega)\) dans l’ensemble \(\mathbb{R}\) des nombres réels.

Le triplet \(\{\Omega,F,p\}\) est appelé espace probabilisé. On dit que \(p(A)\) est la probabilité pour que l’événement \(A\) se réalise.

4. Axiomes de Kolmogoroff

Rappelons deux formules (conjointes) d’axiomatique :

\[\left\{ \begin{aligned} p(X_1\cup X_2)=p(X_1)+p(X_2)-p(X_1\cap X_2)\\ p(X_1\cap X_2)=p(X_1)+p(X_2)-p(X_1\cup X_2) \end{aligned} \right.\]

On appelle mesure de probabilité sur un ensemble \(\Omega\) (appelé parfois Univers) toute application \(p(\Omega)\rightarrow \mathbb{R}\) satisfaisant aux trois conditions suivantes :

\[\left\{ \begin{aligned} &\forall X\subset \Omega && 1<p(X)\leq 0 \\ & && p(\Omega)=1 \\ &X\cap Y=\varnothing \quad \Rightarrow ~ && p(X\cup Y)=p(X)+p(Y) \end{aligned} \right.\]

Plus généralement, pour des ensembles disjoints deux à deux : \[p(X_1\cup X_2\cup ..... )=\sum_{i=1}^{+\infty}p(X_i)\]

Autres propriétés :

\[\begin{aligned} & \text{Événement impossible :} && p(\varnothing)=0 \\ & \text{Inclusion :} && X\subset Y \Rightarrow p(X)\leq p(Y)\end{aligned}\]

En considérant des événements complémentaires \(X\) et \(\bar{X}=C_{\Omega}(X)\), on obtient une formule très simple, mais en fait très utile dans certains problèmes de probabilités. Cette formule est dite axiome des probabilités contraires : \[p(X)+p(\bar{X})=1 \quad \text{ou} \quad p(\bar{X})=1-p(X)\]

5. Trois théorèmes fondamentaux

Trois théorèmes fondamentaux sont relatifs aux probabilités conditionnelles, à la notion d’indépendance des événements et à la règle de Bayes sur les hypothèses a priori.

5.1. Probabilités conditionnelles

On considère deux événements \(A\) et \(B\). Quelle est la probabilité pour que \(B\) se réalise alors que \(A\) s’est déjà réalisé ? \[p(B/A)=\frac{p(B\cap A)}{p(A)}\]

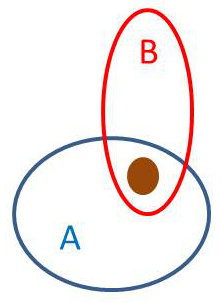Nous démontrerons cette proposition dans le cas d’une distribution discrète de probabilité en admettant, sans perte de rigueur, sa généralisation au cas d’une distribution continue.

\[\begin{aligned} p(A)&=\frac{card(A)}{card(\Omega)}\\ p(B/A)&=\frac{card(B\cap A)}{card(A)}\end{aligned}\]

On peut dire que la réalisation de \(A\) sert de référence à celle de \(B\) (plus exactement \(B\cap A\)). Ce que l’on peut percevoir intuitivement sur le dessin.

On peut écrire : \[\frac{card(B\cap A)}{card(A)}=\frac{card(B\cap A)}{card(\Omega)}\cdot\frac{card(\Omega)}{card(A)} \qquad c.q.f.d.\]

La formule établie est en général utilisée d’une autre manière : \[p(B\cap A)=p(B/A)~p(A)\]

Exemple

Une urne contient \(3\) boules blanches et \(5\) boules noires, identiques au toucher. En tirant deux boules au hasard (et sans remise). Quelle est la probabilité pour que l’on tire deux boules blanches ?

• Événement A : première boule blanche (sur un total de \(8\) boules)

• Événement B : deuxième boule blanche (sur un total de \(8-1=7\) boules)

\[p(A)=3/8 \quad ; \quad p(B/A)=2/7\] \[p(B\cap A)=p(B/A)~p(A)= \frac{3}{8}\times \frac{2}{7}=\frac{3}{28}\]

5.2. Indépendance

Il y a indépendance si la réalisation de \(A\) est sans influence sur celle de \(B\). On a alors : \[p(B/A)=p(B) \quad \Rightarrow \quad p(B\cap A)=p(B)~p(A)\]

Reprenant l’exemple précédent et supposant que l’on ait remis la boule dans l’urne après la première phase, on aurait obtenu le résultat différent suivant : \[p(B\cap A)=p(B)~p(A)=\frac{3}{8}\times \frac{3}{8}=\frac{9}{64}\]

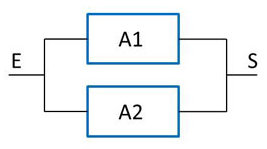Exemple Le système ci-contre fonctionne correctement si les deux appareils fonctionnent correctement. Les probabilités de panne sont respectivement de \(0,8\) et de \(0,7\). La probabilité pour que le système tombe en panne est donc \(p=0.8\times 0.7=0.56\).

5.3. Règle des hypothèses ou règle de Bayes

On considère un ensemble complet d’hypothèses indépendantes \(\{H_1,\) \(H_2,\) \(\dots,\) \(H_n\}\). Cherchons à déterminer laquelle de ces hypothèses a priori peut apparaître comme la plus vraisemblable.

Avant l’expérience, les probabilités de ces hypothèses sont données : \(\big\{p(H_1),~p(H_2),~\dots,~p(H_n)\big\} \)

L’expérience a réalisé un certain événement \(E\). Une hypothèse \(H_i\) a été émise sur cette réalisation de \(E\). Quelle est la validité \(p(H_i/E)\)de cette hypothèse ?

D’après le théorème des probabilités conditionnelles :

\[\begin{aligned} p(E\cap H_i)&=p(E)~p(H_i/E)=p(H_i)~p(E/H_i) \qquad i=1,~2,~3,~\dots,~n\\ p(H_i/E)&=\frac{p(H_i)~p(E/H_i)}{p(E)}\end{aligned}\]

L’événement est réalisé avec l’une des hypothèses (indépendantes) : \[E=(H_1\cap E)\cup \dots\cup (H_n\cap E)\]

D’où : \[p(E)=\sum_{i=1}^{i=n}p(H_i/E)=\sum_{i=1}^{i=n}p(H_i)~p(E/H_i)\]

Par suite : \[p(H_i/E)=\frac{p(H_i)~p(E/H_i)}{\sum_{i=1}^{i=n}p(H_i)~p(E/H_i)}\]

Exemple

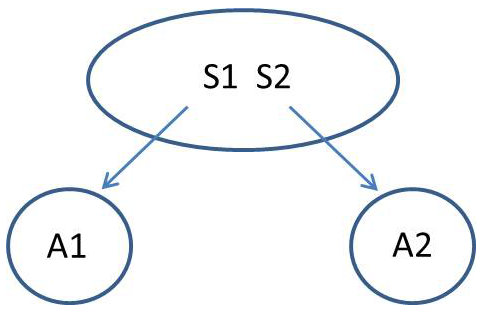Un système \(S\) est susceptible de se trouver dans l’un des deux états \(S_1\) ou \(S_2\). Des observations ont montré que le système se trouve dans l’état \(S_1\) environ \(30~\%\) du temps, donc dans l’état \(S_2\) environ \(70~\%\) du temps. Le système est en relation avec deux stations \(A_1\) et \(A_2\).

La station \(A_1\) annonce un état \(S_1\), mais on sait qu’elle fournit des données erronées dans \(2~\%\) des cas. La station \(A_2\) annonce un état \(S_2\), mais on sait qu’elle fournit des données erronées dans \(8~\%\) des cas.

À un certain moment, la station \(A_1\) indique que le système est dans l’état \(S_1\) alors que la station \(A_2\) annonce que le système est dans l’état \(S_2\). Laquelle de ces deux communications est la plus vraisemblable ?

Hypothèses a priori :

• Le système est dans l’état \(S_1\) [\(p(H_1)=0.3\)]

• Le système est dans l’état \(S_2\) [\(p(H_2)=0.7\)]

Événement \(E\) :

• \(A_1\) annonce \(S_1\)

• \(A_2\) annonce \(S_2\)

 
Première possibilité
Information \(A_1\) vraie (\(p_1=0.98)\) et information \(A_2\) fausse (\(p_2=0.08\)) \[p(E/H_1)=0.98\times 0.08=0.074\] Deuxième possibilité
Information \(A_1\) fausse (\(p_1=0.02)\) et information \(A_2\) vraie (\(p_2=0.92\)) \[p(E/H_2)=0.02\times 0.92=0.0184\]

On applique la formule de Bayes :

\[\begin{aligned} p(H_1/E)&=\frac{p(H_1)~p(E/H_1)}{p(H_1)~p(E/H_1)+p(H_2)~p(E/H_2)}\\ &=\frac{0.3\times 0.0784}{(0.3\times 0.0784)(0.7\times 0.0184)}=0.6462\end{aligned}\]

On en conclut que l’information en provenance de la station \(A_1\) est la plus vraisemblable.