1. Fonction de répartition. Densité de probabilité
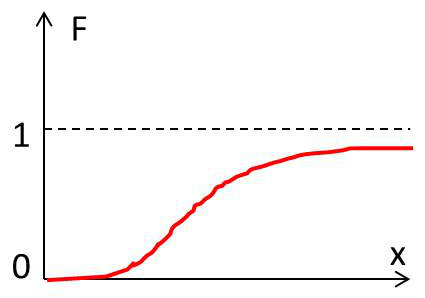La forme de la fonction de répartition se déduit intuitivement de la forme associée à une variable discrète (forme en marche d’escalier de l’épreuve du lancer de dé).
En transposant, tout au moins dans les premières définitions, ce qui a été vu dans le cas de la variable discrète, on commencera par rappeler que : \[Pr(x\leq X<x+\Delta x)=F(x+\Delta x)-F(x)\]
En faisant tendre \(\Delta x\) vers 0, on voit que : \[lim_{\Delta x\rightarrow 0}\frac{Pr(x\leq X<x+\Delta x)}{\Delta x} =lim_{\Delta x\rightarrow 0}\frac{F(x+\Delta x)-F(x)}{\Delta x}=F'(x)\]
On posera : \[f(x)=lim_{\Delta x\rightarrow 0}\frac{F(x+\Delta x)-F(x)}{\Delta x}=F'(x)\]
Cette nouvelle fonction apparaît alors comme une probabilité moyenne par unité de longueur de l’intervalle. Il s’agit donc d’une densité : on l’appellera densité de probabilité. On peut alors écrire : \[F(x)=\int_{-\infty}^x dF(u) \qquad \text{avec} \quad dF(u)=f(u)~du\]
On remarquera, à titre de contrôle, que : \[F(x)=\int_{-\infty}^x dF(u)=F(x)-F(-\infty)=F(x)-0=F(x)\]
2. Notion de probabilité pour une variable continue
Reprenons la relation générale : \[Pr(x\leq X<\beta)=F(\beta)-F(x)\]
Faisons tendre \(\beta\) vers \(x\). Il vient : \[Pr(X=x)=lim_{\beta\rightarrow x}\big\{F(\beta)-F(x)\big\}\]
Si \(F\) était discontinue, on devrait dire que la limite est égale à la valeur du saut de la fonction en ce point.Dans la mesure où F est continue, le cas de notre étude, cette limite est égale à \(0\).
Nous dirons que des variables aléatoires sont continues seulement si leurs fonctions de répartition le sont partout. La probabilité d’une valeur quelconque d’une variable continue est égale à zéro. On devra raisonner sur des intervalles et écrire alors : \[f(x)~dx=Pr(x<X<x+dx)\]
On peut d’abord vérifier que : \[\int_{-\infty}^{+\infty}f(x)~dx=1\]
Cette intégrale correspond à une normalisation de la densité de probabilité \(f(x)\). Dans tout problème de probabilités appliqué aux variables continues, il convient de s’assurer toujours du respect de cette condition. Elle sera particulièrement présente lorsqu’il s’agira de travailler sur un changement de variable.
On notera également que : \[Pr(x<X<\beta)=\int_x^{\beta}f(u)~du=F(\beta)-F(x)\]
Application :
Soit une variable aléatoire \(X\) définie par la densité de probabilité :
\[\begin{aligned} f(x)&=a\cos x && -\pi/2\leq x<+\pi/2\\ f(x)&=0 && x<-\pi/2 \quad\text{ ou }\quad x>+\pi/2\end{aligned}\]
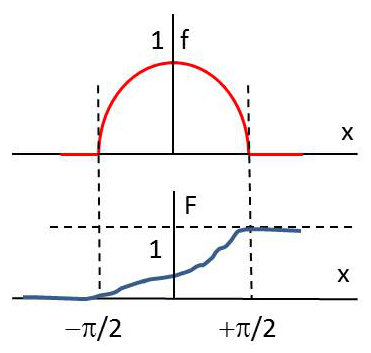Il faut tout d’abord appliquer le critère de normalisation pour déterminer la valeur de \(a\): \[\int_{-\infty}^{+\infty}f(x)~dx=1 ~\text{ c.à.d. : } \int_{-\pi/2}^{+\pi/2}a\cos x~dx=1 ~~\Rightarrow~~ a=1/2\]
Passons ensuite à la fonction de répartition : \[x<\pi/2~: \quad f(x)~dx=dF(x)=0 ~~\Rightarrow~~ F(x)=cte\]
Par continuité à la limite \((-\infty)\), il vient \(F(x)=0\).
De même (valeurs extrêmes supérieures) : \[x > \pi/2~: \quad f(x)dx=dF(x)=0 ~~\Rightarrow~~ F(x)=cte\]
Par continuité à la limite \((+\infty)\), il vient \(F(x)=1\).
On a donc pour \(-\pi/2\leq x\leq +\pi/2\) : \[F(x)=\int_{-\pi/2}^x\frac{1}{2}\cos u~du=\frac{1}{2}(\sin x+1)\]
On pourra calculer ensuite, à titre d’exemple : \[Pr\big(x\in \big[0,\frac{\pi}{4}\big]\big)=Pr\big(0\leq X\leq \frac{\pi}{4}\big)=F\big(\frac{\pi}{4}\big)-F(0)=\frac{\sqrt{2}}{4}\]
