1. Définitions

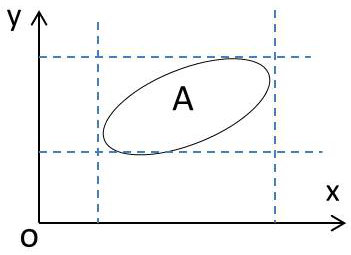Un couple de variables aléatoires continues \((X,Y)\) est défini par sa densité de probabilité \(f(x,y)\). Cette densité doit respecter la condition de normalisation, c’est-à-dire que, intégrée à tout l’espace de probabilité, on doit avoir : \[\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)~dx~dy=1\]

L’expression de la probabilité est classique : \[Pr\big\{(x,y)\in A\big\}=\int\int_Af(x,y)~dx~dy\]

2. Probabilités marginales

Par analogie avec le cas des variables discrètes,on peut définir des variables marginales, les probabilités associées ainsi que les espérances mathématiques et les moments.

\[\begin{aligned} f_x(x)=\int_{-\infty}^{+\infty}f(x,y)~dx~dy \qquad x \text{ fixé} \\ f_y(y)=\int_{-\infty}^{+\infty}f(x,y)~dx~dy \qquad y \text{ fixé}\end{aligned}\]

D’où les valeurs moyennes marginales :

\[\begin{aligned} E(X)=\int_{-\infty}^{+\infty}x~f_x(x)~dx=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}x~f(x,y)~dx~dy\\ E(Y)=\int_{-\infty}^{+\infty}y~f_y(y)~dy=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}y~f(x,y)~dx~dy\end{aligned}\]

3. Probabilités conditionnelles

On part de la formule générale : \[Pr(B/A)=\frac{Pr(B\cap A)}{Pr(A)}\]

En se situant toujours sur un intervalle \((dx,dy)\), cela reviendra à écrire : \[Pr(y<Y<y+dy~/~x<X<x+dx)=\frac{Pr(y<Y<y+dy,~x<X<x+dx)}{Pr(x<X<x+dx)}\]

En faisant tendre \(dx\rightarrow 0\), le premier membre peut s’écrire : \[Pr(y<Y<y+dy~/~X=x)=f(y/x)~dx\]

On reconnaît l’expression de la densité de probabilité conditionnelle de \(y\), \(x\) étant réalisée.

On peut alors écrire : \[\frac{Pr(y<Y<y+dy,~x<X<x+dx)}{Pr(x<X<x+dx)}=\frac{f(x,y)~dx~dy}{f_x(x)~dx}=\frac{f(x,y)~dy}{f_x(x)}\]

En définitive, les expressions respectives des densités de probabilité marginales seront : \[f(y/x)=\frac{f(x,y)}{f_x(x)} \quad ; \quad f(x/y)=\frac{f(x,y)}{f_y(y)}\]

4. Variables indépendantes

Dans ce cas, la réalisation de \(X\) n’a aucune influence sur la réalisation de \(Y\). On obtient un résultat analogue à celui du cas discret : \[f(y/x)=f_y(y) \ \ \ \rightarrow f(x,y)=f_x(x)~f_y(y)\]

5. Fonction de répartition

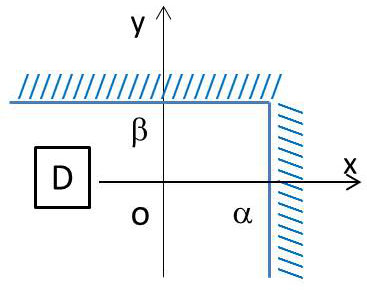Le raisonnement est celui de la simple extension du cas discret, le déplacement du point courant \(P\) ne s’effectuant plus sur une droite mais sur une surface : \[F(\alpha,\beta)=Pr(X<\alpha,~Y<\beta)=Pr(X,Y)\in (D)\]

avec le respect des conditions suivantes :

\[\begin{aligned} &F(X,Y)>0 \\ &F(+\infty,+\infty)=1 && (X,Y) \text{ est sûrement quelque part} \\ &F(-\infty,y)=0 && X \text{ ne peut être inférieur à } -\infty\\ &F(x,-\infty)=0 && Y \text{ ne peut être inférieur à } -\infty\end{aligned}\]

6. Relations avec la densité de probabilité

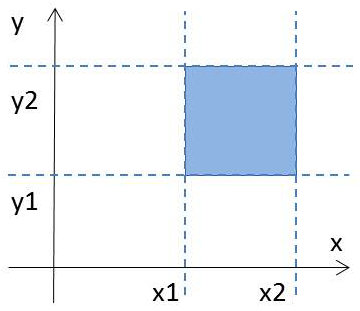Le calcul de la probabilité revient toujours à un calcul sur la fonction de répartition. Le recours à la représentation par une surface permet de mieux comprendre la formulation (additions et soustractions de surface) : \[Pr\{(X,Y)\in D\}=F(x_2,y_2)+F(x_1,y_1)-F(x_1,y_2)-F(x_2,y_1)\]

Posons : \[x_2-x_1=\Delta x \quad ; \quad y_2-y_1=\Delta y\]

Et adoptons, pour la commodité des calculs, la convention suivante : \[x_1 \rightarrow x \quad \text{et} \quad y_1 \rightarrow y\]

On a alors : \[Pr\{(X,Y)\in D\}=F(x+\Delta x,~y+\Delta y)-F(x,~y+\Delta y)-F(x+\Delta x,~y)+F(x,y)\]

Divisons les deux membres de cette relation par \(\Delta x\) et \(\Delta y\). Faisant \(\Delta x \rightarrow 0\) et \(\Delta y \rightarrow 0\), on a, (calcul analogue à celui d’une seule variable) : \[\frac{Pr\{(X,Y)\in D\}}{\Delta x\Delta y} \rightarrow f(x,y) \qquad \text{densité de probabilité}\] \[\frac{F(x+\Delta x,~y+\Delta y)-F(x,~y+\Delta y)-F(x+\Delta x,~y)+F(x,y)}{\Delta y\Delta x}\rightarrow \frac{\partial^2F}{\partial x~\partial y}\]

Ce qui revient à dire que : \[f(x,y)=\frac{\partial^2F}{\partial x~\partial y}\]

7. Exemple. Étude complète

On considère le couple de variables aléatoires de densité de probabilité : \[f(x,y)=\frac{1}{\pi^2(x^2+y^2+x^2y^2+1)}\]

On voit immédiatement que l’on peut écrire : \[f(x,y)=\frac{1}{\pi(1+x^2)}\cdot\frac{1}{\pi(1+y^2)}\]

Et en déduire que : \[f(x,y)=f_x(x)~f_y(x)\]

avec : \[f_x(x)=\frac{1}{\pi(1+x^2)} \quad ; \quad f_y(y)=\frac{1}{\pi(1+y^2)}\]

Ce qui signifie que les variables X et Y sont indépendantes.

On peut par ailleurs vérifier (normalisation de la densité) que : \[\int\int_{R2}f(x,y)~dx~dy=1\]

On voit tout de suite que les variables d’intégration sont séparées, l’intégration double revenant au produit de deux intégrales identiques, de sorte que : \[I=\left\{\int_{-\infty}^{+\infty}\frac{du}{\pi(1+u^2)}\right\}^2=\frac{1}{\pi^2}\Bigl[Atan(u)\Bigr]_{-\infty}^{+\infty}=1\]

Enfin, la probabilité pour qu’un point donné tombe dans un carré élémentaire \([0<x<1 , 0<y<1]\) est égale à : \[J=\left\{\int_0^1\frac{du}{\pi(1+u^2)}\right\}^2=\frac{1}{\pi^2}\left(\frac{\pi}{4}\right)^2=\frac{1}{16}\]

8. Espérances mathématiques de sommes et de produits

Ces calculs d’intégration des espérances mathématiques de sommes et de produits sont élémentaires. Ils conduisent, ce qui peut se concevoir intuitivement, à :

\[\begin{aligned} E(X+Y)&=E(X)+E(Y) && \text{dans tous les cas} \\ E(XY)&=E(X)~E(Y) && \text{quand les variables sont indépendantes}\end{aligned}\]

9. Densité de probabilité d’une somme de variables indépendantes

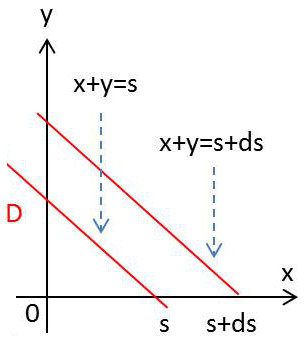On considère un couple \((X,Y)\) de variables aléatoires indépendantes et leur somme \(S=X+Y\).

On leur associe les densités de probabilité respectives : \[(X,Y) \ \rightarrow \ f(x,y) \quad ; \quad S=X+Y \ \rightarrow ~g(s)\]

On veut connaître l’expression de \(g(s)\) en considérant le domaine \(D\) délimité par les deux droites d’équation \(x+y=s\) et \(x+y=s+ds\)

La probabilité : \[Pr\{M(x,y)\in D\}=\int\int_Df(x,y)~dx~dy\]

s’exprime par : \[g(s)~ds=Pr(s<S<s+ds)=Pr(s<X+Y<s+ds)\]

On a donc : \[g(s)~ds=\int_{-\infty}^{+\infty}dx\int_{s-x}^{s-x+ds}f(x,y)~dy=ds\int_{-\infty}^{+\infty}f(x,s-x)~dx\]

Soit : \[g(s)=\int_{-\infty}^{+\infty}f(x,s-x)~dx\]

Si les variables sont indépendantes : \[f(x,s-x)=f_1(x)~f_2(s-x)\]

On a alors le produit de convolution que l’on recherchait : \[g(s)=\int_{-\infty}^{+\infty}f_1(x)~f_2(s-x)~dx=(f_1\star f_2)(s)\]