1. Position du problème
On peut concevoir qu’une variable aléatoire puisse être discrète ou continue localement. Mais pour pouvoir mener les calculs sous forme intégrale, il est nécessaire d’avoir recours au formalisme de la théorie des distributions. Pour faciliter l’exposé, nous raisonnerons sur un exemple.
2. Exemple
Bref rappel sur le formalisme des distributions
Pour exprimer la valeur prise par une fonction \(f(x)\) en un point unique de présence on écrit, en supposant choisi l’espace d’intégration \((-\infty,+\infty)\) :
\[f(x_0)=\int_{-\infty}^{+\infty}f(x)~\delta(x-x_0)~dx\]
 Exemple
Exemple
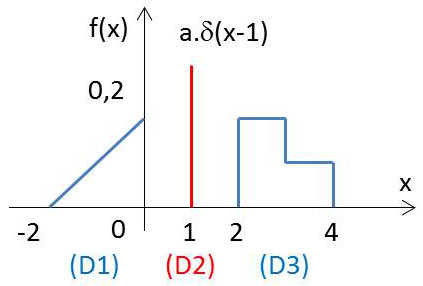
La densité de probabilité représentée graphiquement ci-contre comprend deux parties continues de part et d’autre d’une distribution de Dirac. La valeur de \(a\) n’étant pas connue, il faut la déterminer à partir de l’application de la règle de normalisation : \[\int_{-\infty}^{+\infty}f(x)~dx=1\]
On a une somme de trois intégrales dont l’une au sens des distributions : \[\int_{-\infty}^{+\infty}f_1(x)~dx+\int_{-\infty}^{+\infty}a~\delta(x-1)~dx+\int_{-\infty}^{+\infty}f_2(x)~dx=1\]
Deux intégrales ont donc valeur de surface, la troisième ayant valeur d’amplitude : \[S_1(0.2)+a+S_3(0.3)=1 \quad \text{donc} \quad a=0.5\]
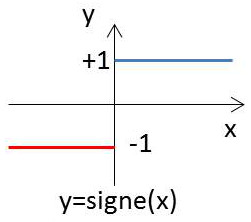 Supposons que l’on veuille à présent effectuer un changement de variable en appliquant à la variable \(x\) une pondération échelon.
Supposons que l’on veuille à présent effectuer un changement de variable en appliquant à la variable \(x\) une pondération échelon.
\(Y\) ne peut prendre que deux valeurs \((\pm 1)\) en respectant toujours la loi de probabilité définie pour \(x\).
D’après ce qui précède :
\[\begin{aligned} Pr(Y=-1)&=Pr(X<0)=S_1=0.2\\ Pr(Y=1)&=Pr(X>0)=0.5+0.3=0.8\end{aligned}\]
Il faut effectuer une dérivation pour calculer la densité de probabilité, mais au sens des distributions (la fonction échelon donnant une fonction impulsion de Dirac). On obtient donc : \[f_y(y)=0.2\ \delta(y+1)+0.8\ \delta(y-1)\]

