1. Introduction
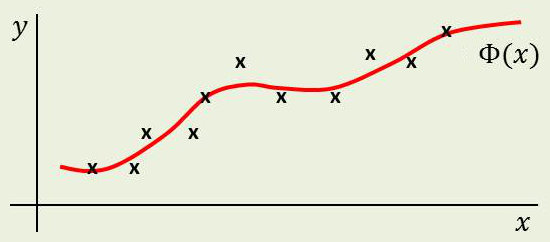 Ajuster les points issus de la mesure consiste à trouver une courbe qui s’en approche le plus : à lisser ces points.
Ajuster les points issus de la mesure consiste à trouver une courbe qui s’en approche le plus : à lisser ces points.
La technique la plus souvent utilisée pour y arriver est connue sous le nom de méthode des moindres carrés.
On dispose d’un certain nombre de points de coordonnées \(M_i(x_i,~y_i)\). La valeur des \(y_i\), paramètres mesurés, est entachée d’une erreur aléatoire, d’où une dispersion dans la distribution des points.
On cherche donc une relation de la forme \(y=\varphi(a_1~,a_2,~\dots,~a_n,~x)\) en essayant de déterminer les valeurs des coefficients \(a_i\) par approximation.
2. Principe de la méthode des moindres carrés
Des considérations pratiques (lois physiques connues ou répartitions des points) permettent d’estimer la forme de la fonction d’approximation. Par exemple :
\[\begin{aligned} &\text{Ajustement linéaire:} &&y=a~x+b &&\text{inconnues :}\quad a,~b \\ &\text{Ajustement puissance} &&y=a~x^b &&\text{inconnues :}\quad a,~b \\ &\text{Ajustement exponentiel} &&y=a~e^{b~x} &&\text{inconnues :}\quad a,~b \\ &\text{Ajustement logarithmique} &&y=a~ln(x)+b &&\text{inconnues :}\quad a,~b \\ &\text{Ajustement parabolique} &&y=a+~b~x+c~x^2 &&\text{inconnues :}\quad a,~b,~c \\ &\text{Ajustement cubique} &&y=a+b~x+c~x^2+d~x^3 &&\text{inconnues :}\quad a,~b,~c,~d \\ &\text{Etc.}\end{aligned}\]
Considérons une valeur quelconque de l’argument \(x_i\). Le résultat de l’expérience est une valeur aléatoire \(y_i\) répartie suivant une loi normale d’espérance mathématique \(\varphi(x)\) et d’écart type \(\sigma\) qui caractérise l’erreur de mesure. On supposera que cette erreur est la même en tout point : \[\sigma_1=\sigma_2=\dots=\sigma_n=\sigma\]
On associe alors à \(y_i\) une densité de probabilité : \[f_i(y_i)=\frac{1}{\sigma~\sqrt{2~\pi}}~\exp\Big\{-\frac{\big[y_i-\varphi(x_i)\big]^2}{2~\sigma^2}\Big\}\]
On suppose que l’expérience consiste en une série de mesures dans lesquelles les variables aléatoires \(\{\varphi_1,~\varphi_2,~\dots,~\varphi_n\}\) ont pris les valeurs \(\{y_1,~y_2,~\dots,~y_n\}\).
En raison de l’indépendance des mesures, la densité de probabilité est le produit des densités de probabilités : \[P=K\exp\Big\{-\frac{1}{2~\sigma^2}\sum_i\big[y_i-\varphi(x_i)\big]^2\Big\}\]
Les espérances mathématiques \(\varphi(x_i)\) doivent être choisies de telle sorte que cette densité soit maximale. Pour qu’il en soit ainsi, il faut que : \[\sum_{i=1}^n \big[y_i-\varphi(x_i)\big]^2 \quad\text{soit minimale.}\]
Compte tenu de la forme paramétrée \(y=\varphi(x,~a,~b,~c,~\dots)\), la recherche du minimum revient à la résolution d’un système linéaire d’équations d’où l’on extrait \(a,~b,~c,\) etc. : \[\left\{ \begin{aligned} &\sum_{i=1}^n \big[y_i-\varphi(x_i,~a,~b,~c,~\dots))\big]~\frac{\partial\varphi}{\partial a}\Big|_i=0 \qquad &&\frac{\partial\varphi}{\partial a}\Big|_i=\varphi'_a(x_i,~a,~b,~c,~\dots) \\ &\sum_{i=1}^n \big[y_i-\varphi(x_i,~a,~b,~c,~\dots))\big]~\frac{\partial\varphi}{\partial b}\Big|_i=0 &&\frac{\partial\varphi}{\partial b}\Big|_i=\varphi'_b(x_i,~a,~b,~c,~\dots) \\ &\dots &&\dots \end{aligned} \right.\]
3. Quelques exemples d’ajustements
3.1. Ajustement linéaire
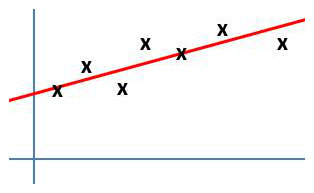 La répartition des points (\(x_i,~y_i\)) lors d’une expérience est représentée par le graphe ci-contre. Cette répartition suggère d’adopter un ajustement linéaire : \(y=ax+b\).
La répartition des points (\(x_i,~y_i\)) lors d’une expérience est représentée par le graphe ci-contre. Cette répartition suggère d’adopter un ajustement linéaire : \(y=ax+b\).
On a alors :
\[\begin{aligned} \frac{\partial y}{\partial a}=x\quad&\Rightarrow\quad \frac{\partial y}{\partial a}\Big|_i=x_i\\ \frac{\partial y}{\partial b}=1\quad&\Rightarrow\quad \frac{\partial y}{\partial b}\Big|_i=1\end{aligned}\]
On est alors amené à résoudre le système linéaire en a et b suivant : \[\left\{ \begin{aligned} &\sum_{i=1}^n \big[y_i-(a~x_i+b)\big]~x_i=0\\ &\sum_{i=1}^n \big[y_i-(a~x_i+b)\big]\times 1=0 \end{aligned} \right. \quad\Rightarrow\quad \left\{ \begin{aligned} &\sum_{i=1}^n x_i~y_i-a\sum_{i=1}^n x_i^2-b\sum_{i=1}^n x_i=0\\ &\sum_{i=1}^n x_i-a\sum_{i=1}^n x_i-b~n=0 \end{aligned} \right.\]
C’est-à-dire : \[\left\{ \begin{aligned} &a\sum x_i^2+b\sum x_i=\sum x_i~y_i\\ &a\sum x_i+b~n=\sum y_i \end{aligned} \right.\]
3.2. Ajustement parabolique
Pour un ajustement parabolique, on a :
\[\begin{aligned} &y=a~x^2+b~x+c\\ &\frac{\partial y}{\partial a}=x^2\quad;\quad\frac{\partial y}{\partial b}=x\quad;\quad\frac{\partial y}{\partial c}=1\end{aligned}\]
D’où les trois relations du système linéaire :
\[\begin{aligned} &a\sum x_i^2+b\sum x_i+c~n=\sum y_i\\ &a\sum x_i^3+b\sum x_i^2+c\sum x_i=\sum x_i~y_i\\ &a\sum x_i^4+b\sum x_i^3+c\sum x_i^2=\sum x_i^2~y_i\end{aligned}\]
4. Droite de régression
Pour fixer les idées, nous prendrons l’exemple de l’approximation linéaire \(y=a~x+b\).
On adopte le formalisme :
\[\begin{aligned} &m_x=\frac{\sum x_i}{n} &&m_y=\frac{\sum y_i}{n}\\ &\sigma_{xy}=\frac{\sum(x_i-m_x)(y_i-m_y)}{n} &&\sigma_x^2=\frac{\sum(x_i-m_x)^2}{n}\\ &a=\frac{\sigma_{xy}}{\sigma_x^2} &&b=m_y-a~m_x\end{aligned}\]
Par suite : \[y-m_y=\frac{\sigma_{xy}}{\sigma_x^2}~(x-m_x)\]
La droite \(D\) ainsi obtenue s’appelle droite d’estimation ou encore droite de régression ; le coefficient \(a\) s’appelle coefficient de régression ou coefficient d’estimation de y en x.
5. Notion d’anamorphose
L’anamorphose est une opération qui consiste à transformer un nuage de points quelconques en un nuage réparti sur une droite.
Prenons l’exemple d’un nuage de points de la forme \(y=A~e^{a~x}\).
On pourra écrire : \[\ln(y)=a~x+\ln(A)\]
Puis, en posant : \[Y=\ln(y)\quad;\quad\alpha=a\quad;\quad\beta=\ln(A)\]
Se trouver amené à résoudre : \[Y=\alpha~x+\beta\qquad\text{à partir du tableau } [x_i,~\ln(y_i)].\]
D’où (\(\alpha,~\beta\)), puis (\(a,~b\)).
6. Brèves notions sur la méthode de Mayer
La méthode de Mayer s’applique à un ajustement linéaire par une technique de dichotomie. Le tableau est séparé en deux parties, la première correspondant aux \(x\) négatifs et la seconde correspondant aux \(x\) positifs.
Raisonnons sur un exemple. Considérons le tableau suivant : \[\begin{matrix} x~: &-8 &-5 &-2 &2 &4 &8 &10\\ y~: &31 &41 &49 &58 &63 &76 &82 \end{matrix}\]
Scindons-le en deux tableaux : \[\begin{matrix} x_1~: &-8 &-5 &-2 &\quad &x_2~: &2 &4 &8 &10\\ y_1~: &31 &41 &49 & &y_2~: &58 &63 &76 &82 \end{matrix}\]
On obtient séparément :
\[\begin{aligned} \overline{x_1}&=-5 &&\overline{y_1}=121/3\\ \overline{x_2}&=6 &&\overline{y_2}=279/4\end{aligned}\]
Valeur du coefficient angulaire de la droite : \[a=\frac{\overline{y_2}-\overline{y_1}}{\overline{x_2}-\overline{x_1}}=2,67\]
On écrit ensuite que : \[y-\overline{y_2}=a~(x-\overline{x_2})=2,67~x+53,7\]
Cette méthode est moins précise que la méthode des moindres carrés, mais elle est beaucoup plus rapide.

