1. Séries trigonométriques

On considère la série : \[S=a_0+\sum_{n=1}^{\infty} a_n\cos(n~\omega~x)+b_n\sin(n~\omega~x)\qquad\text{n entier}\]

Si pour tout \(x\) cette série converge, la somme est une fonction périodique de \(x\), de période \(T\), donc de pulsation : \[\omega=\frac{2~\pi}{T}=2~\pi~n\]

Le terme correspondant à \(n=1\) est le fondamental. Le terme correspondant à \(n=2\) est l’harmonique 2, etc.

Les problèmes se posent de la manière suivante :

– Étant donné une fonction \(f(x)\) de période \(T\), pour tout \(x\), existe-t-il une série du type \(S\) dont \(f(x)\) soit la somme ? Si tel est le cas, \(S\) est appelée série de Fourier de \(f(x)\).

– \(f(x)\) étant définie sur \([a,~b]\), existe-t-il une série \(S\) telle que \(f(x)\) en soit la somme sur l’intervalle \([a,~b]\) ?

2. Série de Fourier d’une fonction périodique

Supposons le problème résolu. Étant donné \(f(x)\) de pulsation \(\omega\), on a : \[f(x)=a_0+\sum_{n=1}^{\infty} a_n\cos(n~\omega~x)+b_n\sin(n~\omega~x)\]

Nous supposons de plus \(S\) uniformément convergente sur \([0,~T]\), \(T\) étant la période de \(f(x)\). Pour fi xer les idées, prenons \(T=\pi\), c’est-à-dire \(\omega=1\).

Calcul des coefficients

On intègre de 0 à \(T\) : \[\int_0^{2\pi} f(x)~dx=\int_0^{2\pi} a_0~dx+\int_0^{2\pi}\sum a_n\cos(n~\omega~x)~dx+\int_0^{2\pi}\sum b_n\sin(n~\omega~x)~dx\]

Et en permutant les sommations : \[\int_0^{2\pi} f(x)~dx=\int_0^{2\pi} a_0~dx+\sum\int_0^{2\pi} a_n\cos(n~\omega~x)~dx+\sum\int_0^{2\pi} b_n\sin(n~\omega~x)~dx\]

On a immédiatement : \[\int_0^{2\pi} f(x)~dx=2~\pi~a_0 \quad\Rightarrow\quad a_0=\int_0^{2\pi} f(t)~dt\]

Multiplions à présent les deux termes de la relation par une fonction continue, par exemple \(\cos(n~x)\). Elle reste uniformément convergente :

\[\begin{aligned} \int_0^{2\pi} f(x)\cos(n~x)~dx=\int_0^{2\pi}a_0\cos(n~x)~dx &+\sum_{p=1}^{\infty}\int_0^{2\pi}a_p\cos(p~x)\cos(n~x)~dx \\ &+\sum_{p=1}^{\infty}\int_0^{2\pi}a_p\cos(p~x)\cos(n~x)~dx\end{aligned}\]

C’est-à-dire : \[\int_0^{2\pi} f(x)~\cos(n~x)~dx=0+a_n\int_0^{2\pi}\cos^2(n~x)~dx+0\]

On obtient : \[a_n=\frac{1}{\pi}\int_0^{2\pi} f(t)~\cos(n~t)~dt\quad;\quad b_n=\frac{1}{\pi}\int_0^{2\pi} f(t)~\sin(n~t)~dt\]

Et dans le cas général

\[\begin{aligned} a_0&=\frac{1}{T}\int_0^T f(t)~dt\\ a_n&=\frac{1}{T}\int_0^T f(t)~\cos(n~\omega~t)~dt\quad;\quad b_n=\frac{1}{T}\int_0^T f(t)~\sin(n~\omega~t)~dt\end{aligned}\]

3. Expression complexe du développement en série de Fourier

Reprenons l’expression première : \[f(x)=a_0+\sum_{n=1}^{\infty} a_n\cos(n~\omega~x)+b_n\sin(n~\omega~x)\]

Utilisons les expressions complexes des fonctions circulaires : \[\cos~x=\frac{e^{i~x}+e^{-i~x}}{2}\quad;\quad\sin~x=\frac{e^{i~x}+e^{-i~x}}{2~i}=(-i)~\frac{e^{i~x}-e^{-i~x}}{2}\]

Et posons : \[C_n=\frac{a_n-i~b_n}{2}\quad;\quad C_{-n}=\frac{a_n+i~b_n}{2}\]

Toutes identifications faites, on obtient les expressions générales :

\[\begin{aligned} f(x)&=\sum_{n=-\infty}^{+\infty}C_n~\exp(i~n~\omega~x)\\ C_n&=\frac{1}{T}\int_0^T f(t)~\exp(-i~n~\omega~t)~dt\end{aligned}\]

4. Convergence de la série de Fourier

Rappelons que si une fonction \(f\) est continue presque partout sur \([a,~b]\) et, si elle est de plus bornée en valeur absolue sur \([a~,~b]\), on dira qu’elle est de type CB (continue bornée).

Si deux fonctions \(f\) et \(g\) du type CB sont égales presque partout sur \([a,~b]\), alors : \[\int_a^b f(x)~dx=\int_a^b g(x)~dx\]

Théorème 1

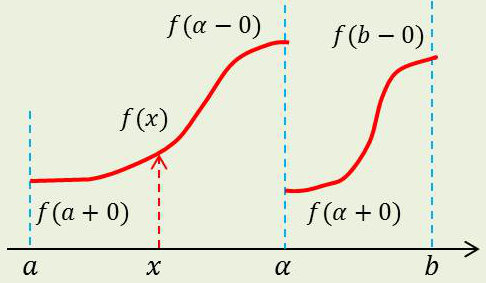Si une fonction \(f(x)\) est monotone par morceau sur le fermé \([a,~b]\)  :

Si \(f(x)\) est de type CB sur \([a,~b]\), si \(\forall x\in [a,~b]\) : \[f(x)=\frac{f(x+0)+f(x-0)}{2}\]

Si on a : \[f(a)=f(b)=\frac{f(a+0)+f(b-0)}{2}\]

alors la série de Fourier de \(f(x)\) sur \([a,~b]\) tend vers \(f(x\)), \(\forall x\in [a,~b]\).

Théorème 2

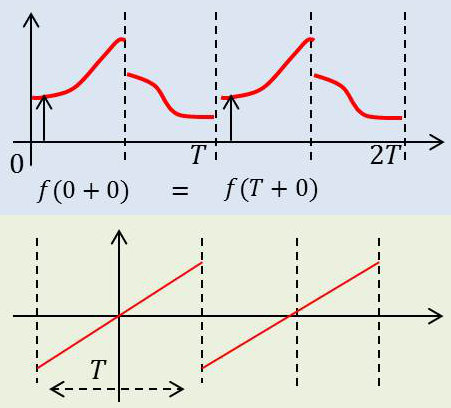
Si une fonction \(f\) du type CB est égale à la somme de sa série de Fourier et si de plus \(f\) est continue, la série de Fourier converge uniformément vers la fonction \(f\).

Noter que la valeur de la série de Fourier est nulle aux bornes de la période (figure 2).

5. Coefficients de Fourier de translatée de fonction périodique

Soit \(f(x)\) de période\(T\) et supposons qu’il existe une série de Fourier :

\[\begin{aligned} f(x)&=\sum_{n=-\infty}^{+\infty}C_n~\exp(i~n~\omega~x)\\ C_n&=\frac{1}{T}\int_0^T f(t)\exp(-i~n~\omega~t)~dt\end{aligned}\]

La translatée de \(f(x)\) est \(g(x) = f(x + h)\), \(h\) étant une constante : \[C_n(g)=\frac{1}{T}\int_0^T g(x)~\exp(-i~n~\omega~x)~dx=\frac{1}{T}\int_0^T f(x-h)~\exp(-i~n~\omega~x)~dx\]

Posons \(u = x - h\) : \[C_n(g)=\frac{1}{T}\int_{-h}^{T-h}f(u)~\exp\{-i~n~\omega~(u+h)\}~du\]

Or, \(f(u)\) est périodique :

\[\begin{aligned} C_n(g)&=\frac{1}{T}~\Big\{\int_0^T f(u)~\exp(-i~n~\omega~u)~du\Big\}~\exp(-i~n~\omega~h) \\ C_n(g)&=C_n~\exp(-i~n~\omega)\end{aligned}\]

6. Coefficients de Fourier de dérivée de fonction

Soit une fonction \(f\) continue admettant une dérivée première \(f'\) de type CB : \[C_n(f')=\frac{1}{T}\int_0^T f'(x)~\exp(-i~n~\omega~x)~dx\]

Intégrons par parties : \[C_n(f')=\frac{1}{T}~\big\{f(x)~\exp(-i~n~\omega~x)\big\}_0^T+\frac{1}{T}\int_0^T f(x)~(i~n~\omega)~\exp(-i~n~\omega~x)~dx\]

Le premier terme étant nul : \[C_n(f')=(i~n~\omega)~C_n(f)\]

Soit une fonction continue périodique admettant des dérivées continues jusqu’au \((k-1)^{\text{ième}}\) ordre et telle que la dérivée \(k^{\text{ième}}\) soit du type CB, on aura : \[C_n(f^{(k)})=(i~n~\omega)^k~C_n(f)\qquad\text{et inversement :}\quad C_n(f]=\frac{1}{(i~n~\omega)^k}~C_n(f^{(k)})\]

On a \(C_n(f^{(k)})\rightarrow 0\) quand \(n\rightarrow\infty\), car c’était le cas pour \((a_n,~b_n)\), donc pour \((a_n\pm i~b_n)\). De même, \(C_n(f)\rightarrow 0\) quand \(n\rightarrow\infty\), mais beaucoup plus vite en raison du facteur fortement décroissant.

Donc, plus une fonction est dérivable, plus vite ses coefficients de Fourier tendent vers zéro quand \(n\) tend vers l’infini. Ainsi, plus une fonction est régulière, plus ses harmoniques supérieurs pourront être négligés.

7. Produit de convolution

Soit deux fonctions \(f(x)\) et \(g(x)\) périodiques \(T\) et de type CB. On appelle produit de convolution de \(f(x\)) et \(g(x)\) la fonction \(h(x)\) telle que : \[h(x)=\frac{1}{T}\int_0^T f(t)~g(x-t)~dt \quad\text{notée :}~~h(x)=f(x)\star g(x)\]

7.1. Propriétés

On démontre les propriétés suivantes :

• Continuité : \(h(x)\) est une fonction continue.

• Commutativité : \(h(x)=f(x)\star g(x)=g(x)\star f(x)\)

• Associativité : \(f\star(g\star h)=(f\star g)\star h\)

• Périodicité : si \((f~,~g)\) périodiques \(T\), alors \(h(x)\) est périodique \(T\).

7.2. Coefficients de Fourier de la convolution

De par les définitions de \(C_n\) et de \(h(x)\), il vient : \[C_n[h(x)]=\frac{1}{T}\int_0^Th(x)\exp(-i~n~\omega~x)~dx=\frac{1}{T^2}\int_0^Tdx\int_0^T f(t)~g(x-t)~\exp(-i~n~\omega~x)~dt\]

Comme les limites sont constantes et finies, la permutation du signe intégral est possible. De sorte que : \[C_n[h(x)]=\frac{1}{T^2}\int_0^Tdt\int_0^T f(t)~g(x-t)~\exp(-i~n~\omega~x)~dx\]

Posons \(u = x-t\), on a : \[C_n[h(x)]=\frac{1}{T^2}\int_0^Tdt\int_{-t}^{T-t} f(t)~g(u)~\exp[-i~n\omega(u+t)]~du\]

\(\exp[-i~n\omega(u+t)]\) : fonction périodique T de même que \(f(t\)) et \(g(t)\) : \[C_n[h(x)]=\frac{1}{T}\int_0^T dt~f(t)~\exp(-i~n~\omega~t)\times\frac{1}{T}\int_0^T g(u)~\exp(-i~n~\omega~u)~du\]

On a donc : \[C_n(h)=C_n(f)~C_n(g)\]