1. Théorème des résidus

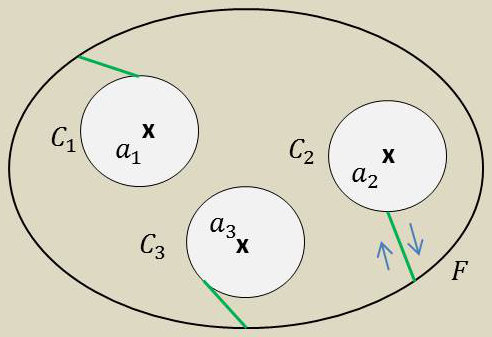Soit un point singulier \(a\) non critique (pôle ou point essentiel). Nous savons qu’au voisinage de ce point on peut développer la fonction \(f(z)\) en série de Laurent dans le cas d’un pôle simple : \[f(z)=\frac{b_1}{(z-a)}+H(z-a)\]

Le coefficient \(b_1\) est appelé résidu de \(f(z)\) au point \(a\). Il représente la vraie valeur de \(f(z)\) en ce point, c’est-à-dire que (tous les autres termes s’annulant) : \[b_1=\big[(z-a)~f(z)\big]_{z=a}\]

En application du théorème de Cauchy, on démontre que : \[\int_F f(z)~dz=2~i~\pi~b_1\]

En effet : \[\int_C\frac{f(z)~dz}{(z-a)}=2~i~\pi~f(a)\]

De même : \[\int_C\frac{b_1dz}{(z-a)}=2~i~\pi~b_1\]

On peut généraliser à un nombre quelconques de pôles simples (ou même multiples) : \[\int_C f(z)~dz=2~i~\pi~\sum_k \text{Résidus}(a_k)\]

Remarque. Calcul pratique

On peut écrire : \[f(z)~(z-a)=b_1+(z-a)~H(z-a)\]

Comme \(z = a\) est un pôle de \(f(z\)), on peut poser : \[f(z)=\frac{P(z)}{Q(z)}\qquad\Rightarrow\qquad Q(z)=(z-a)~K(z)\]

On a alors : \[b_1=\frac{P(a)}{Q(a)}\]

Par ailleurs : \[Q'(z)=K(z)+(z-a)~K'(z)\qquad\text{donc :}\quad Q'(a)=\big[K(a)\big]_{z=a}\]

Il s’ensuit que : \[b_1=\text{Résidu}(a)=\frac{P(a)}{Q'(a)}\]

Résultat fondamental qui sera utilisé directement pour le calcul du résidu associé à un pôle simple.

2. Intégrales à pôles simples. Calcul pratique

Soit à calculer l’intégrale : \[I=\int_{-\infty}^{+\infty}\frac{dx}{1+x+x^2}\]

On commence par considérer la fonction analytique associée : \[f(z)=\frac{1}{1+z+z^2}\]

Les pôles simples (ou zéros du dénominateur) ont pour valeurs : \[z=\frac{-1\pm i~\sqrt{3}}{2}\]

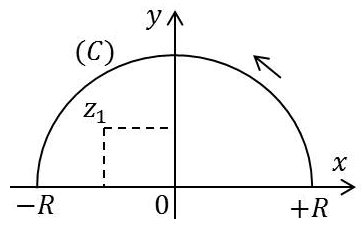
Le contour choisi est représenté ci-contre.

Un seul pôle est intéressant. C’est celui présent à l’intérieur du contour, c’est-à-dire : \[z_1=\frac{-1+ i~\sqrt{3}}{2}\]

Le contour d’intégration comprend :

– l’axe réel, celui qui correspond à l’intégration attendue ;

– le demi-cercle dont le rayon \(R\) doit tendre vers l’infini, parcours sur lequel le lemme de Jordan s’applique facilement (l’intégrale devenant nulle sur ce contour, car la forme devient infiniment petite en \(1/R^2\)) : \[b_1=\Big[\frac{1}{1+2~z}\Big]_{z=z_1}=\frac{1}{1+~2~z_1}=\frac{1}{i~\sqrt{3}}\]

Il vient alors : \[I=2~i~\pi~b_1=\frac{2~\pi}{\sqrt{3}}\]

3. Pôle multiple

S’il s’agit d’un pôle d’ordre n, le développement en série sera : \[f(z)=\frac{b_n}{(z-a)^n}+\cdots+\frac{b_1}{(z-a)}+H(z-a)\]

On doit alors former : \[f(z)~(z-a)^n=b_n+\cdots+b_1~(z-a)^{n-1}+\cdots\]

On voit que \(b_1\) est le coefficient de \((z-a)^{n-1}\) à un facteur près, c’est-à-dire que : \[b_1=\frac{1}{(n-1)!}~\frac{d^{n-1}}{dz^{n-1}}~\big[f(z)~(z-a)^n\big]_{z=a}\]

4. Point singulier essentiel

Dans le cas d’un point singulier essentiel, il faut effectuer le développement en série de Laurent et extraire directement le résidu à partir de l’expression de cette série.

5. Quelques recettes

Nous donnons ici quelques éléments sur les changements de variable permettant de simplifier les calculs et des choix judicieux de contours.

5.1. Type 1

\[I=\int_0^{2\pi} R[sin(t),~cos(t)]~dt\]

\(R\) est une fraction rationnelle à deux variables : \[u=\sin t\quad\text{et}\quad v=\cos t\]

On pose \(z=e^{i~t}\) et on intègre en prenant comme contour le cercle unité, parcouru dans le sens direct.

Exemple

\[I_1=\int_0^{2\pi} \frac{dt}{a+\cos t}\qquad a\in \mathbb R~~;~~ a>1\]

On trouve : \[I_1=\frac{2~\pi}{\sqrt{a^2-1}}\]

5.2. Type 2

\[I=\int_{-\infty}^{+\infty} R(x)~dx\]

\(R\) est une fraction rationnelle mise sous forme irréductible \(P/Q\) dans laquelle \(P\) et \(Q\) sont des polynômes tels que :

• leurs degrés sont tels que \(deg(Q)-deg(P)>1\) ;

• le polynôme \(Q\) ne possède pas de zéros sur l’axe réel ;

• les pôles de \(R\) sont les zéros de \(Q\) et ils ne sont pas réels.

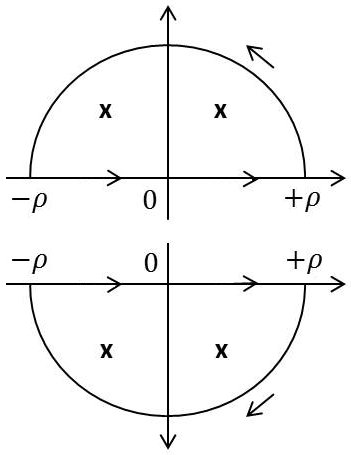
On peut intégrer suivant deux contours possibles sur une partie des pôles (en appliquant aux cercles le lemme de Jordan).

Exemple

\[J=\int_{-\infty}^{+\infty}\frac{1}{1+x^{2~n}}\qquad n\in \mathbb N^*\]

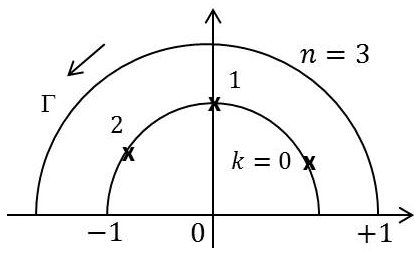Les pôles de \(R(z)\) sont les zéros de : \[R(z)=(z^{2~n}+1)^{-1}\]

C’est-à-dire : \[z_k=\exp\Big(\frac{i~(2~k+1)~\pi}{2~n}\Big)\qquad k=0,~1,~\dots,~(n-1)\]

Par application du lemme, l’intégrale sur le cercle est nulle et il vient :

\[\begin{aligned} &J=2~i~\pi~\sum_k\text{Résidus}=2~i~\pi~\sum_{k=0}^{n-1}\Big\{-\frac{z_k}{2n}\Big\} \\ &J=\frac{\pi}{n~\sin(\pi/2~n)}\end{aligned}\]

5.3. Type 3

\[I=\int_{-\infty}^{+\infty} R(x)~e^{i~t~x}~dx\]

\(R\) est une fraction rationnelle et on fait les mêmes hypothèses sur \(R\) que pour le deuxième type. On pose alors : \[f(z)=R(z)~e^{i~t~z}\]

et on adopte les mêmes types de contours que pour le type 2, à savoir :

• contour supérieur si \(t\geq 0\) ;

• contour inférieur si \(t\leq 0\).

5.4. Type 4

\[J=\int_{-\infty}^{+\infty} R(\sinh x,~\cosh x)~e^{i~t~x}~dx\]

\(R\) est une fraction rationnelle et \(t\) une variable réelle.

Raisonnons sur un exemple pour fixer les idées : \[J=\int_{-\infty}^{+\infty}\frac{e^{i~t~x}}{\cosh x+\sinh x}~dx\quad;\quad a\geq 0\]

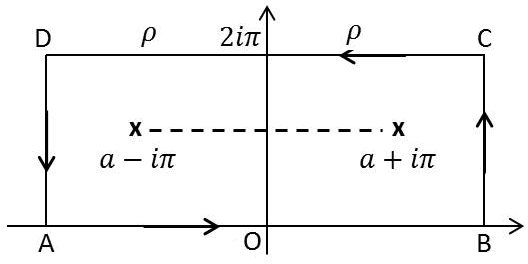On intègre une fonction \(f(z\)) en ayant remplacé \(x\) par \(z\) et en choisissant le contour ci-contre.

À l’intérieur du contour il y a deux pôles simples.

Le contour comporte quatre intégrations dont deux correspondent (au signe près) à l’intégrale proposée et dont deux donneront un résultat nul (contours \(BC\) et \(DA\)) en faisant tendre \(\rho\) vers l’infini.

Il suffit d’appliquer le théorème des résidus. Tous calculs faits : \[I=\frac{2~\pi~\sin(t~a)}{\sinh(\pi~t)~\sinh(a)}\]

5.5. Type 5

\[I=\int_a^{\infty} R(x)~dx\]

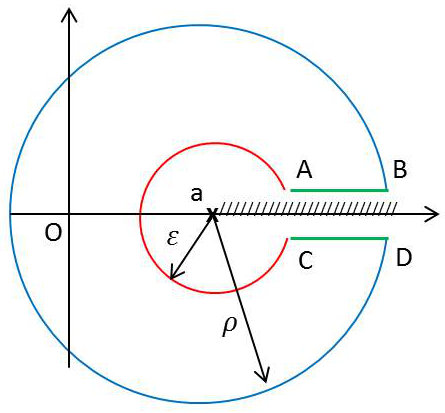On suppose que \(R=P/Q\) est une fraction rationnelle sans pôle sur le demi-axe \([a,~\infty [\) et que \(\deg(Q)-\deg(P)>1\).

Ici, la fonction de variable complexe considérée n’est plus \(R(z)\), mais : \[f(z)=R(z)~\ln(z-a)\]

où la détermination du logarithme est telle que : \[\arg(z-a)\in~]0,~2~\pi[\]

On intègre sur le contour ci-contre.

Le lemme de Jordan s’applique alors aux contours circulaires en faisant tendre les rayons vers zéro ou vers l’infini suivant qu’il s’agisse du petit ou du grand cercle.

On peut alors démontrer que : \[I=\int_a^{\infty} R(x)~dx=-\sum \text{Résidus}\{R(z)~\ln(z-a)\}\]

5.6. Type 6

\[I=\int_0^{\infty} x^{\alpha}~R(x)~dx\]

Le paramètre \(\alpha\) est réel ou complexe, non entier et \(R\) est une fraction rationnelle sans pôle sur le demi axe \([0,~\infty[\).

L’intégrale est supposée absolument convergente.

La fonction complexe considérée est alors : \[f(z)=z^{\alpha}~R(z)=\exp\{\alpha~\ln(z)\}~R(z)\]

On retrouve le contour précédent mais cette fois avec l’origine comme point critique.