1. Dissociation électrolytique

Par électrolyse, l’énergie électrique peut être convertie en énergie chimique. L’opération inverse est effectuée dans les piles et les accumulateurs.

En plongeant deux conducteurs portés à des potentiels différents (électrodes) dans un liquide pur non métallique, on constate que le liquide se comporte comme un isolant. Les solutions, au contraire, peuvent se comporter comme des conducteurs.

Le passage du courant s’accompagne d’un transport de matière. En règle générale, dans une solution aqueuse, il y a apparition :

• de métal (ou d’hydrogène) sur l’électrode négative (anode) (pôle [+] du générateur) ;

• de métalloïde sur l’électrode positive (cathode) (pôle [–] du générateur).

Une telle solution est un électrolyte. La conduction s’effectue par transport d’ions.

Dans les sels, acides ou bases fortes, une grande partie des forces de liaison est de nature électrostatique. Dans un diélectrique de constante \(\varepsilon_r\), ces forces sont divisées par \(\varepsilon_r\). Dans l’eau principalement (\(\varepsilon_r=\) 80), mais également dans l’alcool (\(\varepsilon_r=\) 24), dans l’ammoniaque (\(\varepsilon_r=\) 17) et dans de nombreux autres liquides, il y a dissociation en ions.

La dissociation est pratiquement complète pour les électrolytes forts (loi de Raoult).

À l’extérieur de la cuve à électrolyse, le sens de circulation des électrons est imposé par le générateur qui agit comme une pompe à électrons. Il les aspire de l’anode et les refoule vers la cathode. Les électrons circulent de l’anode vers la cathode.

À l’intérieur, la circulation des ions assure le passage du courant électrique. Les cations [+] circulent dans le même sens que le courant ; ils se dirigent vers la cathode. Les anions [–] circulent en sens inverse : ils se dirigent vers l’anode.

2. Réactions chimiques sur les électrodes

Les réactions chimiques sur les électrodes sont produites par le passage du courant. Sans insister sur les phénomènes calorifiques qui peuvent se produire sur les électrodes, il est à noter un effet analogue à l’effet Peltier avec dégagement ou absorption de chaleur à l’interface électrode – solution selon le sens du courant.

Certaines énergies de réactions \(W\) sont définies à une constante près notée \(eV_0\). Les énergies \(W\) pouvent être mesurées par différence. Par convention, \(V_0\) est la différence de potentiel entre une électrode à hydrogène et une solution normale d’ions \(H^+\).

Nous considèrerons quatre types de conduction électrolytique.

2.1. Dépôt de cation et électrodes de même métal cation

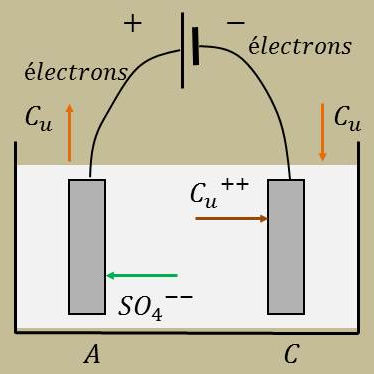  \[2~e^{-}\leftarrow C_u\quad||\leftarrow SO_4^{2-}~C_u^{2+}\rightarrow||\quad C_u\leftarrow 2~e^{-}\] \[\quad\rm anode(+)\qquad\qquad solution\qquad\qquad cathode(-)\]

Sur la cathode du cuivre, se dépose : \[C_u^{2+}+2~e^{-}\quad\rightarrow\quad Cu+2~W_1\]

Sur l’anode du cuivre, se dissous en même quantité : \[SO_4^{2-}+C_u\rightarrow[SO_4^{2-}+C_u^{2+}]+2~e^{-}-2~W_1\]

Il est commode de donner \(W_1\) en électrons-volt (eV) par charge élémentaire. Ici, si la solution de \(SO_4C_u\) est normale : \[W_1=eV_0+0,34~\rm eV\quad(\text{par charge élémentaire})\]

Noter que \(W1\) n’est pas le travail d’extraction d’un électron du métal dans le vide, mais le travail d’extraction du métal dans la solution normale de \(SO_4Cu\).

2.2. Dépôt de cation de même métal et anode attaquable

\[2~e^{-}\leftarrow Z_n\quad||\leftarrow SO_4^{2-}C_u^{2+}\rightarrow||\quad C_u\leftarrow 2~e^{-}\] \[\quad\rm anode(+)\qquad\qquad solution\qquad\qquad cathode(-)\]

Sur la cathode du cuivre, se dépose : \[Cu^{2+}+2~e^{-}\quad\rightarrow\quad Cu+2~W_1\]

Sur l’anode, du zinc, entre en solution : \[SO_4^{2-}+Zn\rightarrow[SO_4^{2-}+Zn^{2+}]+2~e^{-}-2~W_2\]

Dans une solution normale de \(Zn^{2+}\), on mesure : \[W_2=eV_0-0,76~\rm eV\]

2.3. Dépôt de cation sur cathode de même métal et anode inattaquable

\[2~e^{-}\leftarrow Pt\quad||\leftarrow SO_4^{2-}~Cu^{2+}\rightarrow||\quad Cu\leftarrow 2~e^{-}\] \[\quad\rm anode(+)\qquad\qquad solution\qquad\qquad cathode(-)\]

Sur la cathode du cuivre, se dépose : \[Cu^{2+}+2~e^{-}\quad\rightarrow\quad Cu+2~W_1\]

Sur l’anode : \[SO_4^{2-}+H_2O\rightarrow[SO_4^{2-}+2~H^+]+\frac{1}{2}~O_2^{\uparrow}+2~e^{-}-2~W_3\]

L’ion \(SO_4^{2-}\) ne réagit pas sur le platine mais sur l’eau pour donner de l’acide sulfurique dissocié et de l’oxygène qui se dégage.

NB : Si la cathode était également en platine, elle se recouvrirait de cuivre et on serait ramené au même schéma.

2.4. Conduction électrolytique sans dépôt de cation

\[e^{-}\leftarrow Pt\quad||\leftarrow~Cl^-~Na^+\rightarrow||\quad Pt \leftarrow e^{-}\] \[\quad\rm anode(+)\quad\qquad solution\qquad\quad cathode(-)\]

Sur la cathode : \[Na^+ +e^{-}+~H_2O\quad\rightarrow\quad[Na^+ +OH^-]+\frac{1}{2}~H_2^{\uparrow}+W_4\]

Sur l’anode : \[Cl^-+\frac{1}{2}~H_2O\quad\rightarrow\quad[Cl^-+H^+]+\frac{1}{4}~O_2^{\uparrow}+e^{-}-W_5\]

Il se dégage de l’hydrogène sur la cathode et de l’oxygène sur l’anode (dissociation de l’eau dans un voltamètre).

Les ions \(OH^-\) et \(H^+\) sont en équilibre avec l’eau : \[OH^-+H^+\leftrightarrow~H_2O\qquad\text{avec :}\quad[OH^-]\cdot[H^+]=10^{-14}\]

Les phénomènes sont souvent compliqués par :

• l’absorption de l’anode et la réduction de la cathode (par exemple, dans les accumulateurs au plomb : \(P_bO,~Pb_3O_4,~Pb_5O_4\dots\) ) intéressant pour réaliser une couche mince d’oxyde sur aluminium ;

• les autres réactions produites au voisinage des électrodes (exemple : formation d’eau de Javel dans l’électrolyse de \(C_lN_a\) ).

3. Différence de potentiel électrode – solution

On peut constater que le potentiel d’une électrode n’est pas le même que celui de la solution dans laquelle elle plonge. Ce potentiel dépend de la concentration de la solution en cations, mais il est indépendant de la nature de l’anion tant que la valence du cation ne change pas.

Par exemple, pour les solutions de \(C_u^{2+}\), on doit se méfier des ions \(C_u^+\) ou de complexes de sels peu solubles constitués avec \(C_u\).

Rappelons à titre d’exemple, la réaction : \[Cu^{2+}\quad\rightarrow\quad Cu-2~e^{-}+2~W_1\]

avec, pour une solution normale de \(Cu^{2+}\) , \(W_1=0,34~\rm eV\) par charge élémentaire. La réaction est exoénergétique.

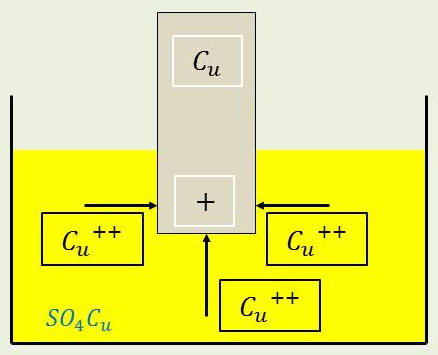Dès que le cuivre est plongé dans la solution, une petite quantité d’ions vient se déposer par affinité chimique, apportant des charges positives et accroissant le potentiel de l’électrode en cuivre.

Ce potentiel d’équilibre est atteint (à l’effet Peltier près) lorsque l’énergie chimique que gagnerait un ion \(Cu^{2+}\) à se combiner avec deux électrons sur la cathode est égal au travail électrostatique qu’il faudrait fournir pour amener cet ion au potentiel \(V_1\) de l’électrode par rapport à la solution.

Les ions \(Cu^{2+}\) se précipitent par affinité physicochimique sur \(Cu\) qui se charge positivement jusqu’à ce que la répulsion coulombienne arrête cette migration.

Soit, pour une solution normale : \[eV_1=W_1-eV_0\quad;\quad V_1=V_0+0,34~\rm V\]

Si la solution n’est plus normale, la statistique de Maxwell-Boltzmann enseigne que la concentration de l’atmosphère ionique de valence \(Z\) est proportionnelle à \(\exp(-Z~W_1/k~T)\).

On a donc : \[\begin{aligned} W_1&=(W_1)_{normale}~\frac{-k~T}{Z}~\ln[Cu^{2+}]\\ V_1&=V_0+0,34+\frac{k~T}{Z}~\ln[Cu^{2+}] \end{aligned}\]

• \(n\) : électrovalence de l’ion (ici \(n=2\))

• \(Cu^{2+}\) : concentration en valence-gramme / litre

À température ambiante : \[V_1=V_0+0,34+\frac{0,058}{2}~\log[Cu^{2+}]\]

4. Électrolyse

Si un nombre \(N\) d’ions arrive sur une électrode, la charge correspondante est \(N~(n~e)\) en considérant que \((n~e)\) est la charge de chaque ion et \(n\) la valence de l’ion (1 pour \(Na^+\), 2 pour \(Cu^{2+}\) et 3 pour \(Al^{3+}\)). En particulier, le transport de 1 atome gramme (masse A) s’effectue avec transport d’une charge \(\mathcal{N}~(n~e)\) (\(\mathcal{N}\) : nombre d’Avogadro).

Adoptant les deux définitions suivantes :

• \(A/Z\) : valence gramme (masse atomique \(A\) / valence \(Z\))

• et \(\mathcal{N}e=96~540~\rm C~mol^{-1}\) (coulombs par mole): constante de Faraday (produit de la charge élémentaire par le nombre d’Avogadro),

l’expérience montre effectivement qu’un faraday décompose une demi-molécule gramme d’eau, dépose une valence gramme de n’importe quel métal sur une cathode, est produit par les réactions chimiques portant sur une valence gramme et réalisées lentement dans les piles et les accumulateurs.

Par une règle de trois, on trouve que la quantité de corps pur correspondant au passage d’une intensité de courant \(I\) pendant un temps \(t\) (et donc une charge \(Q = I~t\)) est : \[m=\frac{1}{96~540}~\frac{A}{n}~I~t\]

Comme pour un gaz, la conduction et la mobilité dues à un type d’ions peuvent se mettre sous la forme : \[\sigma_i=\frac{n~z^2~e^2~\tau}{M}\quad;\quad\mu_i=\frac{z~e~\tau}{M}\]

• \(M\)  :  masse de l’ion

• \(\tau\)  :  durée moyenne entre deux chocs

• \(n\)  :  nombre d’ions / unité de volume

Dans un gaz, \(\sigma_i\approx 10^{-13}~\Omega~\rm m^{-1}\).

Pour un gaz léger, \(\mu_i\approx 10^{-2}~\rm m^2~V^{-1}~s^{-1}\).

Pour un gaz lourd, \(\mu_i\approx 10^{-3}~\rm m^2~V^{-1}~s^{-1}\).

Dans les liquides, la vitesse d’agitation thermique est comparable, mais le libre parcours moyen est, à température ambiante, de l’ordre des distances interatomiques (\(10^{-9}\) m au lieu de \(10^{-6}\) m pour les gaz dans les conditions normales). La mobilité est donc de l’ordre de \(10^{-7}~\rm m^2~V^{-1}~s^{-1}\).

5. Nuage écran. Théorie de Debye et Huckel

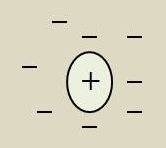Considérons un ion positif dans un électrolyte. Son champ coulombien attire des ions négatifs qui, en moyenne, forment autour de l’ion [+] un nuage de charge négative qui neutralise à distance le champ électrique.

La dimension du nuage et la modification d’énergie de l’ion qui en résulte joue un rôle important dans la théorie des électrolytes, mais on en retrouve les propriétés dans les métaux, les semi-conducteurs et les plasmas.

L’électrolyte est supposé contenir des ions \(z^+\) et \(z^-\). On appelle \(n_1\) et \(n_2\) les nombres moyens d’ions [+] et [-] par unité de volume. La condition d’électroneutralité s’écrit : \[n_1~z^+=n_2~z^-\]

D’où la densité de charge électrique : \[\rho=e~(z^+~n^+-z^-~n^-)\]

et l’équation de Poisson (potentiel) : \[\Delta V=-\frac{\rho}{\varepsilon}\]

Cette équation autour d’un ion (+), résolue en symétrie sphérique, est du type : \[\Delta V=\frac{1}{r^2}~\frac{d}{dr}\Big(r^2~\frac{dV}{dr}\Big)\]

Il vient, compte tenu de la neutralité électronique: \[\begin{aligned} &\frac{1}{r^2}~\frac{d}{dr}\Big(r^2\frac{dV}{dr}\Big)=\chi^2~V \\ &\chi^2=\frac{e^2}{\varepsilon~k~T}~\{n_1~(z^+)^2+n_2~(z^-)^2\} \end{aligned}\]

D’où la solution : \[V=A~\frac{\exp(-\chi~r)}{r}+A'~\frac{\exp(\chi~r)}{r}\]

On doit avoir \(A’=0\), car \(V\) doit être fini à l’infini. Le premier terme subsiste.

Il s’ensuit que : \[E=-\frac{dV}{dr}=A~\frac{\exp(-\chi~r)}{r}~\Big(\frac{1}{r}+\chi\Big)\]

Il faut se rendre compte que ce calcul n’est correct que si \(r\) n’est pas trop petit, sinon les énergies d’interaction comporteraient des termes de répulsion interdisant l’interpénétration des ions. Nous couperons donc arbitrairement les \(r\) petits à une valeur \(a\), dite rayon d’interpénétration des ions.

De plus, le champ est connu pour \(r=a\) : \[E_a=\frac{e~z^+}{4\pi~\varepsilon~a^2}\]

Le raccord avec la solution générale donne \(A\) : \[A=\frac{e~z^+}{4\pi~\varepsilon}~\frac{\exp(\chi~a)}{1+\chi~a}\]

On a alors : \[V=\frac{e~z^+}{4\pi~\varepsilon~(1+\chi~a)}~\frac{\exp[\chi~(a-r)]}{r}\]

D’où la d.d.p. \(V_N\) créé par le nuage : \[V_N=\frac{e~z^+}{4\pi~\varepsilon}~\frac{1}{r}~\Big\{\frac{\exp[\chi~(a-r)]}{1+\chi~a}-1\Big\}\]

On remarque que, à la place de l’ion, ce potentiel est le même que celui qui serait créé par une couche sphérique de charge (\(e~z^+\)) et de rayon \(l\) tel que : \[\frac{1}{l}=\frac{1}{a}~\Big\{\frac{1}{1+\chi~a}-1\Big\}=\frac{\chi}{1+\chi~a}\quad\Rightarrow\quad l=a+\frac{1}{\chi}\]

\(l\) représenterait le rayon du nuage.

Dans cette interaction, chaque ion (\(+\)) gagne une énergie potentielle, en commun avec les ions (\(-\)) : \[e~z^+~V_N(a)=\frac{e^2~(z^+)^2}{4\pi~\varepsilon~l}\]

Enfin, faisant l’hypothèse que \(\cfrac{1}{\chi}\gg a\) : \[l\approx\Big\{\frac{e^2}{\varepsilon~k~T}~\big[n_1~(z^+)^2+n_2~(z^-)^2\big]\Big\}^{-1/2}\]

Ou encore : \[l\approx~\sqrt{\frac{\varepsilon~k~T}{2~n~z^2~e^2}}\]