1. Sources ponctuelles

1.1. Équipotentielles et lignes de force

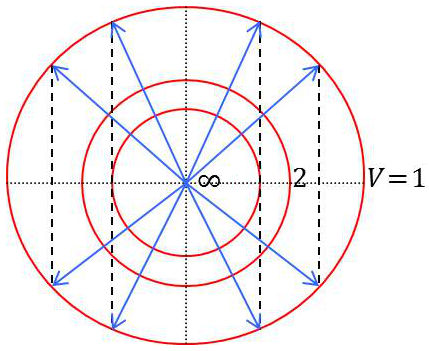Dans le cas d’une charge unique \(q\), on connaît, à une distance donnée \(r\), les expressions du potentiel et du champ électrique : \[\begin{aligned} V&=\frac{q}{4\pi~\varepsilon_0}~\frac{1}{r}\\ \overrightarrow{E}&=-\overrightarrow{\rm grad}(V)=\frac{q}{4\pi~\varepsilon_0}~\frac{\overrightarrow{r}}{r^3} \end{aligned} \qquad[1]\]

Les équipotentielles sont donc des sphères centrées sur \(q\) et les lignes de force les rayons de cette sphère.

La sphère de potentiel zéro est rejetée à l’infini. Le sens indiqué par les flèches correspond à une charge positive (il serait inversé dans le cas contraire).

Dans un système à \(n\) charges (différentes en valeur et en signe), on obtient pour \(V\) et pour \(E\) une résultante comme somme d’expressions précédentes. La recherche des équipotentielles et des lignes de force est ramenée à un problème de géométrie dans l’espace.

1.2. Perturbation d’un champ uniforme par une charge ponctuelle

Un champ uniforme peut être imaginé comme produit par une charge ponctuelle infiniment grande située à l’infini. Les lignes équipotentielles sont alors des parallèles équidistantes.

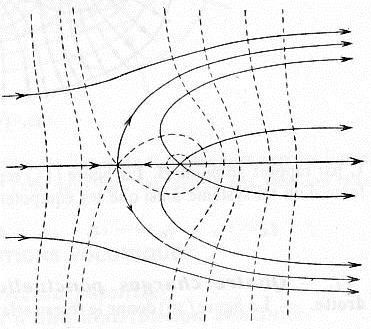En traçant les cercles dont les potentiels croissent régulièrement autour de la charge ponctuelle et finie introduite, on peut réunir d’un trait continu les points qui se trouvent sur une même surface équipotentielle du système. La figure ci-contre indique l’allure des courbes ainsi obtenues et les lignes de force qui leur sont orthogonales.

Ce système ne présente aucune surface équipotentielle ayant rigoureusement une forme géométrique simple. Cependant, autour de la charge, on voit que les surfaces équipotentielles peuvent, tout au moins en première approximation, être assimilées à des sphères.

C’est une solution approximative et acceptable pour l’influence de plusieurs sphères les unes sur les autres, à condition que les distances de leurs centres soient grandes par rapport aux rayons.

2. Distribution volumique

2.1. Continuités à la limite d’une distribution continue

Pour des raisons de simplicité, nous avons considéré des distributions discontinues \(\rho(x,~y,~z)\), constantes par exemple à l’intérieur d’un volume et nulles en dehors.

En fait, si \(\rho(x,~y,~z)\) est discontinu mais fini sur la surface, le potentiel et le champ ne subissent aucune discontinuité.

Reprenons pour cela deux formes intégrales précédentes (voir théorème de Gauss) : \[\begin{aligned} &\int_S(\overrightarrow{n}\wedge\overrightarrow{E})~ds=0\\ &\int_S(\overrightarrow{n}\cdot\overrightarrow{D})~ds=Q \end{aligned} \qquad[2]\]

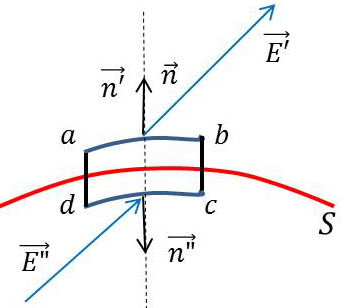
Appliquons ces relations à un petit cylindre dont les bases sont parallèles à la surface de séparation et dont la surface latérale est normale à la surface. On peut négliger cette surface latérale qui peut être rendue infiniment petite par rapport aux surfaces de base.

En notant que, le volume du cylindre tendant vers zéro, la charge totale finie qu’il contient tend aussi vers zéro, on obtient : \[\left\{ \begin{aligned} (\overrightarrow{D'}\cdot\overrightarrow{n'})+(\overrightarrow{D''}\cdot\overrightarrow{n''})&=0\\ (\overrightarrow{n'}\wedge\overrightarrow{E'})+(\overrightarrow{n''}\wedge\overrightarrow{E''})&=\overrightarrow{0} \end{aligned} \right. \qquad \text{ou} \qquad \left\{ \begin{aligned} D'_n&=D''_n\\ E'_t&=E''_t \end{aligned} \right. \qquad[3]\]

On notera que (vecteurs normaux unitaires) : \[\overrightarrow{n}=\overrightarrow{n'}=-\overrightarrow{n''}\]

Ainsi, les deux composantes (normale et tangentielle) du champ sont conservées à la transition de sorte que le champ est conservé : \[E'_n=E''_n~~~\text{et}~~~E'_t=E''_t\quad\Rightarrow\quad\overrightarrow{E'}=\overrightarrow{E''}\qquad[4]\]

Il s’ensuit par ailleurs que : \[\overrightarrow{n}\cdot\overrightarrow{\rm grad}(V')=\overrightarrow{n}\cdot\overrightarrow{\rm grad}(V'')\quad\Rightarrow\quad V'=V''\qquad[5]\]

Remarque

La condition \(V'=V''\) s’avère parfois utile pour fixer la constante du potentiel à l’intérieur d’un volume. Ceci est obtenu en deux temps : en la raccordant à la valeur extérieure qui elle-même se détermine par sa valeur nulle à l’infini.

2.2. Distribution uniforme à l’intérieur d’une sphère S

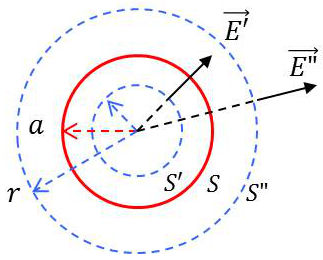Soit \(a\) le rayon de la sphère et \(\rho\) la densité de charge. La charge totale contenue dans la sphère est donc : \[Q=\frac{4\pi~a^2}{3}~\rho\qquad[5]\]

Les éléments de volume pouvant être associés de manière symétrique par rapport à un rayon donné, le vecteur champ électrique est porté par ce rayon.

Considérons à présent deux sphères \(S'\) et \(S''\) (virtuelles) concentriques avec \(S\) et de rayons respectifs \(r>a\) (pour \(S'\)) et \(r<a\) (pour \(S''\)).

Appliquons aux deux surfaces le théorème de Gauss :

1. \(S'\) surface extérieure à \(S\) : \[(4\pi~r^2)~\varepsilon_0~E'=Q\quad\Rightarrow\quad E'=\frac{Q}{4\pi~\varepsilon_0}~\frac{\overrightarrow{r}}{r^3}\qquad[6]\]

2. \(S''\) surface intérieure à \(S\) : \[(4\pi~r^2)~\varepsilon_0~E''=Q\quad\Rightarrow\quad E''=\frac{Q}{4\pi~\varepsilon_0}~\frac{\overrightarrow{r}}{a^3}\qquad[7]\]

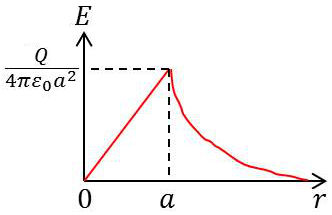Le champ à l’extérieur est donc le même que si toute la charge \(Q\) était réunie au centre ; le champ à l’intérieur varie linéairement de la valeur zéro au centre à la valeur : \[\frac{Q}{4\pi~\varepsilon_0}~\frac{1}{a^2}\qquad[8]\]

à la limite de la distribution.

D’où, par intégration, les expressions des potentiels : \[\begin{aligned} V'&=\frac{Q}{4\pi~\varepsilon_0}~\frac{1}{r}+k_1\\ V''&=-\frac{1}{2}~\frac{Q}{4\pi~\varepsilon_0}~\frac{r^2}{a^3}+k_2 \end{aligned} \qquad[9]\]

Les constantes sont obtenues par les conditions aux limites : \[V'_{r=\infty}=0\qquad;\qquad V'_{r=a}=V''_{r=a}\]

Tous calculs faits : \[\begin{aligned} V'&=\frac{Q}{4\pi~\varepsilon_0}~\frac{1}{r}\\ V''&=\frac{Q}{8\pi~\varepsilon_0}~\Big\{\frac{3}{a}-\frac{r^2}{a^3}\Big\} \end{aligned} \qquad[10]\]

2.3. Distribution quelconque de charges simples

On considère le cas tridimensionnel d’une distribution quelconque de charges simples en coordonnées cartésiennes.

Soit \(\rho(u,~v,~w)\) la densité de charge électrique à l’intérieur d’un volume limité. Le potentiel au point \(P(x,~y,~z)\) est : \[V=\frac{1}{4\pi~\varepsilon_0}\int_V\frac{\rho(u,~v,~w)}{r}~d\tau\qquad[11]\]

avec : \[d\tau=du~dv~dw\quad;\quad r=\sqrt{(x-u)^2+(y-v)^2+(z-w)^2}\]

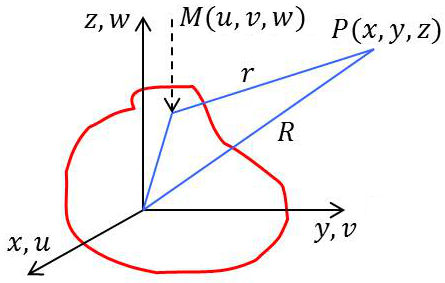Choisissons l’origine \(O\) quelque part à l’intérieur de la distribution. Toutes les charges sont supposées à l’intérieur d’une sphère de rayon \(R_0\) (rayon maximal).

Si l’on s’en tient au calcul du potentiel à l’extérieur de cette sphère et si la distance \(r\) qui est une fonction de \(u,~v,~w\) (assez grande), on pourra développer le terme \(1/r\) en série de Taylor. Il suffit pour cela de prendre les dérivées de \(r\) par rapport à \(u,~v,~w\), puis de faire \(u,~v,~w=0\) dans le résultat obtenu.

3. Distributions superficielles

3.1. Champ et potentiel au voisinage d’une couche simple

3.1.1. Champ

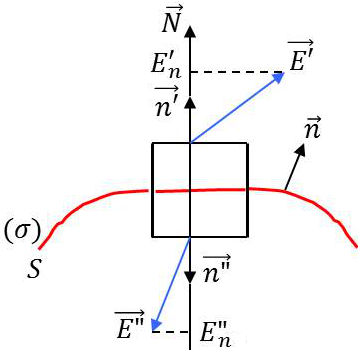Considérons une surface \(S\) portant une densité de charge \(\rho\). Au voisinage du point \(M\), on peut imaginer un petit cylindre élémentaire dont les bases sont parallèles à la surface et de chaque côté de celle-ci.

On pourra ensuite diminuer indéfiniment la hauteur de telle sorte que la surface latérale soit négligeable par rapport à la surface des bases.

Appliquons le théorème de Gauss à ce cylindre : \[(\overrightarrow{D'}\cdot\overrightarrow{n'})~ds+(\overrightarrow{D''}\cdot\overrightarrow{n''})~ds=0\qquad[12]\]

Mais on sait que : \[\overrightarrow{n}=\overrightarrow{n'}=-\overrightarrow{n''}\]

On aura donc : \[\begin{aligned} &\overrightarrow{n}\cdot(\overrightarrow{D'}-\overrightarrow{D''})=\sigma\qquad\text{ou}\qquad D'_n-D''_n=\sigma\\ &\overrightarrow{D}=\varepsilon_0\overrightarrow{E}\qquad\Rightarrow\qquad E'_n-E''_n=\frac{\sigma}{\varepsilon_0} \end{aligned} \qquad[13]\]

Ainsi, à la traversée d’une couche simple de charges électriques, la composante normale de l’induction électrique subit une discontinuité égale à \(\sigma\).

Inversement, si l’induction électrique subit une discontinuité à la traversée d’une surface, on peut affirmer que celle-ci porte une densité de charge égale à \(\sigma\).

En appliquant maintenant la deuxième équation sous sa forme intégrale au cylindre élémentaire précédent, on obtient : \[(\overrightarrow{n'}\wedge\overrightarrow{E'})~ds+(\overrightarrow{n''}\wedge\overrightarrow{E''})~ds=0\qquad[14]\]

et, compte tenu des relations aux normales : \[\overrightarrow{n}\wedge(\overrightarrow{E'}-\overrightarrow{E''})=0\qquad\Rightarrow\qquad E'_t=E''_t\qquad[15]\]

Ces dernières relations montrent que les composantes tangentielles du champ varient de manière continue à la traversée de la surface.

3.1.2. Potentiel

Pour le calcul du potentiel, nous écrivons d’une manière générale : \[V(x,~y,~z)=\int_S\frac{\sigma~ds}{r}\qquad[16]\]

Considérons le point \(M(x,~y,~z)\) sur la surface et traçons un cercle avec ce point pour centre. On suppose le rayon suffisamment petit pour que la surface se confonde avec cette partie du plan tangent.

Le potentiel au point \(M\) comprend une partie \(V_1\) due aux charges en dehors du cercle et une partie \(V_2\) due aux charges à l’intérieur du cercle.

Pour cette dernière partie, supposons que \(\sigma\) soit fini. On peut alors trouver un nombre \(k\) tel que : \[|\sigma|~<~k\qquad\Rightarrow\qquad \Big|\frac{\sigma}{r}\Big|~<~\frac{k}{r}\qquad[17]\]

Par suite : \[V_2~<~k~\int_S\frac{ds}{r}=2\pi~k~a\qquad[18]\]

Ainsi, quand \(a\rightarrow0\), il vient \(V_2\rightarrow 0\), c’est-à-dire que \(V=V_1\), car c’est est une fonction continue au point considéré.

3.2. Champ sur une surface

D’après le théorème de Gauss, le flux envoyé par une charge ponctuelle placée sur une surface à travers cette surface même est égal à \(q/2\).

Nous exploiterons ce résultat pour calculer la valeur du champ \(E\) sur la surface même. On opère d’abord avec un cylindre dont une base est sur la surface et l’autre au voisinage immédiat extérieur.

Revenant à la relation de Gauss : \[\int_S(\overrightarrow{n}\cdot\overrightarrow{D})~ds=\frac{Q}{2}\qquad[19]\]

Il vient : \[E'_n-E_n=\frac{\sigma}{2\varepsilon_0}\qquad[20]\]

En opérant de même avec un cylindre dont l’une des bases est sur la surface et l’autre au voisinage immédiat intérieur, on aurait : \[E_n-E''_n=\frac{\sigma}{2~\varepsilon_0}\qquad[21]\]

En retranchant membre à membre ces deux équations : \[2~E_n=E'_n+E''_n\qquad[22]\]

Comme les composantes tangentielles sont continues, \(E'_t=E''_t\), on en conclut que : \[\overrightarrow{E}=\frac{1}{2}~(\overrightarrow{E'}+\overrightarrow{E''})\qquad[23]\]

3.3. Disque circulaire uniformément chargé

3.3.1. Potentiel et champ en un point de l’axe

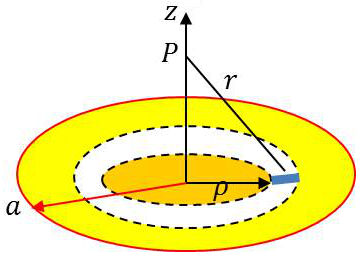Soit \(\sigma\) la densité superficielle de charge.

Le potentiel en un point \(P\) de l’axe du disque est : \[V=\frac{\sigma}{4\pi~\varepsilon_0}\int_S\frac{ds}{r}=\frac{\sigma}{2~\varepsilon_0}\int_{\rho=0}^{\rho=a}\frac{\rho~d\rho}{\sqrt{\rho^2+z^2}}\qquad[24]\]

Et en intégrant : \[V=\frac{\sigma}{2~\varepsilon_0}~\Big[\sqrt{\rho^2+z^2}\Big]_{\rho=0}^{\rho=a}=\frac{\sigma}{2~\varepsilon_0}~\Big[\sqrt{[a^2+z^2]}-|z|\Big]\qquad[25]\]

les conditions aux limites étant (\(z=0~,~z=\infty\)).

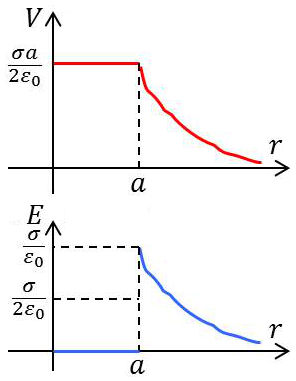
— Au centre : \[z=0\qquad;\qquad V_0=\frac{\sigma~a}{2~\varepsilon_0}\]

— À l’infini (résultat immédiat sans intégration) : \[z=\infty\qquad;\qquad V_0=\infty\]

Pour obtenir le champ au point \(P\), il suffit de remarquer que le champ est dirigé vers l’axe des \(z\) en vertu de la symétrie du système. On a donc : \[E=E_z=-\frac{\partial V}{\partial z}=-\frac{\sigma}{2~\varepsilon_0}~\Big\{\frac{z}{\sqrt{z^2+a^2}}-(\pm 1)\Big\}\qquad[25]\]

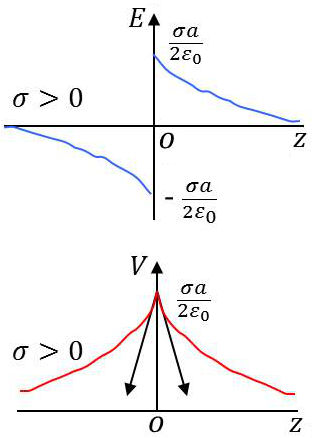Étudions succinctement la forme des courbes :

Conditions aux limites :

\[\begin{aligned} &z\rightarrow 0^+ && E_0\rightarrow \frac{\sigma}{2~\varepsilon_0}\\ &z\rightarrow 0^- && E_0\rightarrow -\frac{\sigma}{2~\varepsilon_0}\\ &z\rightarrow\pm\infty && E_{\infty}\rightarrow 0\end{aligned}\]

Conformément à la formule générale : \[E'_n-E''_n=\frac{\sigma}{\varepsilon_0}\]

Le champ subit une discontinuité \(\sigma/\varepsilon_0\) à la traversée de la couche tandis que le potentiel varie d’une manière continue.

À grande distance : \[V\cong \frac{\sigma~a^2}{4~\varepsilon_0}~\frac{1}{z}=\frac{Q}{4\pi~\varepsilon_0}~\frac{1}{z}\qquad[26]\]

Le potentiel est le même que si une charge ponctuelle égale à la charge totale du disque était placée à l’origine.

3.3.2. Potentiel et champ en dehors de l’axe

En dehors de l’axe, le calcul direct par l’intégrale du potentiel coulombien ne se présente pas de manière simple. Cependant, pour des systèmes de révolution, le potentiel hors de l’axe se déduit de plusieurs manières du potentiel sur l’axe.

Il est également possible d’utiliser des développements en série comme les polynômes de Legendre et une intégrale portant sur la fonction de Bessel.

3.4. Plan infini uniformément chargé

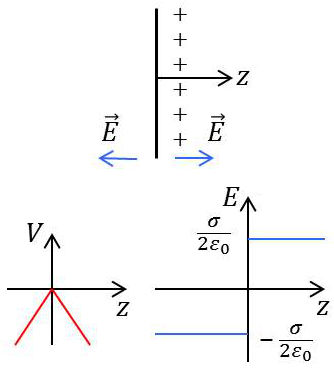On peut considérer le plan infini comme le cas limite du disque dont le rayon \(a\) prendrait une valeur infinie.

Dans ce cas, la fonction potentiel ne peut être utilisée, car on obtient une valeur infinie. En revanche, il est possible d’utiliser l’expression du champ qui a une valeur finie, c’est-à-dire : \[a\rightarrow\infty\qquad\text{alors :}\quad E_z=\pm\frac{\sigma}{2\varepsilon_0}\qquad[27]\]

On obtient alors l’expression du potentiel par intégration : \[V=-\frac{\sigma}{2~\varepsilon_0}~|z|+\text{cte}\qquad[28]\]

Les variations du champ et du potentiel sont représentées graphiquement ci-contre. On a supposé que \(\sigma>0\) et que la constante du potentiel est égale à zéro.

3.5. Deux plans parallèles avec des charges de signes contraires

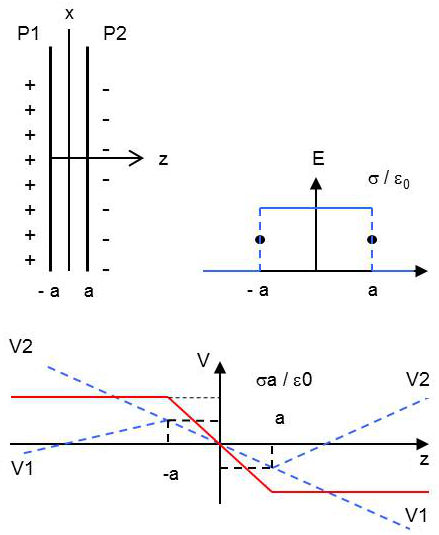Dans le cas de deux plans parallèles avec des charges de signes contraires, il suffit de superposer des solutions analogues à celles du paragraphe précédent :

1. plan \(P1\) seul et en abscisse (\(-a\)) : on retrouve la solution dans laquelle \(z =-a\) ;

2. plan \(P_2\) seul et en abscisse (\(+a\)) : on retrouve la solution dans laquelle \(z =+a\).

On obtient ensuite \(E\) par intégration du potentiel :

• la partie \(V=cte\) du potentiel entraîne \(E =0\) ;

• la partie variation linéaire entraîne \(E=cte\).

On notera la présence des deux discontinuités aux points d’abscisse (\(-a\)) et (\(+a\)).

En résumé, pour le champ et le potentiel :

\[\begin{aligned} E=E_1+E_2&= \left\{ \begin{aligned} &0\\ &\frac{\sigma}{\varepsilon_0}\\ &0 \end{aligned} \right. \qquad[28] \\ V=V_1+V_2&= \left\{ \begin{aligned} +\frac{\sigma~a}{\varepsilon_0}\\ -\frac{\sigma~z}{\varepsilon_0}\\ -\frac{\sigma~a}{\varepsilon_0} \end{aligned} \right. \qquad \text{quand :} \quad \begin{aligned} z&<-a\\ -a&<z<a\\ a&<z \end{aligned} \qquad[29]\end{aligned}\]

3.6. Couche sphérique uniforme

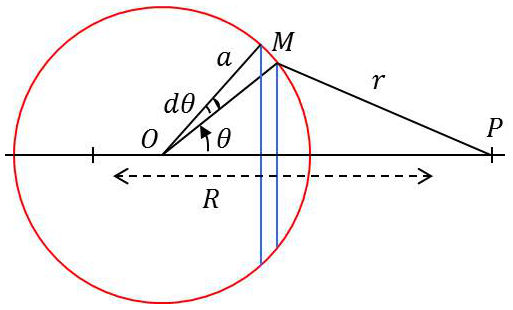Soit \(\sigma\) la densité superficielle de charge et \(a\) le rayon de la sphère. La charge totale est donc : \[Q=4\pi~a^2~\sigma\qquad[30]\]

On calcule le potentiel par la formule : \[V=\frac{\sigma}{4\pi~\varepsilon_0}~\int_S \frac{ds}{r}\qquad[31]\]

En combinant l’expression de l’élément de surface : \[ds=2\pi~a~\sin\theta~a~d\theta\]

et la différentielle de l’expression : \[r^2=R^2+a^2-2~a~R~\cos\theta\]

on obtient pour le potentiel : \[V=\frac{1}{4\pi~\varepsilon_0}~\frac{Q}{2~a~R}~\int dr\qquad[32]\]

– Point \(P\) extérieur : intégration de \([R-a]\) à \([R+a]\) ;

– Point \(P\) intérieur : intégration de \([a-R]\) à \([R+a]\).

On obtient respectivement : \[V'=\frac{1}{4\pi~\varepsilon_0}~\frac{Q}{R}\quad;\quad V''=\frac{1}{4\pi~\varepsilon_0}~\frac{Q}{a}\qquad[33]\]

Pour les champs, on applique la relation : \[E=\frac{\partial V}{\partial r}\]

Ce qui conduit à : \[E'=\frac{1}{4\pi~\varepsilon_0}~\frac{Q}{R^2}\quad;\quad E''=0\qquad[34]\]

Le champ est nul à l’intérieur et, à l’extérieur, il est le même que si toute la charge était réunie au centre de la sphère.

On aurait d’ailleurs pu obtenir ces résultats en appliquant le théorème de Gauss à deux sphères concentriques de la première, l’une intérieure et l’autre extérieur (flux du vecteur \(D\)).

3.7. Couche cylindrique uniforme

On désigne par \(a\) le rayon de la section droite du cylindre et par \(\sigma\) la densité superficielle. On considère la charge totale \(Q\) portée par unité de longueur, soit \(Q=2\pi~a~\sigma\). Par raison de symétrie, le champ est dirigé suivant le rayon de la section droite.

En appliquant le théorème de Gauss à deux cylindres coaxiaux de rayon \(r\), l’un intérieur et l’autre extérieur au cylindre chargé de rayon \(a\), on obtient : \[E'=\frac{Q}{2\pi~\varepsilon_0}~\frac{1}{r}\quad;\quad E''=0\qquad[35]\]

On en déduit les potentiels par intégration (\(E=-\partial V/\partial r\)) : \[V'=\frac{Q}{2\pi~\varepsilon_0}~\ln(r)+k_1\quad;\quad V''=k_2\qquad[36]\]

Pour déterminer les constantes, il faut choisir une origine des potentiels et écrire que le potentiel est continu à la traversée de la couche.

En choisissant \(r=1\), donc\(V=0\), il vient : \[k_1=0\quad;\quad k_2=-\frac{Q}{2\pi~\varepsilon_0}\ln(a)\]

Par suite : \[V'=-\frac{Q}{2\pi~\varepsilon_0}~\ln(r)\quad;\quad V''=-\frac{Q}{2\pi~\varepsilon_0}~\ln(a)\]

4. Distributions linéaires

4.1. Droite indéfinie uniformément chargée

On désigne par \(\lambda\) la densité linéaire de charge. Pour calculer le champ \(E\) à une distance donnée \(R\) de la ligne, nous remarquerons que, pour des raisons de symétrie, ce vecteur (radial) sera perpendiculaire à la ligne.

Appliquons le théorème de Gauss à une surface cylindrique de rayon \(R\) et hauteur unitaire entourant la ligne. Pour le champ (à partir du vecteur induction) : \[(\varepsilon_0~E)~(2\pi~R)=\lambda\quad\Rightarrow\quad E=\frac{\lambda}{2\pi~\varepsilon_0}~\frac{1}{R}\qquad[37]\]

D’où le potentiel (intégration) : \[V=-\frac{\lambda}{2\pi~\varepsilon_0}~\ln(R)\qquad[38]\]

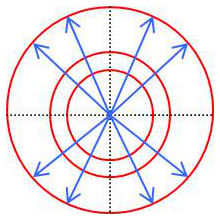La figure ci-contre représente la trace des surfaces équipotentielles qui sont des cylindres coaxiaux. Cette figure est à comparer avec celle obtenue dans le cas d’une charge ponctuelle.

Ici en particulier, les plans équiflux passant par la droite sont répartis d’une manière angulaire uniforme.

La constante liée à l’intégration de \(E\) a pour valeur zéro, car on a fixé le potentiel de référence à zéro pour une distance \(R=1\).

4.2. Deux droites infinies avec des charges égales et opposées

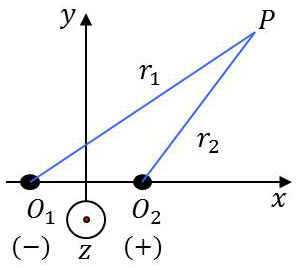Les densités linéaires sont supposées uniformes : \[\lambda=-\lambda_1=\lambda_2\qquad[39]\]

Le potentiel V est la somme des deux potentiels : \[V=V_1+V_2=\frac{\lambda}{2\pi~\varepsilon_0}~\ln\frac{r_1}{r_2}\qquad[40]\]

C’est-à-dire : \[\frac{r_1}{r_2}=\exp\Big(\frac{2\pi~\varepsilon_0}{\lambda}\Big)\qquad[41]\]

D’où ce résultat remarquable que toutes les surfaces équipotentielles sont des cylindres circulaires. Leur section droite est le lieu des points dont les rapports des distances à deux points fixes est constant. C’est donc une circonférence ayant son centre sur l’axe \(Ox\).

Les lignes de force forment aussi une famille de cercles orthogonaux aux précédents ayant leurs centres sur l’axe \(Oy\). Ce résultat peut être obtenu de manière très simple en utilisant les transformations conformes.

4.3. Spire circulaire uniformément chargée

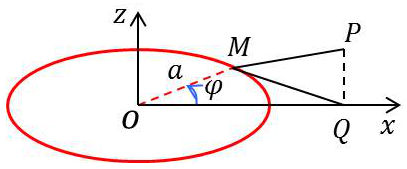Soit \(\lambda\) la densité linéaire de charge : \[V=\frac{\lambda}{4\pi~\varepsilon_0}~\int_C\frac{dl}{r}\qquad[42]\]

Le système étant de révolution, il suffit de calculer \(V\) dans le plan \(xOz\).

En désignant par \(R=\overline{OQ}\) la distance du point \(P\) à l’axe de révolution : \[r=\sqrt{z^2+{\overline{MQ}}^2}=\sqrt{z^2+a^2+R^2-2~a~R~\cos\varphi}\]

Le calcul est relativement complexe ; il conduit à l’expression suivante : \[V(z,R)=\frac{\lambda}{\pi~\varepsilon_0}~\frac{1}{(z/a)^2+(1+R/a)^2}~J_1\qquad[43]\]

\(J_1\) désignant l’intégrale de Legendre de première espèce : \[J_1=\int_0^{2\pi}\frac{d\psi}{\sqrt{1-k^2~\sin^2\psi}}\qquad\text{avec :}\quad k^2=\frac{4~a~R}{z^2+(a+R)^2}\qquad[44]\]

Un cas particulier intéressant est celui de l’axe de la spire : \[R=0\quad;\quad J_1(0)=\frac{\pi}{2}\qquad\Rightarrow\qquad V(z,~0)=\frac{\lambda}{2~\varepsilon_0}~\frac{1}{\sqrt{1+(z/a)^2}}\qquad[45]\]

Ce qui était d’ailleurs évident sans calcul.