1. Influence d’une charge (ou ligne) uniformément chargée sur un conducteur
1.1. Plan conducteur réuni au sol (potentiel zéro)
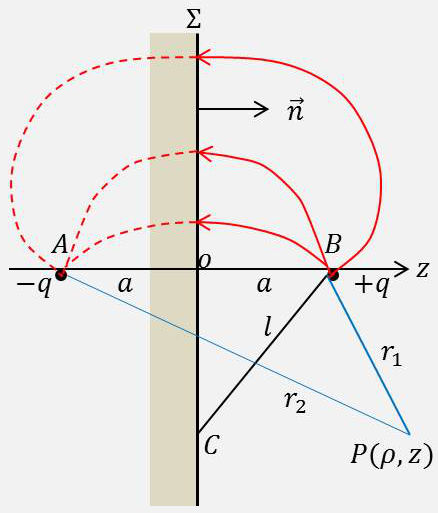 Nous avons remarqué que l’équipotentielle zéro de deux charges égales et de signes contraires était le plan normal au milieu du segment qui joint les deux charges.
Nous avons remarqué que l’équipotentielle zéro de deux charges égales et de signes contraires était le plan normal au milieu du segment qui joint les deux charges.
On peut donc remplacer ce plan par un véritable conducteur au potentiel zéro sans modifier le champ et le potentiel dans la région des \(z\) positifs.
Ce potentiel donnera donc la solution du problème de l’influence d’une charge ponctuelle sur un plan, soit : \[\begin{aligned} &V=\frac{q}{4\pi~\varepsilon_0}~\Big(\frac{1}{r_1}-\frac{1}{r_2}\Big)\\ &r_1=\sqrt{\rho^2+(z-a)^2}\quad;\quad r_2=\sqrt{\rho^2+(z+a)^2} \end{aligned} \qquad[1]\]
La densité de charge qui apparaissent sur le plan par influence est : \[\sigma=-\varepsilon_0~\Big(\frac{\partial V}{\partial z}\Big)_{z=0}=-\frac{a~q}{2\pi~(\rho^2+a^2)^{3/2}}=-\frac{a~q}{2\pi~l^3}\qquad[2]\]
À gauche du plan (région des \(z\) négatifs), le potentiel est partout nul, ainsi que le champ. Si ce champ est nul, c’est parce que les charges négatives qui apparaissent par influence créent à gauche un champ égal et opposé au champ de la charge \((+q)\) placée en \(B\). On peut dire que le plan joue le rôle d’un écran pour le champ de cette dernière charge.
La première formule ne donne le potentiel qu’à droite du plan. Pour avoir l’expression du potentiel valable partout, il faut écrire : \[V=V_0-2~\varepsilon_0\int_S\frac{\partial V_0}{\partial z}~\frac{dS}{dr}\qquad[3]\]
-
\(V_0\) est le potentiel de la charge \((+q)\).
-
L’intégrale représente le potentiel des charges qui apparaissent par influence.
-
\(r\) est la distance de l’élément \(dS\) au point où l’on calcul le potentiel.
Remarque
On étudierait de la même manière l’influence d’une ligne indéfinie uniformément chargée sur un plan conducteur au potentiel zéro, le potentiel logarithmique remplaçant le potentiel coulombien.
1.2. Charge entre deux plans parallèles réunis au sol (potentiel zéro)
La solution du problème d’une charge entre deux plans parallèles réunis au sol oblige à considérer une infinité d’images qui rappellent les réflexions multiples sur deux miroirs parallèles.
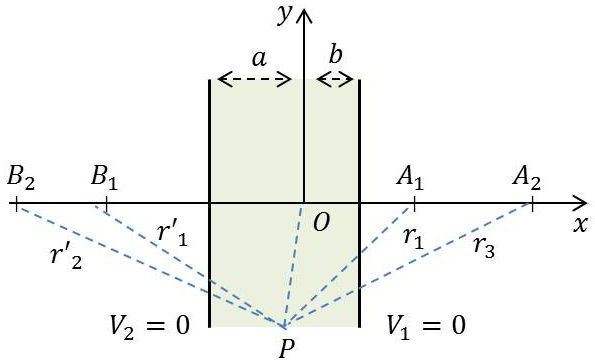 La charge \((+q)\) placée en \(O\) donne une image en \(A_1\), symétrique de \(O\) par rapport au premier plan, puis cette image \(A_1\) donne une image \(B_2\) symétrique de \(A_1\) par rapport au deuxième plan et ainsi de suite.
La charge \((+q)\) placée en \(O\) donne une image en \(A_1\), symétrique de \(O\) par rapport au premier plan, puis cette image \(A_1\) donne une image \(B_2\) symétrique de \(A_1\) par rapport au deuxième plan et ainsi de suite.
Dans la région comprise entre les deux plans les potentiels produits par les différentes images vont en diminuant.
En fin de compte, il y a symétrie des effets par rapport à chacun des plans, d’où : \[V_1=V_2=0\]
En un point \(P\), le potentiel est celui qui est produit par la charge \(q\) placée en \(O\) et par l’ensemble des images, soit : \[V_P=\frac{1}{4\pi~\varepsilon_0}~\Big\{\frac{q}{r_0}+\sum_{i=1}^{i=\infty}q_i~\Big(\frac{1}{r_1}+\frac{1}{r'_i}\Big)\Big\}\quad;\quad q_i=\pm~q\qquad[3]\]
Si \(a=b=c\) , le potentiel produit par les images à l’origine \(O\) a pour expression : \[V_0=\frac{q}{4\pi~\varepsilon_0}~2\sum_{i=1}^{i=\infty}\frac{(-1)^i}{2~c~i}=-\frac{q}{4\pi~\varepsilon_0}~\ln(2)\qquad[4]\]
Si on a une petite sphère de centre \(O\) et de rayon \(R \ll c\), on peut admettre que le potentiel produit par les images est sensiblement la même sur toute la sphère, d’où la solution du problème d’une petite sphère portée à un potentiel constant entre deux plans reliés au sol : \[V_0=\frac{q}{4\pi~\varepsilon_0}~\Big\{\frac{1}{R}-\frac{\ln(2)}{c}\Big\}\qquad[5]\]
Si l’on avait une ligne chargée entre deux plans, la position des images serait la même et le potentiel en \(P\) serait : \[V_P=-\frac{1}{2\pi~\varepsilon_0}~\Big\{\lambda~\ln(r_0)+\sum_{i_1}^{i=\infty}\lambda_i~\big[\ln(r_i~r'_i)\big]\Big\}\qquad[6]\]
1.3. Calcul de la charge totale qui apparaît par influence
1.3.1. Un seul conducteur en présence de la charge
En appliquant l’identité de Gauss aux deux états d’équilibre : \[\{q,~Q~~;~~V_P,~0\}\quad\text{et}\quad\{0,~Q'~~;~~V'_P,~V'\}\qquad[7]\]
On obtient : \[q~V'_P+Q~V'=0\quad\Rightarrow\quad Q=-\frac{V'_P}{V'}~q\qquad[8]\]
On peut donc calculer \(Q\) qui apparaît sur le conducteur réuni au sol si on sait quel est le potentiel \(V'_P\) produit au point \(P\), la charge \(q\) étant absente, par le conducteur porté au potentiel \(V'\).
On notera que \(V_P\) qui est infini ne figure pas dans la formule finale \((0~V_P=0)\).
Exemple
Charge ponctuelle à une distance D du centre d’une sphère conductrice de rayon \(a\) reliée au sol. On a alors : \[V'_P=\frac{a}{D}~V'\quad\Rightarrow\quad Q=-\frac{a}{a}~q\qquad[9]\]
1.3.2. Charge ponctuelle entre deux conducteurs, l’un entourant totalement l’autre
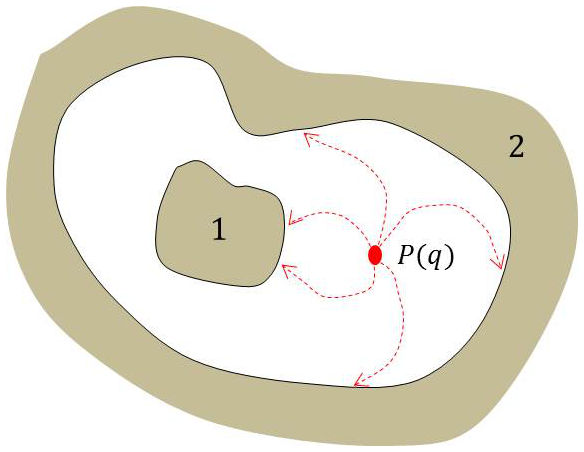 En appliquant l’identité de Gauss aux deux états d’équilibre : \[\begin{aligned} \{q,~Q_1,~Q_2~~&;~~V_P,~0,~0\}\\ \{0,~Q'_1,~Q'_2~~&;~~V'_P,~V'_1,~V'_2\} \end{aligned} \qquad[14]\]
En appliquant l’identité de Gauss aux deux états d’équilibre : \[\begin{aligned} \{q,~Q_1,~Q_2~~&;~~V_P,~0,~0\}\\ \{0,~Q'_1,~Q'_2~~&;~~V'_P,~V'_1,~V'_2\} \end{aligned} \qquad[14]\]
On obtient : \[q~V'_P+Q_1~V'_1+Q_2~V'_2=0\qquad[11]\]
Comme tous les tubes de force qui partent de \(P\) aboutissent sur les surfaces des deux conducteurs, on a, d’après le théorème des états correspondants : \[Q_1+Q_2=-q\qquad[12]\]
Et il vient : \[Q_1=-\frac{V'_P-V'_2}{V'_1-V'_2}~q\quad;\quad Q_2=-\frac{V'_P-V'_1}{V'_2-V'_1}~q\qquad[13]\]
Exemple : Charge ponctuelle entre deux plans
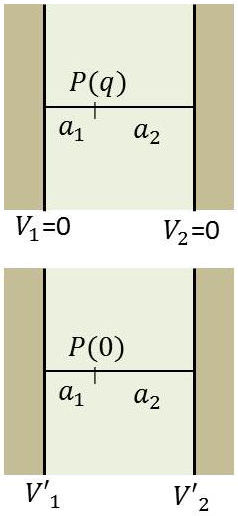 En l’absence de la charge ponctuelle, nous savons que le potentiel varie linéairement entre les deux plans d’où : \[\begin{aligned} &\frac{V'_P-V'_2}{V'_1-V'_2}=\frac{a_2}{a_1+a_2}\\ &\frac{V'_P-V'_1}{V'_2-V'_1}=\frac{a_1}{a_1+a_2} \end{aligned} \qquad[14]\]
En l’absence de la charge ponctuelle, nous savons que le potentiel varie linéairement entre les deux plans d’où : \[\begin{aligned} &\frac{V'_P-V'_2}{V'_1-V'_2}=\frac{a_2}{a_1+a_2}\\ &\frac{V'_P-V'_1}{V'_2-V'_1}=\frac{a_1}{a_1+a_2} \end{aligned} \qquad[14]\]
Ce qui donne les charges induites par influence sur chacun des deux plans : \[\begin{aligned} &Q_1=-\frac{a_2}{a_1+a_2}~q\\ &Q_2=-\frac{a_1}{a_1+a_2}~q \end{aligned} \qquad[15]\]
On traiterait de la même manière l’influence d’une charge entre les deux armatures d’un condensateur calculable, par exemple sphérique ou cylindrique.
2. Influence d’un champ donné sur un conducteur
Si le champ \(\overrightarrow{E_0}\) est donné, on connaît évidemment ses sources, c’est-à-dire les distributions qui le produisent. Dans ces conditions, on voit que si l’on connaît l’influence d’une charge ponctuelle (ou d’une ligne) sur le conducteur considéré, on aura la solution qui nous intéresse ici par une intégrale étendue aux volumes ou aux surfaces sur lesquelles se trouvent les charges qui produisent ce champ.
En général, cette intégrale peut être compliquée et ce n’est pas elle que nous utiliserons dans ce qui suit. Quand les conducteurs ont des formes simples, nous allons voir qu’il existe des formules donnant la solution sans aucun calcul.
Il faut noter qu’au point de vue expérimental, il n’est pas toujours facile de disposer d’un champ \(\overrightarrow{E_0}\) donné qui reste fixe. Si par exemple les charges qui produisent \(\overrightarrow{E_0}\) se trouvent sur des conducteurs voisins des conducteurs influencés, ces derniers réagiront sur la distribution des charges d’influence et ne sera plus constant. Cependant, si les conducteurs sont assez éloignés ou si les charges d’influence sont fixées rigidement sur des diélectriques, on aura un champ qui sera pratiquement constant.
2.1. Sphère dans un champ uniforme
Nous avons vu qu’en superposant un champ constant : \[E_x=E_y=0\quad;\quad E_z=E\qquad[16]\]
au champ d’un dipôle élémentaire placé à l’origine et orienté suivant les \(z\) positifs, l’équipotentielle zéro du champ résultant était une sphère. Le potentiel résultant de la superposition des deux champs s’écrit : \[V=\frac{p}{4\pi~\varepsilon_0}~\frac{\cos\theta}{r}-E~r~\cos\theta\qquad[17]\]
Soit \(a\) le rayon de notre sphère.
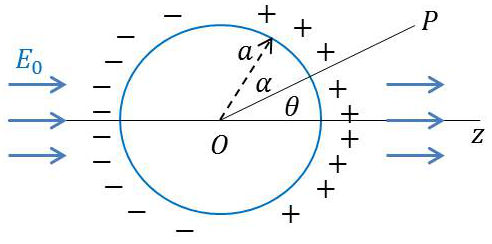 Pour que \(V=0\) quand \(r=a\), il faut que : \[p=4\pi~\varepsilon_0~a^2~E\qquad[17]\]
Pour que \(V=0\) quand \(r=a\), il faut que : \[p=4\pi~\varepsilon_0~a^2~E\qquad[17]\]
D’où la solution : \[V=\Big(\frac{a^2}{r^2}-r\Big)~E~\cos\theta\qquad[18]\]
Ce potentiel est bien celui qui convient, car il obéit partout à l’équation de Laplace en dehors de la sphère.
Sa seule singularité est à l’origine. À grande distance, le potentiel des charges qui apparaissent par influence sur la sphère tend vers zéro et il doit bien rester le potentiel de champ influençant.
La densité de charge sur la sphère est donnée par : \[\sigma=-\varepsilon_0~\Big(\frac{\partial V}{\partial r}\Big)_{r=a}=3~\varepsilon_0~E~\cos\theta\qquad[19]\]
2.2. Influence sur un plan au potentiel zéro
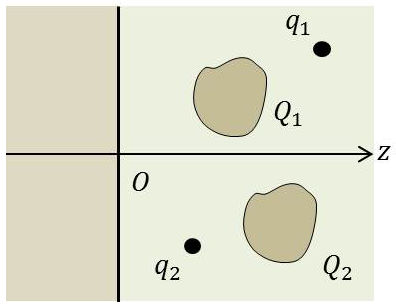 Le plan influencé est normal à l’axe \(Oz\) et passe par l’origine comme l’indique la figure. Toutes les charges du plan influençant se trouvent à droite du plan, c’est-à-dire dans la région \(z>0\).
Le plan influencé est normal à l’axe \(Oz\) et passe par l’origine comme l’indique la figure. Toutes les charges du plan influençant se trouvent à droite du plan, c’est-à-dire dans la région \(z>0\).
Soit \(f(x,~y,~z)\) le potentiel du champ influençant ; le potentiel cherché pour \(z>0\) est : \[V=f(x,~y,~z)-f(x,~y,~-z)\qquad[20]\]
En effet, si \(f(x,~y,~z)\) satisfait à l’équation de Laplace, il en est de même pour la fonction \(f(x,~y,~-z)\) et quand \(z=0\), c’est-à-dire sur le plan, on a bien \(V=0\).
De plus, les sources de \(f(x,~y,~z)\) étant toutes à droite du plan, les sources de \(f(x,~y,~-z)\) sont toutes à gauche du plan, c’est-à-dire dans une région qui est exclue du domaine considéré.
La densité de charge qui apparaît par influence sur le plan est : \[\sigma=-\varepsilon_0~\Big(\frac{\partial V}{\partial z}\Big)_{z=0}=-2~\varepsilon_0~f'(x,~y,~0)\qquad[21]\]
Pour en revenir à l’expression de \(V\), nous remarquerons que l’influence d’une charge ponctuelle sur un plan que nous avons déjà étudiée, plus particulièrement la formule en tout début de chapitre, n’est qu’un cas particulier de cette expression de \(V\).
2.3. Phénomènes généraux d’influence
Quand on frotte un bâton de verre ou de résine sur une étoffe de laine, ils sont capables d’attirer les corps légers. Ces corps se chargent d’électricité positive ou négative par le frottement. S’ils attirent d’autres corps, c’est à cause des charges par influence qu’ils y développent.
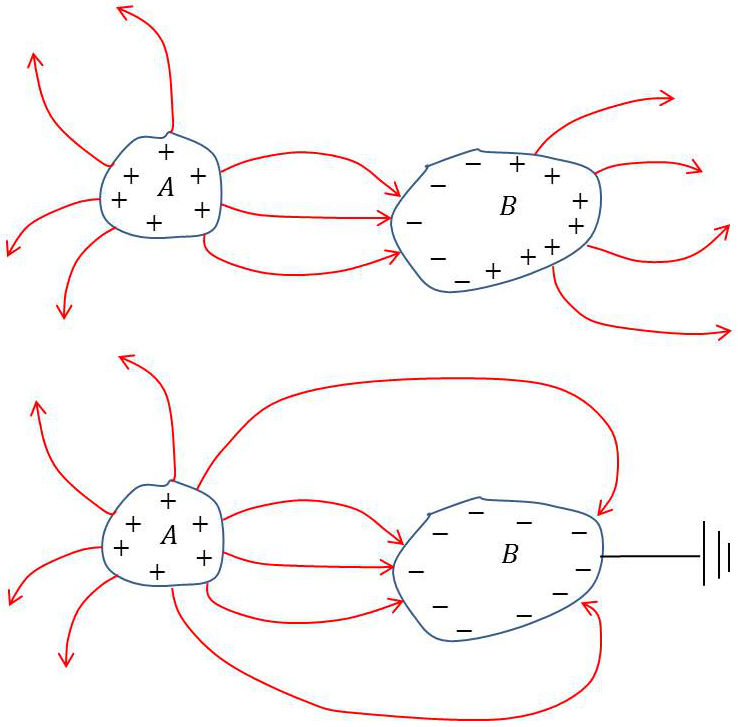 Si le conducteur influencé \(B\) est isolé, il apparaît autant de charges \((+)\) que de charges \((-)\). Il existe une ligne neutre qui sépare les régions chargées positivement de celles qui sont chargées négativement.
Si le conducteur influencé \(B\) est isolé, il apparaît autant de charges \((+)\) que de charges \((-)\). Il existe une ligne neutre qui sépare les régions chargées positivement de celles qui sont chargées négativement.
La région qui est la plus proche du corps influençant est chargée de signe contraire et cette charge est toujours plus petite en valeur absolue que celle du corps influençant. En effet, certaines des lignes de force qui partent de ce dernier n’aboutissent pas sur le corps influencé comme le montre la première figure.
Si le corps influencé est relié au sol, il ne porte que des charges de signe contraire à celles du corps influençant et leur valeur absolue est toujours plus petite que celle de \(A\).
Ainsi, l’électroscope à feuille d’or (ou d’aluminium) est un dispositif très sensible aux phénomènes d’influence. Si les feuilles d’or sont électrisées, elles se repoussent.
3. Système de plusieurs conducteurs
Le calcul des coefficients \(p_{ij}\) est en général un problème très difficile et la formule de définition n’est d’aucune utilité, car on ne connaît pas les densités sur les conducteurs.
Quand les distances \(r\) entre les conducteurs sont grandes par rapport aux dimensions des conducteurs eux-mêmes, on peut utiliser des formules approchées. Par exemple, avec deux conducteurs, on peut prendre comme approximation : \[p_{11}=\frac{1}{C_1}\quad;\quad p_{12}=p_{21}=\frac{1}{4\pi~\varepsilon_0~r}\quad;\quad p_{22}=\frac{1}{C_2}\qquad[22]\]
\(C_1\) et \(C_2\) étant les capacités respectives des deux conducteurs isolés dans l’espace.
On a en effet en première approximation : \[V_1=\frac{Q_1}{C_1}+\frac{Q_2}{4\pi~\varepsilon_0~r}\quad;\quad V_2=\frac{Q_2}{C_2}+\frac{Q_1}{4\pi~\varepsilon_0~r}\qquad[23]\]
On peut ensuite calculer approximativement les coefficients \(C_{ij}\) à partir des formules approchées précédentes.
Nous avons vu au chapitre précédent que l’on pouvait écrire : \[Q_i=\sum_{j=1}^{j=k}C_{ij}V_j\quad;\quad C_{ij}=\frac{P_{ij}}{\Delta}\qquad[24]\]
-
\(\Delta\) : déterminant des \((p_{ij})\)
-
\(P_{ij}\) : mineur de \(p_{ij}\) dans \(\Delta\)
On a ici (déterminant \(\Delta\)) : \[\begin{aligned} p_{11}&=\frac{1}{C_2} &&p_{12}=-\frac{1}{4\pi~\varepsilon_0~r}\\ p_{21}&=-\frac{1}{4\pi~\varepsilon_0~r}\quad &&p_{22}=\frac{1}{C_1} \end{aligned} \qquad[25]\]
On a donc : \[C_{11}\approx C_1\quad;\quad C_{22}\approx C_2\quad;\quad C_{12}=C_{21}\approx -\frac{C_1~C_2}{4\pi~\varepsilon_0~r}\qquad[26]\]
En particulier, si les deux conducteurs ont des charges égales et opposées, on peut écrire : \[(V_1-V_2)=(p_{11}+p_{22}-2~p_{12})~Q_1=\Big\{\frac{1}{C_1}+\frac{1}{C_2}-\frac{2}{4\pi~\varepsilon_0~r}\Big\}~Q_1\qquad[27]\]

