1. Définitions
Plaçons-nous dans un milieu où l’on ne rencontre que des électrons et des ions. Ce peut être le cas d’un métal, d’un semi-conducteur ou d’une étoile (la température est alors tellement élevée que l’énergie \(k~T\) est très supérieure à l’énergie de liaison.
Les équations complètes ne sont pas simples, mais un certain nombre de résultats d’une grande importance peuvent se retrouver aisément.
2. Effet d’écran (ou distance écran de Debye)
Supposons qu’un supplément local d’électrons \(\delta n_e\) produits par une cause quelconque crée la densité de charge macroscopique \(-e~\delta n_e\).
Nous allons voir que l’équilibre thermique atténue la perturbation sur une distance dont on peut évaluer l’ordre de grandeur. Il en résulte un potentiel local vérifiant : \[\Delta V=-e~\delta n_e\]
Pour une répartition sphérique (\(\delta n_e\) fonction de \(r\)) : \[V=V_0-\frac{e~\delta n_e}{3~\varepsilon_0}~r^2\qquad\text{(ordre de grandeur)}\]
Un électron situé à une distance \(r\) possède donc un supplément d’énergie potentielle : \[W=W_0+\frac{e^2~\delta n_e}{3~\varepsilon_0}~r^2\]
La population des couches \(\delta r\) est donnée par la statistique de Maxwell-Boltzmann : elle est proportionnelle à \(\exp(-W/k~T)\).
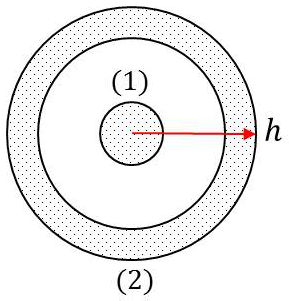
Plaçons-nous à la distance \(h\) où la population redevient normale : \[\frac{n_e+\delta n_e}{n_e}=\frac{\exp\Big(-\cfrac{W}{k~T}\Big)}{\exp\Big(-\cfrac{W_0+\delta W_h}{k~T}\Big)}\]
Soit : \[\frac{\delta n_e}{n_e}\cong\frac{\delta W_h}{k~T}\approx\frac{e^2~\delta n_e}{k~T}~h^2\]
La perturbation apparaît donc à une distance de l’ordre de : \[h=\sqrt{\frac{\varepsilon_0~k~T}{e^2~n_e}}=6,90~\sqrt{\frac{T}{n_e}}\]
Nous retrouverons cette constante d’écran dans les électrolytes.
Prenons quelques exemples pour fixer les idées sur les ordres de grandeur pour un métal, un électrolyte et un semi conducteur, pour une même température de 300 K, c’est-à-dire une température quasiment ambiante.
\[\begin{aligned} &\text{Métal~:} &&n_e=3\times 10^{22} &&h=0,07\times 10^{-9}~\rm m \\ &\text{Électrolyte~:} &&n_e=3\times 10^{18} &&h=7\times 10^{-9}~\rm m \\ &\text{Semi-conducteur~:} &&n_e=3\times 10^{14} &&h=0,07\times 10^{-6}~\rm m\end{aligned}\]
À l’échelle macroscopique, ces milieux paraissent donc neutres.
Si \(h\) est petit devant les autres dimensions qui interviennent, le milieu est appelé plasma.
3. Effet de striction ou de pincement (pinch effect)
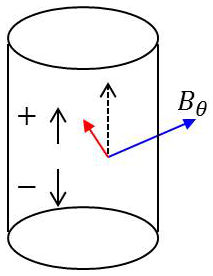Considérons un plasma siège d’un courant cylindrique de densité uniforme \(\overrightarrow{C}\).
À la distance \(r\), l’induction est : \[B_{\theta}=\mu_0~\frac{i}{2\pi~r}=\mu_0~\frac{r^2~C}{2\pi~r}=\frac{1}{2}~\mu_0~C~r\]
Les particules de vitesse \(v_{\pm}\) sont soumises toutes deux à la force suivant l’axe : \[f_{\pm}=q_{\pm}~v_{\pm}~B\]
La veine a donc tendance à se resserrer en comprimant le gaz de manière plus ou moins adiabatique. On obtient ainsi des températures de l’ordre de 106 K (\(kT\) vaut alors 100 eV).
On cherche actuellement à accroître cette température de manière à ce qu’un nombre suffisant d’ions atteignent des énergies proches du MeV afin de déclencher des réactions nucléaires.
Nota : Il importe que le plasma soit neutre, sinon la répulsion coulombienne l’emporte.
4. Fréquence de plasma
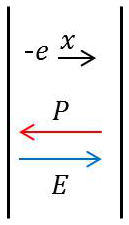Imaginons une lamelle de plasma. Nous considérerons que l’ensemble des ions est sans vitesse d’ensemble, vu leur masse. Écartons normalement l’ensemble des électrons de \(x\). Le milieu possède alors une polarisation : \[P=-n~e~x\]
Il apparaît donc un champ dépolarisant : \[E=-\frac{P}{\varepsilon_0}\]
L’ensemble des électrons est donc soumis à la force de rappel par unité de volume : \[f=-n~e~E=-\frac{n^2~e^2}{\varepsilon_0}~x\]
Écrivons l’équation du mouvement : \[m~n~\frac{dx^2}{dt^2}=-\frac{n^2~e^2}{\varepsilon_0}~x\]
Le système possède donc une pulsation de résonance : \[\omega_p=\sqrt{\frac{n~e^2}{m~\varepsilon_0}}\]
Quelques ordres de grandeur :
– pour un métal : \[n=10^{22}\qquad;\qquad \nu_p=10^{15}~\rm Hz\]
– pour un semi-conducteur : \[n=10^{14}\qquad;\qquad \nu_p=10^{11}~\rm Hz\]
