1. Module d’élasticité ou module de Young

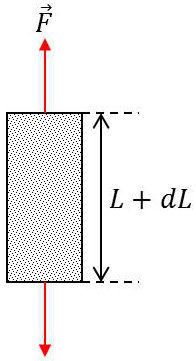Soit une barre cylindrique de section droite \(S\) et de longueur \(L\) que nous supposons formée d’un matériau isotrope. Soumettons-la à ses extrémités à un effort de traction \(F\) : il en résulte un allongement \(dL\) pour la barre.

Si \(F\) n’est pas trop important (inférieur à la limite élastique), l’allongement de la barre est proportionnel à l’effort par unité de section : \[\frac{dL}{L}=\frac{1}{E}~\frac{F}{S}\]

Le coefficient \(E\) ne dépend que du matériau qui constitue la barre (et des divers traitements, thermiques et mécaniques, qu’a subis le matériau).

C’est le module d’élasticité ou module de Young. Pour l’acier, \(E\approx 2\times 10^{11}~N/m^2\).

2. Coefficient de Poisson

En même temps qu’elle s’allonge, la barre s’amincit, la variation relative des diverses dimensions latérales (diamètre par exemple pour un cylindre de révolution) étant proportionnelle à l’allongement relatif.

Soit \(a\) une dimension latérale ; on pourra écrire : \[\frac{da}{a}=-\sigma~\frac{dL}{L}\]

Le coefficient \(\sigma\) est désigné sous le nom de coefficient de Poisson. On remarque alors que les variations relatives de longueur, de section et de volume de la barre s’expriment de la façon suivante :

\[\begin{aligned} &\frac{dL}{L}=\frac{F}{E~S}\\ &\frac{dS}{S}=-2~\sigma\frac{F}{E~S}\\ &\frac{dV}{V}=(1-2~\sigma)~\frac{F}{E~S}\end{aligned}\]

Pour une traction positive, la variation de volume est toujours positive, donc \(\sigma<1/2\). Les valeurs du coefficient de Poisson se situent généralement dans l’intervalle \([0,2,~0,4]\)

3. Parallélépipède rectangle soumis à des efforts normaux

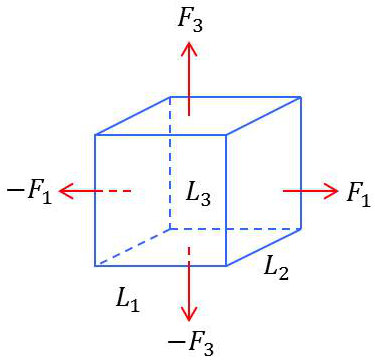Désignons par \(N_1,~N_2,~N_3\) les efforts normaux par unité de surface sur les faces du parallélépipède d’arêtes \(L_1,~L_2,~L_3\) suivant les trois axes de coordonnées.

On a donc : \[F_1=N_1~L_2~L_3\quad;\quad F_2=N_2~L_1~L_3\quad;\quad F_3=N_3~L_1~L_2\]

Les variations relatives de longueur des arêtes résultent de la superposition de ces trois efforts de traction, et l’on a, au second ordre près :

\[\begin{aligned} &a_1=\frac{dL_1}{L_1}=\frac{N_1}{E-\sigma~\cfrac{N_2+N_3}{E}} &&\text{allongement relatif}~/~Ox_1\\ &a_2=\frac{dL_2}{L_2}=\frac{N_2}{E-\sigma~\cfrac{N_1+N_3}{E}} &&\text{allongement relatif}~/~Ox_2\\ &a_3=\frac{dL_3}{L_3}=\frac{N_3}{E-\sigma~\cfrac{N_1+N_2}{E}} &&\text{allongement relatif}~/~Ox_3\end{aligned}\]

On a coutume de désigner par \(\theta\) la dilatation \([a_1 + a_2 + a_3]\). On peut écrire dès lors : \[\theta=\frac{1-2~\sigma}{E}~(N_1+N_2+N_3)\]

Remarquons en passant que, pour une surpression uniforme : \[N_1=N_2=N_3=-\delta P\]

On en tire le coefficient de compressibilité : \[\chi=-\frac{1}{V}~\frac{\delta V}{\delta P}=-\frac{\theta}{\delta P}=3~\frac{(1-2\sigma)}{E}\]

4. Coefficients de Lamé

Les équations que nous avons écrites lient les déformations aux tensions dans un parallélépipède rectangle soumis uniquement à des efforts normaux. Résolvons-les par rapport aux travaux normaux. Nous obtenons : \[a_1=\frac{1+\sigma}{E}~N_1-\frac{\sigma}{E}~(N_1+N_2+N_3)=\frac{1+\sigma}{E}~N_1-\frac{\sigma}{1-2\sigma}~\theta\]

D’où il vient : \[N_1=\frac{E\sigma}{(1+\sigma)~(1-2\sigma)}~\theta+\frac{E}{1+\sigma}~a_1\]

Ainsi apparaissent deux coefficients \(\lambda\) et \(\mu\) appelés coefficients de Lamé, de sorte que l’on peut écrire généralement : \[N_i=\lambda~\theta+2~\mu~a_i\]

Ces coefficients suffisent à définir complètement toutes les propriétés élastiques du matériau. Rappelons que nous nous sommes restreints aux matériaux isotropes. En particulier, on peut calculer, à partir de \(\lambda\) et \(\mu\), les trois autres coefficients :

\[\begin{aligned} \sigma&=\frac{\lambda}{2~(\lambda+\mu)}\\ E&=\mu~\frac{3~\lambda+2~\mu}{\lambda+\mu}\\ \chi&=\frac{3}{3~\lambda+2~\mu}\end{aligned}\]

5. Module de rigidité

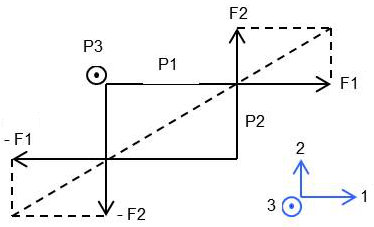Nous allons maintenant appliquer aux faces du parallélépipède des forces tangentielles et non plus normales.

Sur la figure ci-contre, le parallélépipède est représenté avec son arête \(P_3\) perpendiculaire au plan de la figure.

Appliquons à la face supérieure (vue de bout) une force tangentielle, uniformément répartie sur la surface \(P_2P_3\). L’équilibre du parallélépipède exige :

1. que nous appliquions une force opposée \((- F_1\)) à la face intérieure ;

2. que nous appliquions également aux faces latérales des efforts tangentiels annulant le couple des deux premières forces. On voit immédiatement que l’égalité des couples exige que les efforts tangentiels par unité de surface soient les mêmes sur les 4 faces et qu’ils soient dirigées comme l’indique la figure.

Remarque

On pourrait évidemment équilibrer le parallélépipède par des efforts normaux, sur la face intérieure par exemple ; mais ces efforts normaux seraient obligatoirement distribués de façon non uniforme sur cette surface, ce qui doit être exclu s’il s’agit d’un parallélépipède infiniment petit.

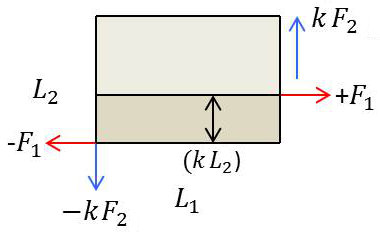La portion du parallélépipède située au-dessous d’un plan parallèle à la face \([L_1,~L_2]\) et de cote \([k~L_2~;~k < 1]\) est soumise aux efforts extérieurs \((k~F_2)\) et \((-k~F_2)\) dans le sens vertical (uniformité de la répartition des forces sur les surfaces), puis \((- F_1)\) dans le sens horizontal.

L’équilibre de cette portion exige que le reste du parallélépipède exerce sur elle le long de la surface de contact un effort tangentiel (ou effort tranchant) \((+ F_1)\).

On pourrait faire le même raisonnement pour l’autre direction (sections perpendiculaires à \(L_1\)) et en déduire ainsi que chaque section parallèle aux plans \([L_2,~L_3]\) ou \([L_1,~L_3]\) est soumis aux mêmes efforts tranchants, quelle que soit sa position.

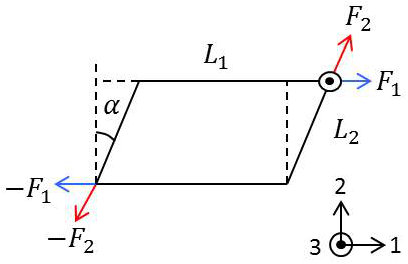La déformation qui en résulte pour le parallélépipède est donc un glissement des couches atomiques les unes sur les autres qui transforme en un parallélogramme la section \([L_1,~L_2]\).

L’effort \(F_1\) nécessaire pour une déformation angulaire \(\alpha\) est donc indépendante de \(L_2\) et proportionnelle à \(L_3\), ce qui est évident.

On démontrerait de même que l’effort \(F_2\) qu’il faut associer nécessairement à \(F_1\) pour l’équilibre du parallélépipède, est, pour une déformation angulaire donnée \(\alpha\), indépendant de \(L_1\) et proportionnel à \(L_3\).

L’égalité des couples au signe près exige que \(F_2~L_1=F_1~L_2\). Il en résulte \(F_1\) est proportionnel à \(L_1\) et \(F_2\) proportionnel à \(_L2\).

On a en effet : \[\frac{F_1}{L_1}=\frac{F_2}{L_2}\]

les deux termes étant proportionnels à \(L_3\) et indépendants, le premier de \(L_2\) et le second de \(L_1\).

La valeur commune des quotients \(F_1/L_1~L_3\) et \(F_2/L_2~L_3\) est donc indépendante des dimensions du parallélépipède et ne dépend que de sa formation angulaire \(\alpha\) .

Si nous désignons par \(T_3\) cette valeur commune qui représente l’effort tangentiel par unité de surface appliqué perpendiculairement à la direction \(L3\) aux faces adjacentes aux arêtes \(L_3\), nous obtenons \[T_3=G~\alpha\]

Il y a proportionnalité des efforts aux déformations, tant que celles-ci restent petites.

Le coefficient \(G\) est désigné sous le nom de module de rigidité du matériau (supposé isotrope) constituant le parallélépipède. On montre que \(G\) s’identifie avec \(\mu\), second coefficient de Lamé, cette dernière notation étant retenue de préférence à \(G\).

Sa valeur étant égale à \(E/2~(1+\sigma)\) et les valeurs de \(\sigma\) s’échelonnant généralement entre 0,2 et 0,4, le module de rigidité \(\mu\) est de l’ordre de \(0,4~E\).