1. Tenseur des efforts

Découpons un solide le long d’un plan \(P\) normal au vecteur \(\overrightarrow{N}\) et enlevons la partie située du côté du plan \(P\) indiquée par le vecteur \(\overrightarrow{N}\), c’est-à-dire du côté de la normale positive au plan de coupe.

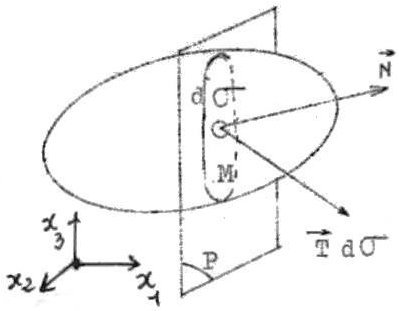Le reste du solide demeurera dans un état invariable si nous avons soin d’appliquer en tous points du plan de coupe des efforts convenables, ceux-là même qui étaient exercés par la portion du solide que nous avons supprimée.

Ces efforts étaient répartis de façon continue : il nous faut donc appliquer à l’élément \(d\sigma\) de la surface de coupe entourant un point \(M\) un effort \(\overrightarrow{T} d\sigma\).

Le vecteur \(\overrightarrow{T}\) représente l’effort exercé par unité de surface, le long de l’élément de surface \(d\sigma\), par la portion du solide située du côté de la normale positive sur celle qui se trouve du côté de la normale négative.

Remarque

Le vecteur \(\overrightarrow{T}d\sigma\) représente la force exercée sur l’élément \(d\sigma\) par la portion de solide située du côté de la normale positive. Ce ne sont que de telles forces que nous considèrerons dans ce qui va suivre. Ce faisant, nous supposerons implicitement que l’ensemble des efforts exercés sur la portion de surface \(d\sigma\) par le solide situé du côté de la normale positive se réduit effectivement à une force, à condition que l’élément \(d\sigma\) soit assez petit.

Il s’agit là d’une hypothèse qui n’est pas obligatoirement vérifiée, comme on l’a montré récemment. Il peut arriver, en effet, que les atomes eux-mêmes soient soumis de la part des atomes environnants à des couples et non pas seulement à des forces. Sans insister sur ce point, signalons cependant que la présence d’une telle distribution volumique de couples autorise la dissymétrie du tenseur des efforts, même en l’absence de forces extérieures appliquant à l’élément de volume un couple de l’ordre de grandeur de \(dv\).

Le nombre de coefficients indépendants permettant d’exprimer les relations entre les tensions et les déformations s’élève à 45 (au lieu de 21) pour un cristal triclinique ; nous supposerons dans ce qui suit que de tels couples inter-atomiques n’existent pas.

Découpons alors dans le solide un petit parallélépipède d’arêtes parallèles aux axes de coordonnées \(dx_1,~dx_2,~dx_3\). Désignons par les aires respectives des faces perpendiculaires aux axes de coordonnées, soit \(d\sigma_1=dx_2~dx_3\), etc.

1.1. Résultante des efforts de tension sur un élément de volume

Les directions positives des normales aux faces sont celles des axes de coordonnées. Nous allons calculer la résultante générale des efforts exercés sur le petit parallélépipède par le reste du solide, en remarquant que si, sur une face, le reste du solide se trouve du côté de la normale positive, il se trouve, sur la face opposée, du côté de la normale négative.

Si nous désignons par \(\overrightarrow{T_1},~\overrightarrow{T_2},~\overrightarrow{T_3}\) les efforts par unité de surface qui s’exercent sur les trois faces issues d’un même sommet, la résultante générale des efforts sur les six faces a pour valeur : \[\Big(\frac{\partial\overrightarrow{T_1}}{\partial x_1}\Big)~dx_1~d\sigma_1+\Big(\frac{\partial\overrightarrow{T_2}}{\partial x_2}\Big)~dx_2~d\sigma_2+\Big(\frac{\partial\overrightarrow{T_3}}{\partial x_3}\Big)~dx_3~d\sigma_3\]

soit, en désignant par \(dv\) le volume du parallélépipède : \[\Big(\frac{\partial\overrightarrow{T_1}}{\partial x_1}+\frac{\partial\overrightarrow{T_2}}{\partial x_2}+\frac{\partial\overrightarrow{T_3}}{\partial x_3}\Big)~dv\]

Désignons par \(t_{ij}\) la composante suivant \(Ox_j\) du vecteur \(\overrightarrow{T_i}\). La composante suivant \(Ox_1\) de l’ensemble des efforts de tension sur les six faces est donnée par : \[\Big(\frac{\partial t_{11}}{\partial x_1}+\frac{\partial t_{21}}{\partial x_2}+\frac{\partial t_{31}}{\partial x_3}\Big)~dv\]

L’équilibre exige que soit appliquée de l’extérieur une force proportionnelle à l’élément de volume (gravitation par exemple) ou que le petit parallélépipède ait une accélération \(\overrightarrow{\gamma}\) et, par suite, soit soumis à une force d’inertie (\(-\rho~dv~\overrightarrow{\gamma}\)), \(\rho\) étant la masse spécifique.

D’une manière générale, désignons par (\(X_1~dv,~X_2~dv,~X_3~dv\)) les composantes de la force qui se trouve appliquée à l’élément de volume, soit par un champ de forces extérieur, soit par suite de l’inertie, nous pourrons écrire les équations d’équilibre : \[\sum_i\frac{\partial t_{ij}}{\partial x_i}~X_j=0\qquad\text{3 équations}\]

1.2. Symétrie du tenseur des efforts

Nous allons maintenant étudier les quantités \(t_{ij}\) dans un très petit volume du solide où l’on peut les considérer comme constantes. Ces quantités satisfont aux relations de symétrie \(t_{ij}=t_{ji}\).

En effet, supposons qu’il n’existe pas de forces extérieures capables d’appliquer à l’élément \(dv\) du solide un couple du même ordre de grandeur que \(dv\), c’est-à-dire du 3° ordre en \(dx\). Nous excluons ainsi le cas d’une substance aimantée placée dans un champ magnétique par exemple, mais nous n’excluons pas les forces d’inertie de rotation qui conduisent à des couples du 5° ordre. Nous devons alors écrire que le couple total des forces de tension sur les faces exercent sur le petit parallélépipède est nul au 4° ordre.

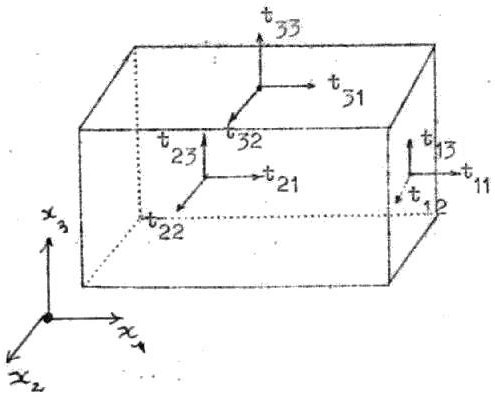Calculons la composante de ce couple suivant \(Ox_3\). Ne contribuent pas à cette composante :

– les forces normales \(t_{ii}~d\sigma_i\) sur les 6 faces (bras de levier nul) ;

– les forces tangentielles \(t_{31}~d\sigma_3\) et \(t_{32}~d\sigma_3\) (bras de levier // \(Ox_3\) ) ;

– les forces parallèles à \(Ox_3\) du type \(t_{i3}~d\sigma_i\).

On n’a représenté les efforts par unité de surface que sur 3 des 6 faces. Les efforts sur les faces opposées sont opposés au 3° ordre près.

Il ne subsiste donc que les forces suivantes :

\[\begin{aligned} &t_{12}~d\sigma_1~~\text{et}~-t_{12}~d\sigma_1~~~\text{formant le couple}~-t_{12}~d\sigma_1~dx_1~;\\ &t_{21}~d\sigma_2~~\text{et}~-t_{21}~d\sigma_2~~~\text{formant le couple}~+t_{21}~d\sigma_2~dx_2.\end{aligned}\]

Comme \(d\sigma_1~dx_1=d\sigma_2~dx_2=dv\), il reste un couple du 3° ordre en \(dx\) : \[(t_{21}-t_{12})~dv=0\qquad\text{soit :}\quad t_{12}=t_{21}\]

D’une manière générale \(t_{ij}=t_{ji}\).

1.3. Effort sur un élément \(d\sigma\) d’orientation quelconque

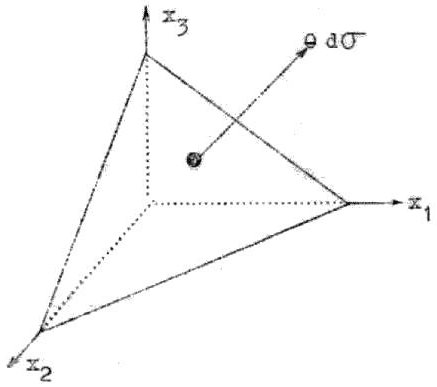Nous prenons pour élément \(d\sigma\) la base d’une pyramide dont les faces sont parallèles aux plans de coordonnées.

Soient \(n_1,~n_2,~n_3\) les cosinus directeurs de la normale à la base \(d\sigma\). Les faces latérales de la pyramide ont pour aires respectives : \(n_1~d\sigma,~n_2~d\sigma,~n_3~d\sigma\).

Soient \(\theta_1~d\sigma,~\theta_2~d\sigma,~\theta_2~d\sigma\) les composantes de l’effort de traction qui s’exerce sur la base. L’équilibre du tétraèdre exige les égalités : \[\theta_1~d\sigma-t_{11}~n_1~d\sigma-t_{21}~n_2~d\sigma-t_{31}~n_3~d\sigma=0\]

(force totale nulle suivant \(Ox_1\)).

Il y a des égalités analogues suivant les deux autres axes et on a en définitive :

\[\begin{aligned} \theta_1=n_1~t_{11}+n_2~t_{21}+n_3~t_{31}\\ \theta_2=n_1~t_{12}+n_2~t_{22}+n_3~t_{32}\\ \theta_3=n_1~t_{13}+n_2~t_{23}+n_3~t_{33}\end{aligned}\]

Ces formules permettent de calculer les efforts sur une surface d’orientation quelconque. Elles nous permettent, en outre, de calculer comment se transforment les \(t_{ij}\) dans un changement d’axes de coordonnées. Nous nous bornerons à une rotation du trièdre de référence qui reste donc trirectangle et orienté à droite. Nous passons des trois vecteurs de base \(\overrightarrow{e_1},~\overrightarrow{e_2},~\overrightarrow{e_3}\) (2 à 2 orthogonaux), le trièdre ayant même sens \(\overrightarrow{E_1},~\overrightarrow{E_2},~\overrightarrow{E_3}\) et les nouveaux vecteurs de base étant définis par les relations :

\[\begin{aligned} \overrightarrow{E_{\lambda}}=\sum_i \alpha_{\lambda}^i~\overrightarrow{e_i}\quad&;\quad \alpha_{\lambda}^i=\cos(\overrightarrow{e_i},~\overrightarrow{E_i})\\ \overrightarrow{e_i}=\sum_{\lambda} \alpha_i^{\lambda}~\overrightarrow{E_{\lambda}}\quad&;\quad \alpha_i^{\lambda}=\alpha_{\lambda}^i\end{aligned}\]

Nous nous proposons de calculer \(\theta_{\lambda\mu}\), composante suivant \(\overrightarrow{E_{\mu}}\) de l’effort qui s’exerce par unité de surface sur un élément de surface perpendiculaire à \(\overrightarrow{E_{\lambda}}\).

Soit \(\overrightarrow{\theta_{\lambda}}\) cet effort. Les composantes suivant les anciens vecteurs de base \(\overrightarrow{e_i}\) sont : \[\theta_{\lambda}^i=\sum_j\alpha_{\lambda}^j~t_{ji}\qquad\text{(formules obtenues précédemment)}\]

On a donc : \[\overrightarrow{\theta_{\lambda}}=\sum_{ji}\alpha_{\lambda}^j~t_{ji}~\overrightarrow{e_i}\]

Soit, en fonction de \(\overrightarrow{E_{\mu}}\) : \[\overrightarrow{\theta_{\lambda}}=\sum_{ji\mu} \alpha_{\lambda}^j~t_{ji}~\alpha_i^{\mu}~\overrightarrow{E_{\mu}}\]

On a donc en définitive : \[\theta_{\lambda\mu}=\sum_{ij} \alpha_{\lambda}^j~\alpha_{\mu}^i~t_j\]

C’est la formule de transformation d’un tenseur du second ordre. En fait, c’est en élasticité que de telles formules de transformation sont apparues pour la première fois. D’où le nom de tenseurs, donné à ces ensembles de composantes à 1, 2 ou n indices.

Nous ne nous occupons pas ici de covariance ou de contravariance, du fait que nous nous restreignons à des systèmes de référence trirectangulaires où la distinction entre composantes covariantes et composantes contravariantes disparaît.

La restriction à des trièdres de même sens (à droite) nous a permis, en outre, de représenter l’élément de surface avec un seul indice, alors qu’il constitue, en fait, une composante d’un tenseur antisymétrique du second ordre. Le tenseur des efforts est, en toute rigueur, un tenseur du troisième ordre que nous ramenons à une densité tensorielle \(t_{ij}\) en choisissant un ordre de numérotage pour les trois axes. Nous n’envisagerons que des rotations du système d’axes et pourrons considérer simplement que les \(t_{ij}\) sont les composantes d’un tenseur symétrique du second ordre.

Si nous choisissons comme axes de coordonnées les trois axes principaux trirectangulaires de ce tenseur (voit plus loin), nous annulerons les termes à indices différents. Tout système d’efforts peut donc être considéré comme résultant de la superposition de trois efforts normaux suivant trois directions orthogonales. Pour un système de référence trirectangle quelconque, on représente souvent les \(t_{ij}\) sous la forme : \[\begin{pmatrix} t_{11}&t_{12}&t_{13}\\ t_{21}&t_{22}&t_{23}\\ t_{31}&t_{32}&t_{33} \end{pmatrix} \quad = \quad \begin{pmatrix} N_1&T_3&T_2\\ T_3&N_2&T_1\\ T_2&T_1&N_3 \end{pmatrix}\]

Les composantes \(N_i\) représentent les efforts normaux, les composantes \(T_i\) représentent les efforts tangentiels ou efforts tranchants.

2. Tenseur des déformations locales

Nous nous proposons d’étudier la déformation la plus générale d’un solide élastique. Donnons à chacun des points du solide un déplacement, fonction de sa position \(\overrightarrow{u}=f(x_1,~x_2,~x_3)\).

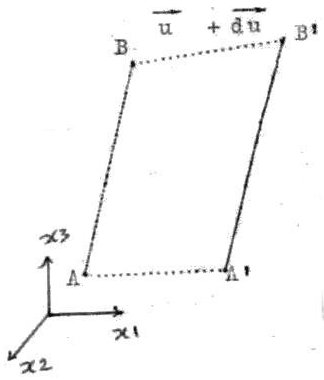Soit deux points voisins du solide \(A(x_1,~x_2,~x_3)\) et \(B(x_1+dx_1,~x_2+dx_2,~x_3+dx_3)\). Ils se déplacent de \(\overrightarrow{u}\) et de \(\overrightarrow{u}+\overrightarrow{du}\). Le vecteur \(\overrightarrow{AB}\) est donc modifié de \(d(\overrightarrow{AB})=d\overrightarrow{u}\) dont les composantes sont : \[du_j=\sum_i\frac{\partial u_j}{\partial x_i}~dx_i\]

Cherchons à mettre en évidence la déformation locale du solide en calculant la modification de longueur du segment \(AB\) ou, ce qui revient au même, la modification de \(\overline{AB^2}=ds^2\).

En supposant que \(\overline{du}\ll \overline{AB}\), nous obtenons: \[d(ds^2)=d(\overline{AB^2})=2~\overline{AB}~d(\overline{AB})=2\sum_{ji}\frac{\partial u_j}{\partial x_i}~dx_i~dx_j\]

Ce qui peut encore s’écrire sous la forme : \[d(ds^2)=2\sum_i\frac{\partial u_i}{\partial x_i}~(dx_i)^2=\sum_{i\neq j} \Big(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\Big)~dx_i~dx_j\]

Ou bien encore : \[d(ds^2)=2\sum_{ij}d_{ij}~dx_i~dx_j\qquad\text{avec :}\quad d_{ij}=\frac{1}{2}~\Big(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\Big)\]

Les \(d_{ij}\) forment les composantes d’un tenseur du second ordre, manifestement symétrique. Ce tenseur suffit à représenter l’ensemble des déformations du solide au voisinage du point \(A\), puisqu’il suffit à déterminer la modification de longueur de tous les petits segments tracés dans le solide au voisinage de \(A\), que ces segments aient ou non une extrémité en \(A\).

Nous désignerons le tenseur \(d_{ij}\) sous le nom de tenseur des déformations. Pour représenter l’ensemble des déformations d’un solide macroscopique, il faut évidemment attacher à chaque point du solide un tenseur qui représente les déformations locales au voisinage de ce point, c’est-à-dire considérer le champ de tenseurs \(d_{ij}\) dans toute l’étendue du solide déformé.

Il est aisé de reconnaître à quelles déformations simples correspondent les diverses composantes du tenseur \(d_{ij}\). En effet, une composante du type \(d_{ii}=\partial u_i / \partial x_i \) correspond manifestement à une dilatation locale suivant la direction \(Ox_i\).

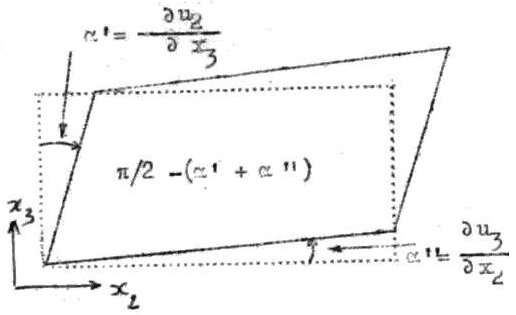Par ailleurs, les deux composantes égales \(d_{23}\) et \(d_{32}\) (par exemple) correspondent toutes deux à la même déformation.

À savoir, (cf. figure ci-contre), un glissement qui transforme la face \(dx_2~dx_3\) d’un petit parallélépipède rectangle (initialement) ayant un de ses sommets en \(A\) et dont les arêtes sont initialement parallèles aux axes de coordonnées, en un parallélogramme dont l’angle en \(A\) sur la face \(dx_2~dx_3\) est devenu : \[\frac{\pi}{2}-\Big(\frac{\partial u_2}{\partial x_3}+\frac{\partial u_3}{\partial x_2}\Big)=\frac{\pi}{2}-\alpha\qquad\text{avec :}\quad \alpha=2~d_{23}\]

De même que pour le tenseur des efforts, la symétrie réduit à 6 le nombre de composantes indépendantes du tenseur des déformations, nous représenterons l’ensemble de ces composantes dans la notation :

\[\begin{pmatrix} d_{11}&d_{12}&d_{13}\\ d_{21}&d_{22}&d_{23}\\ d_{31}&d_{32}&d_{33} \end{pmatrix} \quad = \quad \begin{pmatrix} a_1&g_3&d_2\\ g_3&a_2&g_1\\ g_2&g_1&a_3 \end{pmatrix}\]

Les \(a_i\) correspondent aux dilatations locales suivant les axes de coordonnées. Un \(g_k=d_{ji}\) correspond à une déformation locale (glissement) dans laquelle l’angle (initialement droit) des directions positives des arêtes \(dx_i\) et \(dx_j\) d’un petit parallélépipède diminue d’un angle \(\alpha=2~g_k\).

3. Propriétés des tenseurs "efforts et déformations"

Les composantes \(t_{ij}\) du tenseur des efforts se modifient bien entendu lors d’une rotation du système d’axes trirectangles, comme nous l’avons vu plus haut ; il en est de même des composantes \(d_{ij}\) du tenseur des déformations. Il en résulte toutefois des propriétés générales des tenseurs que la somme des termes diagonaux est dans les deux tenseurs invariante, lors de toute rotation du système d’axes trirectangle : \[\sum_{i=1}^3t_{ii}=\text{cte}\qquad\text{et}\qquad\sum_{i=1}^3d_{ii}=\text{cte}=\theta\quad\text{(dilatation)}\]

Le nombre de composantes indépendantes de chaque tenseur est égal à 3 ; il est possible, par un choix convenable du système d’axes trirectangle, d’annuler les 6 composantes \(t_{ij}\) à indices différents qui sont deux à deux égales.

Le tenseur \(t_{ij}\) est dit, dans ces conditions, rapporté à ses axes principaux ; seules sont alors différentes de zéro ses composantes diagonales du type \(t_{ii}\). Il en résulte que le système d’efforts locaux le plus général, représenté dans le système d’axes initial par trois composantes \(N_i\) et trois composantes \(T_i\), peut, dans un système d’axes trirectangle convenablement choisi, être réduit à trois composantes \(N'_i\).

En d’autres termes, tout système d’efforts peut être représenté par trois efforts normaux dirigés suivant les axes principaux du tenseur des efforts. De la même façon, toute déformation locale peut être représentée par l’ensemble de trois dilatations suivant les trois axes principaux du tenseur des déformations.

Il faut néanmoins remarquer que, dans le cas général d’un solide cristallin (monocristal) soumis à des efforts quelconques, les axes principaux des deux tenseurs ne coïncident pas et qu’il est donc impossible de réduire simultanément ces deux tenseurs à leurs axes principaux par un choix convenable des axes de coordonnées.

Dans le cas d’un cristal, on pourra, par exemple, considérer que tout système d’efforts se réduit à un ensemble d’efforts normaux (au voisinage d’un point), mais que les déformations correspondantes au voisinage de ce point, mesurées dans le même système d’axes, pourront comporter des glissements. Nous allons voir que ce n’est que dans le cas d’un matériau isotrope que les deux tenseurs admettent les mêmes axes principaux.

Remarquons en outre que le tenseur des efforts et le tenseur des déformations ont été définis au voisinage d’un point du solide ; l’ensemble des efforts et des déformations au sein de tout solide doit être représenté par deux champs de tenseurs. Même dans le cas d’un solide isotrope, un système d’efforts général ne peut être ramené à ses axes principaux qu’au voisinage d’un point, la direction des axes principaux communs aux deux tenseurs variant d’un point à l’autre du solide isotrope.

Il serait faux de prétendre par exemple que l’ensemble des efforts au sein d’un solide de dimensions importantes peut être considéré comme un ensemble d’efforts normaux, ce qui est bien évident.