1. Position du problème

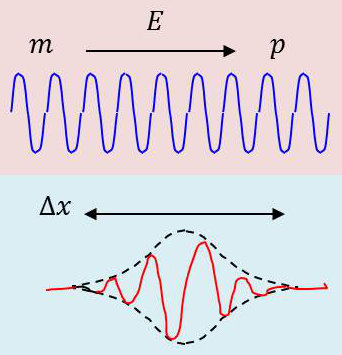Les ondes sinusoïdales d’amplitude constante et d’étendue infinie ne se présentent en fait que comme un cas particulier des ondes progressives. On peut être tenté d’associer à un corpuscule isolé une onde d’étendue limitée qui se déplacera en même temps que le corpuscule.

Ainsi, l’observateur qui pourrait s’apercevoir de la présence de l’onde déterminera à peu près la position du corpuscule, car l’onde a en fait une certaine étendue.

On pourra donc connaître la position du corpuscule mais avec une incertitude \(\Delta x\) correspondant à la largeur de l’onde, ce qui peut se comprendre.

Les grandeurs cinétiques non quantifiées de la particule sont sa vitesse, sa quantité de mouvement et son énergie totale.

Désignons par \(q\) l’affixe de la particule. On a donc :

\[\begin{aligned} \overrightarrow{v}&=\frac{d}{dt}\overrightarrow{q}\quad;\quad\overrightarrow{p}=m~\overrightarrow{v}\\ W&=m~c^2=\frac{m_0~c^2}{\sqrt{1-v^2/c^2}}\cong m_0~c^2+\frac{1}{2}~m~v^2\end{aligned}\]

1.1. Onde associée

Les phénomènes de diffraction imposent que l’on associe à ce mouvement une onde plane de fréquence : \[\nu =\frac{E}{h}\]

et de vecteur d’onde : \[\overrightarrow{k}=\cfrac{\overrightarrow{p}}{h}\]

Dans le cas d’une onde plane, ce vecteur est normal aux plans d’onde, dirigé dans le sens de propagation de l’onde et de module \(k=1/\lambda\).

L’onde est alors représentée à l’aide d’une fonction \(\psi\) exprimée par : \[\psi=A~\exp\{j~2\pi~(v ~t-\overrightarrow{k}\cdot\overrightarrow{q})\}=A~\exp\{j~(\omega~t-\overrightarrow{k}\cdot\overrightarrow{q})\}\]

Si une telle onde seule représente une particule, il n’y a pas de raison de localiser cette particule en un point de l’espace ; cette onde représente une particule qui possède une égale probabilité de se trouver n’importe où.

1.2. Train d’ondes planes

Pour se représenter une onde localisée dans l’espace et en mouvement, il est naturel de considérer une fonction d’onde de la forme (voir figure ci-dessus) : \[\psi=\frac{1}{\sqrt{\Delta x~\sqrt{2\pi}}}~\exp\big\{-\frac{(x-x_0)^2}{4~\Delta x^2}+j~(\omega~t-k_0~x)\big\}\]

Il s’agit tout simplement d’une onde sinusoïdale modulée par une gaussienne centrée sur \(x_0\) et d’écart type \(\sqrt{x}\).

Les facteurs numériques assurent la normalité de \(\psi~\psi^*\), c’est-à-dire :

\[\begin{aligned} &\int_{_\infty}^{+\infty}\psi~\psi^*~dx=1\\ \text{avec :}\quad &\psi\psi^*=\frac{1}{\Delta x~\sqrt{2\pi}}~\exp\big\{-\frac{(x-x_0)^2}{2~\Delta x^2}\big\}\end{aligned}\]

Ce train d’ondes peut être décomposé en une somme intégrale d’ondes sinusoïdales de nombre d’ondes variables \(k\) : \[\psi=\int A(k)~\exp\{j~(\omega~t-k~x)\}~dk\]

\(A(k)\) étant la transformée de Fourier de \(\psi\).

Or, on démontre que la transformée d’une gaussienne est encore une gaussienne, le produit des écarts quadratiques moyens des deux gaussiennes étant égal à \(1/2\) : \[2~\Delta x^2~\Delta k^2=\frac{1}{2}\quad\Rightarrow\quad\Delta x~\Delta k=\frac{1}{2}\quad \Rightarrow\quad\Delta x~\Delta p_x=\frac{\hbar}{2}\]

On démontrerait qu’un train de toute autre forme conduirait à une distribution plus large en \(k\) soit :

\[\begin{aligned} \Delta x~\Delta k_x=\frac{1}{2}\quad;\quad\Delta x~\Delta p_x~\geq~\frac{\hbar}{2}\\ \Delta y~\Delta k_y=\frac{1}{2}\quad;\quad\Delta y~\Delta p_y~\geq~\frac{\hbar}{2}\\ \Delta z~\Delta k_z=\frac{1}{2}\quad;\quad\Delta z~\Delta p_z~\geq~\frac{\hbar}{2}\end{aligned}\]

Par analogie : \[\Delta t~\Delta\nu~\geq~\frac{1}{2} \quad;\quad \Delta t~\Delta E~\geq~\frac{\hbar}{2}\]

1.3. Principe d’incertitude

Nous constatons que les propriétés ondulatoires et corpusculaires ne peuvent être représentées par un formalisme mathématique unique que si l’on admet une incertitude sur la position et la vitesse d’une part et sur l’énergie de l’autre.

Les relations sont l’expression du principe d’Heisenberg :

1. Si une particule est parfaitement localisée en un point \((x,~y,~z)\), sa vitesse a une probabilité uniforme d’avoir n’importe quelle valeur.

2. Si la vitesse est parfaitement connue, la particule est située n’importe où dans l’espace.

Conséquences

1. À 0 K, les particules ne sont pas au repos.

2. Si une particule radioactive de période T émet des \(\gamma\), ceux-ci ont une largeur de raie en fréquence supérieure à \(1/2~\pi~T\).

1.4. Vitesse de phase et vitesse de groupe

Un train d’onde est la superposition d’ondes de vecteurs d’onde voisins centrés autour de \(k_0\) et de fréquences voisines centrées autour de \(\nu_0\).

La vitesse de phase moyenne est : \[\overrightarrow{v_{\phi}}=\nu_0~\frac{\overrightarrow{k_0}}{k^2}\qquad (\nu_p=\frac{\nu_0}{k_0}=\nu_0~\lambda_0)\]

Exprimons \(\psi\) comme une somme de termes en \(\exp\{j~2\pi~(\nu~t-\overrightarrow{k}\cdot\overrightarrow{q})\}\). Les coordonnées \(\{t_m,~q_m\}\) du maximum du train sont données avec cette condition que l’argument de l’exponentielle soit nul pour chaque onde composante :

– Pour l’onde (1) : \[\nu_1~t_m=\overrightarrow{k_1}\cdot\overrightarrow{q_m}\]

– Pour l’onde (2) : \[\nu_2~t_m=\overrightarrow{k_2}\cdot\overrightarrow{q_m}\]

Par soustraction : \[\delta v~t_m=\delta\overrightarrow{k}\cdot\overrightarrow{q_m}\]

La vitesse du groupe est celle du maximum, soit : \[\overrightarrow{v_g}=\frac{\overrightarrow{q_m}}{t_m}\qquad \text{de composantes~:}\quad\Big\{\frac{\partial \nu}{\partial k_1},~\frac{\partial \nu}{\partial k_2},~\frac{\partial \nu}{\partial k_3}\Big\}\]

C’est-à-dire : \[\overrightarrow{v_g}=\overrightarrow{\rm grad}(\nu)\]

1.5. Parabole de la particule libre

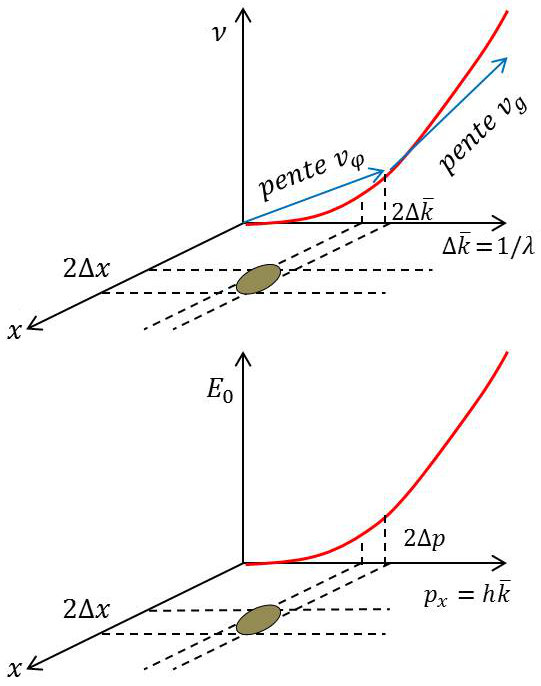Soit une particule de masse \(M\) et de vitesse \(v\).

Sa quantité de mouvement est : \[p=M~v\]

L’énergie cinétique est : \[E_c=\frac{1}{2}~M~v^2=\frac{p^2}{2~M}\qquad(\text{parabole})\]

Le nombre d’onde (moyen) est : \[\hat{k}=\frac{M~v}{h}\]

La fréquence associée est : \[\nu =\frac{M~v^2}{2~h}=\frac{h~\hat{k}^2}{2~M}\qquad(\text{parabole})\]

La vitesse de phase est : \[v_{\varphi}=\frac{v}{\hat{k}}=\frac{v}{2}\]

La vitesse de groupe est : \[v_g=\frac{\partial v }{\partial\hat{k}}=v\]

Sur la première figure ci-dessus, dans le premier espace, le point représentatif est probablement dans l’aire hachurée, voisine de l’unité. En-dessous, dans l’espace \([x,~p_x]\) le point représentant la particule est avec une probabilité notable dans une surface dont l’aire est de l’ordre de grandeur de \(h\).

Nota :

Dans le cas du photon, la courbe \(v =f(\hat{k})\) est une droite \([v =k~c]\).

La vitesse de groupe et la vitesse de phase sont égales à \(c\) dans le vide.

2. Relations d’Heinsenberg

La relation de Planck – Einstein (1) et celle de Louis de Broglie (2) réalisent la liaison entre les propriétés de type corpusculaire (énergie et quantité de mouvement d’entités discrètes) et les propriétés de type ondulatoire (périodicités spatiotemporelles).

Leur existence même implique que soient inapplicables les concepts de corpuscule ou d’onde aux particules quantiques. Plus précisément, elles permettent de cerner le domaine de validité approximative de ces concepts. C’est là l’un des rôles essentiels des relations de d’incertitude de Heisenberg.

2.1. Première relation (spatiale) de Heisenberg

Si l’on considère une particule quantique qui occupe un domaine spatial d’extension \(\Delta x\) limité, la longueur d’onde \(\lambda\) (ou la fréquence spatiale \(k=1/\lambda\) qui lui est associée) ne peut être précisée de façon absolue. En effet, un phénomène de longueur d’onde bien déterminée est rigoureusement périodique et possède donc une extension spatiale infinie.

Dans le cas présent, si la dimension \(\Delta x\) de l’objet correspond à un nombre de périodes approximatif \(n\), la longueur d’onde moyenne sera donnée par : \[\lambda=\frac{\Delta x}{n}\]

et la fréquence spatiale par : \[k=\frac{n}{\Delta x}\]

Or, le nombre de périodes ne peut pas être défini à mieux qu’une unité près, puisque le phénomène, n’étant pas rigoureusement périodique, a un début et une fin qui ne correspondent pas à des périodes que l’on puisse nettement distinguer.

Il en résulte une extension \(\Delta k\) de la fréquence spatiale \(k\), liée à l’incertitude \(\Delta n\geq 1\) sur le nombre de périodes \(n\), soit : \[\Delta k~\geq~\frac{1}{\Delta x}\qquad\text{ou encore :}\quad \Delta k~\Delta x~\geq~1\]

Jusqu’ici le raisonnement vaut pour un phénomène ondulatoire et lie son extension en configuration (spatiale) \(\Delta x\) à son extension en fréquence (spatiale) \(\Delta k\). Cependant (voir chapitre précédent), à une certaine extension en fréquence spatiale \(\Delta k\) correspond nécessairement une extension en quantité de mouvement \(\Delta p=h~\Delta k\).

D’où la relation de Heisenberg : \[\Delta p~\Delta x~\geq~h\]

Elle est ici conçue comme reliant l’extension spatiale \(\Delta x\) d’un objet quantique, sa dimension géométrique, à la largeur du spectre \(\Delta p\) des valeurs de sa quantité de mouvement.

Cette relation montre immédiatement qu’une particule quantique ne peut être assimilée à une particule classique puisqu’un tel objet ne peut être localisé ponctuellement (\(\Delta x=0\)) et avoir une quantité de mouvement bien définie (\(\Delta p=0\)), c’est-à-dire respecter l’égalité : \[\Delta x~\Delta p=0\]

En d’autres termes, les concepts mêmes de position (localisation) et de quantité de mouvement ne peuvent pas avoir, pour une particule quantique, strictement le même sens que pour une particule classique, ce qui n’empêche pas ces concepts, une fois refondus au moule quantique, de conserver toute leur importance.

Plus le domaine à explorer est petit, plus la quantité de mouvement maximale et donc l’énergie maximale de la particule doivent être grandes : d’où la nécessité d’accélérateurs de particules de plus en plus puissants.

Les accélérateurs actuels qui communiquent aux particules des énergies de quelques centaines de milliards d’électrons-volts rendent possible l’exploration des lois de la physique à l’échelle du millionième de milliardième de centimètre, soit \(10^{-15}\) centimètre.

Un deuxième type d’application du principe de Heisenberg concerne le problème fondamental de la physique atomique : comment expliquer la stabilité des atomes, l’existence d’un état d’énergie minimale ?

Prenons le cas de l’atome d’hydrogène. L’énergie totale de l’électron comportant deux termes, énergie cinétique et énergie potentielle, qui varient en sens inverse, trouve ainsi la possibilité d’être bornée inférieurement dans une région où ni l’un ni l’autre des deux termes ne l’emporte considérablement sur l’autre.

Ce raisonnement se formalise en écrivant l’énergie totale de la particule sous sa forme classique : \[E=\frac{p^2}{2~m}-\frac{e^2}{r}\qquad\text{r : distance électron - noyau}\]

Cette égalité étant soumise à la contrainte de la relation de Heisenberg \(p~r\geq h\), seule permettant l’utilisation simultanée des concepts approximativement classiques de position (\(r\)) et de quantité de mouvement (\(p\)).

On écrira donc : \[E~\geq~\frac{p^2}{2~m}-\frac{e^2}{r}\]

Le calcul montre que l’énergie admet un minimum pour une valeur de la distance entre l’électron et le noyau égale à \(r_0\) : \[r_0\approx\frac{h^2}{m~e^2}\qquad\Rightarrow\qquad E_0\approx-\frac{m~e^4}{h^2}\]

Expressions qui ne sont naturellement significatives qu’à un facteur numérique près.

2.2. Deuxième relation (temporelle) de Heisenberg

En parfaite analogie avec la relation de Heisenberg spatiale, on établit une relation de Heisenberg temporelle (une démonstration très commode - mais rigoureuse - existe en théorie du signal).

On note le fait classique qu’un phénomène de durée \(\Delta t\) ne peut être théorique qu’avec une approximation et que sa fréquence \(\nu\) ne peut avoir une valeur bien déterminée.

Le phénomène possède nécessairement une bande de fréquences de largeur \(\Delta \nu\) telle que \(\Delta t~\Delta\nu~\geq~1\). En introduisant l’énergie de la relation (1) de base, il vient : \[\Delta E~\Delta t~\geq~h\]

En physique quantique, seuls peuvent donc avoir des énergies bien déterminées (\(\Delta E=0\)) des systèmes permanents dans des états invariables au cours du temps (\(\Delta t=\infty\)): ce sont les états stationnaires. Inversement, des systèmes aux propriétés variables au cours du temps, dans des états non stationnaires, n’ont pas d’énergie bien déterminée.

Ainsi les états instables de divers systèmes physiques possèdent-ils une largeur d énergie naturelle minimale \(\delta E\), reliée à leur durée de vie \(\tau\) par la relation : \[\tau~\delta E~\geq~h\]

On a donc deux concepts absolument équivalents, durée de vie et largeur de la bande d’énergie. Seule la pratique expérimentale entraîne l’utilisation prioritaire de l’une ou de l’autre.

Considérons les désintégrations par interactions faibles des particules fondamentales, par exemple celle du méson \(\pi\) : \[\pi^+~\rightarrow~\mu^+ +\nu\]

Celles-ci ont des temps caractéristiques (durées de vie des particules) directement mesurables (\(\tau\approx 2,6\times 10^{-8}~\rm s\)) dans le cas cité, mais des largeurs très faibles d’énergie (\(\delta E\approx 2\times 10^{-14}~\rm MeV\)) par rapport à la masse du méson (\(m\approx 140~\rm MeV\)).

Au contraire, pour les désintégrations dues aux interactions fortes, par exemple : \[\rho^+~\rightarrow~\pi^++\pi^0\]

c’est la largeur du spectre d’énergie, ou spectre de masse, que l’on mesure directement (\(\delta E\approx 160~\rm MeV\)), car la durée de vie correspondante (\(\tau\approx 4\times 10^{-24}~\rm s\)) est beaucoup trop faible.