1. Construction géométrique du rayon réfracté

L’optique géométrique est l’étude de la propagation de la lumière en détectant la trajectoire des photons (rayons lumineux) émis par la source.

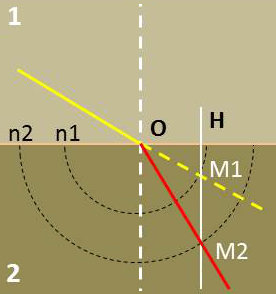On fait l’hypothèse que les indices de réfraction sont tels que \(n_2~>~n_1\).

À partir de O comme centre, on trace les cercles de rayons respectifs \(n_1\) et \(n_2\).

Le prolongement du rayon incident coupe le cercle \((n_1)\) en \(M_1\).

La perpendiculaire menée de \(M_1\) à la surface de séparation coupe le cercle \((n_2\)) en \(M_2\).

Le rayon réfracté est \(OM_2\).

En effet (triangles rectangles \(OHM_1\) et \(OHM_2\)) :

\[\begin{aligned} &OH~=~OM_1~\cos\widehat{HOM_1}~=~n_1~\sin(i_1)\\ &OH~=~OM_2~\cos\widehat{HOM_2}~=~n_2~\sin(i_2)\end{aligned}\]

On retrouve la formule de Snell-Descartes de l’article précédent.

2. Principe de Fermat

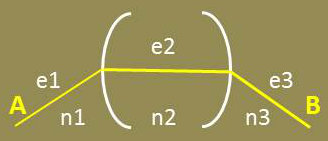Le principe de Fermat s’appuie sur la notion de chemin optique défini comme la distance qu’aurait parcourue la lumière dans le vide pendant la durée qu’elle met à effectuer le trajet dans le milieu donné : \[[AB]~=~n_1~e_1~+~n_2~e_2~+~n_3~e_3\]

Rappelons en effet que si \(n_i~=~c/v_i\) représente l’indice du milieu (i) par rapport au vide, on peut écrire (\(v_i\) vitesse de la lumière dans le milieu (i)) : \[n_i~e_i~=~\frac{c}{v_i}~e_i~=~c~\frac{e_i}{v_i}~=~c~t\]

Ce préliminaire étant fait, le principe de Fermat s’énonce :

Trajet optique. La lumière se propage d’un point à un autre sur des trajectoires telles que la durée du parcours soit stationnaire.

Ceci signifie que le trajet optique minimise localement (pour de petites variations) la durée du parcours. \[\delta(AB)~=~\delta\Big\{\int_A^Bn~ds\Big\}~=~0\]

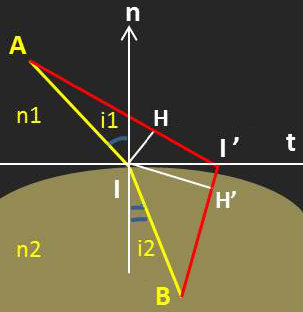Soit [AIB] le chemin suivi par le rayon lumineux et [AI’] un trajet fictif voisin (II’ très petit par rapport à AI et BI).

Pratiquement I’ est situé sur le vecteur \(\vec{t}\) tangent à la trajectoire (infiniment petits). On peut faire les approximations : \[AH\approx AI \qquad BH'\approx BI\]

On a successivement :

\[\begin{aligned} &[AI']~=~[AH]~+~[HI']\approx [AI]~+~n_1~\{II'\sin(i_1)\}\\ &[I'B]~=~[I'H']~+~[H'B]\approx n_2~\{II'\sin(i_2)\}+[IB]\end{aligned}\]

En additionnant membre à membre : \[[AI'B]~\approx~[AIB]~+~II'~\{n_1~\sin(i_1)~+~n_2~sin(i_2)\}~\approx~[AIB]\]

3. Théorème de Malus

On appelle surface d’onde le lieu des points d’égal chemin optique à partir de la source.

Le théorème de Malus s’énonce :

La surface d’onde est perpendiculaire au rayon lumineux en chacun de ses points.

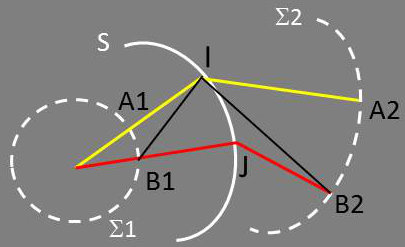Supposons la source située dans un milieu isotrope. La surface d’onde est alors une sphère \(\Sigma_1\).

Soit (S) la surface de séparation des milieux. Après la traversée de (S), la nouvelle surface d’onde sera \(\Sigma_2\).

Suivant la définition : \[[A_1IA_2]\approx [B_1JB_2]\]

Les points étant très voisins, on peut appliquer le principe de Fermat : \[[B_1JB_2]\approx [B_1IB_2]\]

Or : \[A_1I\perp \Sigma_1\qquad\text{(rayon/sphère)}\]

Donc: \[[B_1I]~=~[A_1I]\]

Par hypothèse : \[[A_1I]~+~[IA_2]~=~[B_1I]~+~[IB_2]\]

Il s’ensuit que : \[[IA_2]~=~[IB_2]\]

Mais \(B_2\) est arbitraire sur \(\Sigma_2\) ; ces deux longueurs ne peuvent être égales au second ordre près que si \(IA_2\) est orthogonal à \(\Sigma_2\). C’est ce qu’il fallait établir.

4. Construction de Huyghens

Dans un milieu (n), connaissant la surface d’onde \(\Sigma_1\) , on déduit \(\Sigma_2\) enveloppe des cercles de rayon \(r.n\) centrés sur \(\Sigma_1\).

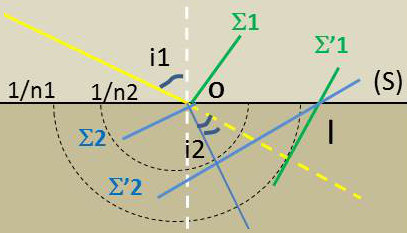
Dans la construction du rayon réfracté, les surfaces d’onde étant assimilées à des plans. Si le milieu (n) se prolongeait, l’onde \(\Sigma_1\) serait venue en \(\Sigma'_1\), coupant en I la surface de séparation (S) on aurait : \[OM_1\times n_1~=~1\] si on suppose qu’il s’est écoulé un temps \(t~=~1/c\).

Ce chemin optique doit être conservé dans le milieu [2], de sorte que si \(\Sigma'_2\) est la surface d’onde dans le deuxième milieu on a : \[OM_2\times n_2~=~1\] En effet : \[OM_2~=~v_2t=\frac{v_2}{c}~=~\frac{1}{n_2}\]

Comme au temps \(t~=~1/c\) l’onde \(\Sigma'_1\) aurait été en I, l’onde \(\Sigma'_2\) doit elle aussi passer par \(I\).

Construction

On trace les cercles de centre O et rayons respectifs : \[(O,R_1)~=~\frac{1}{n_1}\qquad ;\qquad (O,R_2)~=~\frac{1}{n_2}\]

La tangente en \(M_1\) donne le point \(I\).

À partir de \(I\), on trace la tangente au cercle de centre \(O\) et rayon \(R_2\)

Le rayon réfracté est obtenu en joignant \(OM_2\).

\[\begin{aligned} OM_1~=~OI~\cos\{\frac{\pi}{2}-i_1\}\qquad \text{soit}\qquad \frac{1}{n_1}~=~OI~\sin(i_1)\\ OM_2~=~OI~\cos\{\frac{\pi}{2}-i_2\}\qquad \text{soit}\qquad \frac{1}{n_2}~=~OI~\sin(i_2)\end{aligned}\]

D’où : \[\frac{1}{OI}~=~n_1~\sin(i_1)~=~n_2~\sin(i_2)\]

On retrouve bien la loi de Snell-Descartes.