1. Définitions

On appelle dioptre sphérique l’ensemble de deux milieux transparents, homogènes, d’indice différent, séparés par une surface sphérique.

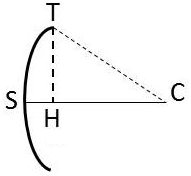Le centre C et le rayon r de cette surface sphérique s’appellent respectivement centre et rayon du dioptre. Généralement la surface sphérique est une calotte ; son pôle S est le sommet du dioptre.

La droite CS est l’axe principal ; toute droite passant par C et rencontrant la surface dioptrique est un axe secondaire. Tout plan passant par l’axe principal est une section principale. Le rayon d’ouverture du dioptre est le rayon du cercle de base de la calotte.

L’angle d’ouverture \(\theta\) est l’angle que fait avec l’axe principal un axe secondaire rencontrant le bord de la calotte.

2. Étude du stigmatisme

2.1. Recherche directe du stigmatisme

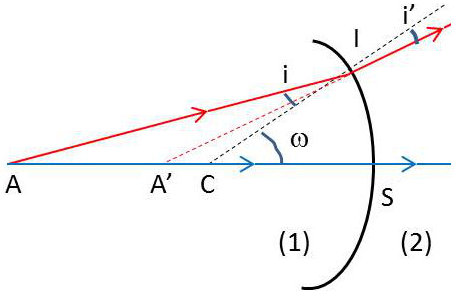Nous reprenons la même méthodologie que dans le cas du miroir sphérique à la différence près de la loi de Descartes qui est la loi de réfraction : \[n~\sin(i)~=~n'~\sin(i')\]

Il s’agit de voir si la position du point A’, image de A, dépend ou non du rayon incident AI utilisé. Pour abréger l’écriture, posons : \[\overline{CA}~=~z \quad;\quad \overline{CA'}~=~z' \quad;\quad \overline{CS}~=~\rho\]

Dans les triangles \(CIA\) et \(CIA'\) : \[\frac{z}{\sin(i)}=\frac{\overline{IA}}{\sin(\omega)} \quad; \quad \frac{z'}{\sin(i')}=\frac{\overline{IA'}}{\sin(\omega)}\]

D’où : \[\frac{z}{\overline{IA}~\sin(i)}=\frac{z'}{\overline{IA'}~\sin(i')}\]

Et suivant la relation de Descartes : \[\frac{n~z}{\overline{IA}}=\frac{n'~z'}{\overline{IA'}}\]

L’expression \(\cfrac{n~z}{\overline{IA}}\) est un invariant. Elle se conserve dans la réfraction.

2.2. Stigmatisme rigoureux

Il y aura stigmatisme rigoureux si z’ ne varie pas.

Il y a alors plusieurs solutions :

1) Lorsque \(z~=~z'~=~0\)  : Le dioptre est stigmatique pour son centre, ce qui était évident.

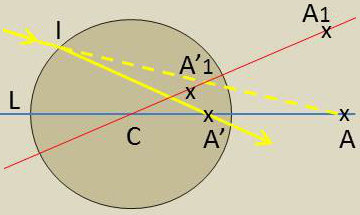
2) Lorsque \(\cfrac{\overline{IA'}}{\overline{IA}}\). Il suffit pour cela que le dioptre coïncide avec la sphère, lieu des points dont le rapport des distances aux points A et A’ est constant.

Soit \(LM\) le diamètre de cette sphère. La relation \[\frac{n~z}{\overline{IA}}=\frac{n'~z'}{\overline{IA'}}\] doit s’appliquer en particulier aux points L et M.

On devra donc avoir les deux relations :

\[\begin{aligned} &\frac{n~z}{r+z}=\frac{n'~z'}{r+z'}\\ &\frac{n~z}{r-z}=\frac{n'~z'}{z'-r}\end{aligned}\]

D’où : \[z=\frac{n'}{n}r \quad;\quad z'=\frac{n}{n'}r\]

Les points A et A’ ainsi définis sont les points de Young ou de Weierstrass. Le dioptre est rigoureusement stigmatique pour le point A dont il donne une image en A’.

Remarquons que cette propriété de stigmatisme se retrouve pour deux points \(A_1\) et \(A’_1\) situés sur un axe secondaire quelconque passant par C, à condition que leurs distances à C soient z et z’.

2.3. Stigmatisme approché. Approximation de Gauss.

Il y aura stigmatisme approché si le rapport IA/IA’ ne varie pas de façon notable. Ce sera en particulier le cas lorsque IA et IA’ sont simultanément stationnaires, c’est-à-dire lorsque le point I se trouve au voisinage du sommet S du dioptre.

On est alors dans l’approximation de Gauss que nous allons maintenant étudier.

Nous partons de : \[\frac{n~z}{\overline{IA}}=\frac{n'~z'}{\overline{IA'}}\]

La relation de conjugaison (avec origine au centre) s’en déduit en faisant : \[IA~=~z~+~r \qquad IA'~=~z'~+~r\]

On trouve ainsi : \[\frac{1}{n}~\left\{\frac{1}{z}+\frac{1}{r}\right\}=\frac{1}{n'}~\left\{\frac{1}{z'}+\frac{1}{r}\right\}\]

Cette formule est très utile lorsque l’on a à étudier une famille de dioptres concentriques, mais nous utiliserons plus souvent la relation avec origine au sommet. On fera alors le changement de variable : \[IA=x \quad;\quad IA'=x' \quad;\quad z=x-r \quad;\quad z'=x'-r\]

On obtient alors : \[n~\left\{\frac{1}{r}-\frac{1}{x}\right\}=n'~\left\{\frac{1}{r}-\frac{1}{x'}\right\}\]

On voit que la quantité  \(n~\bigg\{\cfrac{1}{r}-\cfrac{1}{x}\bigg\}\)  est invariante à la réfraction sur un dioptre.

On écrit souvent la relation de conjugaison sous la forme : \[\frac{n'}{x'}-\frac{n}{x}~=~\frac{n'-n}{r}\]

En conclusion un dioptre sphérique donne d’un point A situé sur un axe secondaire AC une image A’ dont la position est fixée par la précédente relation (à condition de se limiter aux rayons qui font un petit angle avec AC).

3. Image d’un petit objet plan dans un dioptre de faible ouverture

Le raisonnement effectué pour les miroirs sphériques est applicable ici :

Un dioptre sphérique de faible ouverture donne d’un petit objet plan, perpendiculaire à son axe et centré sur lui, une image satisfaisante (stigmatisme approché) qui est plane, perpendiculaire à l’axe et centrée sur lui, à condition que les rayons des pinceaux que les divers points de l’objet envoient sur le dioptre le frappent sous une incidence faible (rayons centraux).

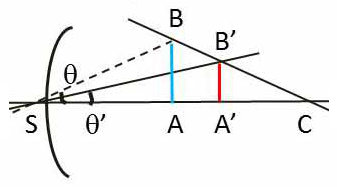Les plans de front, objet P et image P’, sont des plans conjugués ; leurs points de rencontre A et A’ avec l’axe sont deux points conjugués dont les positions sur cet axe sont liés par la relation de conjugaison.

L’image est homothétique de l’objet par rapport au point C, centre du dioptre. On aura donc : \[\gamma~=~\frac{z'}{z}\]

On peut encore exprimer \(\gamma\) en fonction de x et x’ en utilisant le rayon BSB’ : \[\frac{y'}{y}~=~\frac{\theta'x}{\theta x}~=~\frac{n}{n'}~\frac{x'}{x}\]

4. Origine au sommet du dioptre. Foyers

Reprenons la relation de correspondance objet image : \[\frac{n'}{x'}-\frac{n}{x}~=~\frac{n'-n}{r}\]

C’est une relation homographique : à chaque position d’un point objet A correspond une position et une seule pour le point image A’.

Mettons en évidence quelques positions particulièrement importantes des points objet et image.

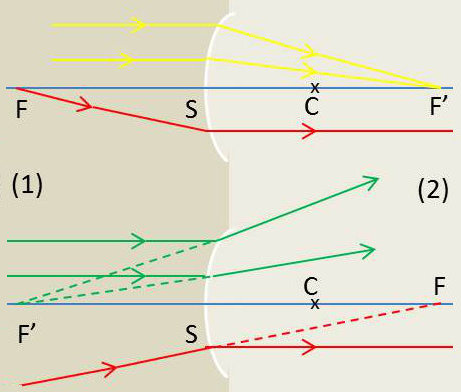1) \(x~=~r \quad\Rightarrow\quad x'~=~r\) ;

Nous retrouvons le centre qui est à lui-même son image. Tout rayon dont le support passe par C, traverse le dioptre sans déviation.

2) Lorsque A est à l’infini A’ est en F’ :

Son abscisse \(\overline{SF'}~=~f'\) s’obtient en faisant \(x~=~\infty\) dans la relation : \[f'=\frac{n'}{n'-n}~r\]

F’ est le foyer image et f’ est la distance focale image.

À tout incident parallèle à l’axe correspond donc un réfracté dont le support passe par F’.

Si F’ est réel, le dioptre recevant un faisceau parallèle à son axe le transforme en un faisceau convergent. Il est dit convergent.

Si F’ est virtuel le dioptre transforme en un faisceau divergent un faisceau parallèle à son axe. Il est dit divergent.

3) Il existe une position particulière F du point objet pour laquelle le point image est à l’infini. F s’appelle le foyer objet et son abscisse est la distance focale objet. Elle est donnée par la relation homographique dans laquelle on fait. On obtient alors : \[f~=~\frac{n}{n-n'}~r\]

Tout rayon incident dont le support passe par F se réfracte parallèlement à l’axe.

Remarques

1) Les deux distances focales sont de signes contraires, les foyers sont donc de part et d’autre de S, ils sont simultanément réels ou simultanément virtuels.

2) Choisissons comme sens positif sur l’axe le sens de la lumière réfractée (sens de la lumière à la sortie du système optique). C’est aussi le sens de la lumière incidente. Nous aurons une condition de convergence en écrivant que \(f'>0\) : \[\frac{n'}{n'-n}~r~>~0 \qquad \text{ou} \qquad \frac{r}{n'-n}~r~>~0\]

C’est-à-dire que r doit être du signe de (n’ - n) ou encore que le centre doit être dans le milieu le plus réfringent.

3) Des formules donnant les expressions des distances focales nous déduisons : \[\frac{f}{f'}~=-~\frac{n}{n'}\]

Le rapport des distances focales est égal au rapport changé de signe des indices des milieux correspondants.

4) Cherchons le milieu de FF’. En formant pour cela la somme des distances focales, on trouve que \(f~+~f'~=~r\) . On en déduit que les milieux de FF’ et de SC coïncident. Nous avons vu que les foyers sont de part et d’autre de S, celui qui est du côté opposé à C par rapport à S étant nécessairement en dehors de SC, il en est de même de l’autre foyer. Aucun foyer ne peut donc se trouver entre S et C. De plus : \[\overline{SF}~=~-\overline{CF'}\qquad\text{et}\qquad \overline{SF'}~=~-\overline{CF}\]

Ce sont des particularités à prendre en compte lorsque, dans les figures se rapportant au dioptre sphérique, on veut placer les foyers après avoir marqué le sommet S et le centre C.

5) Si on multiplie les deux membres de l’équation de conjugaison par \(r/(n'-n)\), celle-ci prend la forme simple suivante : \[\frac{f'}{x'}+\frac{f}{x}~=~1\]

Elle ne contient plus les indices des deux milieux réfringents, ni le rayon du dioptre.

5. Plans focaux

Les plans focaux sont les plans de front passant par les foyers.

• Le plan focal objet a pour image le plan perpendiculaire à l’axe situé à l’infini.

• Le plan focal image est l’image du plan de front à l’infini.

• Les plans focaux d’un dioptre sphérique convergent sont réels.

• Dans un dioptre sphérique divergent les plans focaux sont virtuels.

6. Constructions géométriques

6.1. Rayon réfracté correspondant à un incident donné

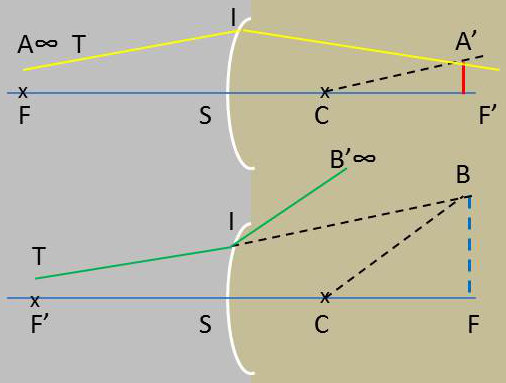On utilise les propriétés du centre et des plans focaux :

a) Soit TI le rayon incident. Admettons qu’il provienne du point A placé à l’infini sur son support. Le rayon réfracté passera par A’ image de A dans le dioptre.

Cette image A’ est dans le plan focal image, à l’intersection de ce plan avec l’axe secondaire qui passe par A (parallèle à TI menée par C).

Le rayon réfracté est donc IA’.

b) Voici une deuxième construction. Pour varier, nous faisons la figure en supposant le dioptre divergent. Le rayon incident TI perce le plan focal objet en un point B dont l’image B’ est à l’infini sur CB. Le réfracté devant passer par B’ s’obtient en menant par I la parallèle à CB.

Les constructions précédentes ne sont valables que dans l’approximation de Gauss. Au contraire, la construction qui utilise les points de Weierstrass n’implique aucune hypothèse sur les conditions dans lesquelles le dioptre travaille.

6.2. Construction de l’image d’un objet

6.2.1. Plan objet à l’infini

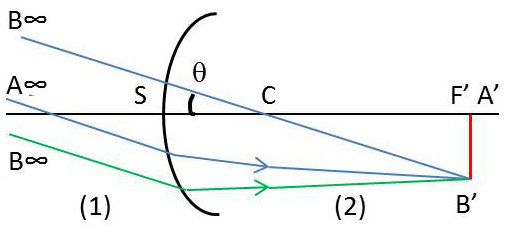
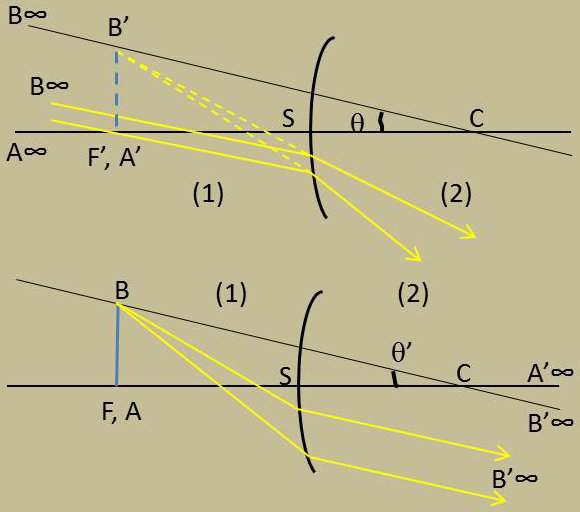L’image du plan objet à l’infini est dans le plan focal image.

Le point A sur l’axe a son image A’ en F’.

Un point B en dehors de l’axe et dont la distance angulaire à A est \(\theta\) a son image au point d’intersection B’ du plan focal image et de l’axe secondaire BC.

Si le dioptre est convergent, son image est réelle et renversée.

Si le dioptre est divergent, son image est droite et virtuelle.

Dans les deux cas nous avons : \[A'B'=CF'.\theta=-SF.\theta=-f.\theta\]

6.2.2. Plans objet et focal objet en coïncidence

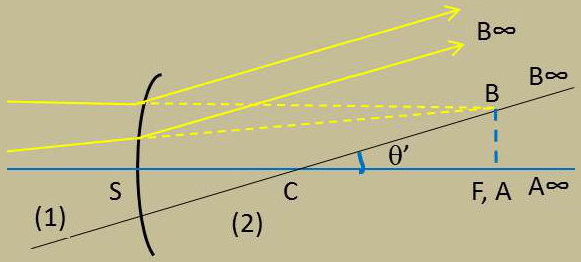Quand les plans objet et focal sont en coïncidence, leur image commune est le plan de front à l’infini. Le point A sur l’axe a son image A’ à l’infini sur cet axe.

Un point B en dehors de l’axe a son image B’ à l’infini sur CB ; la distance angulaire des points A’ et B’ est : \[\theta'~=~\frac{AB}{CF}~=~\frac{AB}{SF'~}=~\frac{AB}{f'}\]

L’image est renversée si le dioptre est convergent, droite si le dioptre est divergent.

6.2.3. Position de l’objet quelconque

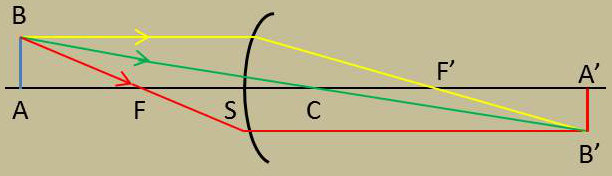La construction de l’image d’un objet se fait sans difficulté.

On raisonne comme dans le cas des miroirs sphériques et on utilise deux quelconques des rayons particuliers suivants :

• le rayon incident passant par le foyer objet qui se réfracte parallèlement à l’axe ;

• le rayon incident qui se réfracte en passant par le foyer image ;

• le rayon incident passant par le centre et qui n’est pas dévié.

(Construction du schéma : dioptre convergent et objet réel situé dans le milieu le moins réfringent).

7. Formules du dioptre sphérique

Rappelons pour mémoire les premières formules établies pour le stigmatisme approché avec origine au centre et la formule du grandissement linéaire : \[n~\bigg\{\frac{1}{z}+\frac{1}{r}\bigg\}~=~n'~\bigg\{\frac{1}{z'}+\frac{1}{r}\bigg\}\qquad~; \qquad \frac{y'}{y}~=~\frac{z'}{z}\]

Notons que l’on utilise en fait plus fréquemment les formules de Descartes (origine au sommet) que les formules de Newton (origine aux foyers).

7.1. Origine au sommet (formules de Descartes)

Posons : \[\overline{SA}~=~x\quad;\quad \overline{SA'}~=~x'\quad;\quad \overline{SC}~=~r\]

Il vient : \[\frac{n'}{x'}-\frac{n}{x}~=~\frac{n'-n}{r}\qquad~; \qquad \frac{y'}{y}~=~\frac{n'}{n}~\frac{x'}{x}\]

En faisant \(r=\infty\), on retrouve les formules du dioptre plan.

7.2. Origine double aux foyers (formules de Newton)

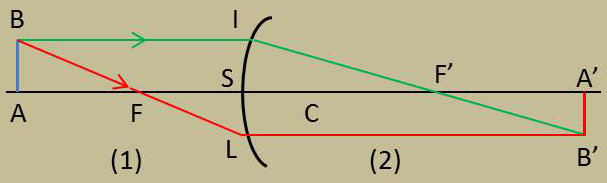Nous allons rapporter la position du plan objet au foyer objet F et fixer la position du plan image par rapport au foyer image F’. Posons donc : \[\overline{FA}=\sigma\quad;\quad \overline{FA'}=\sigma'\]

Il est entendu que les segments SF et SF’ représentent respectivement la distance focale objet et la distance focale image du dioptre.

Par hypothèse les arcs SI et SL sont assez petits pour que l’on puisse les confondre avec la perpendiculaire à l’axe menée par S.

La similitude des triangles A’B’F’ et SIF’ nous donne, en remarquant que \(SI = AB = y\) : \[\gamma~=~\frac{y'}{y}~=~-\frac{\sigma'}{f'}\]

Avec les triangles ABF et FSL : \[\gamma~=~\frac{y'}{y}~=~-\frac{f}{\sigma'}\]

On en déduit (conjugaison) : \[\sigma~\sigma'~=~f~f'\]

Remarques

1) \(f\) et \(f'\) étant de signes contraires, \(\sigma~\sigma'<0\), donc ces deux paramètres sont aussi de signes contraires.

2) Différentions la relation de Newton : \[\sigma~d\sigma'+\sigma'~d\sigma~=~0 \quad\Rightarrow\quad \frac{d\sigma'}{d\sigma}~=~-\frac{\sigma'}{\sigma}\]

Les deux éléments différentiels sont donc de même signe. Donc le plan objet et le plan image se déplacent dans le même sens. Ils se rencontrent d’ailleurs deux fois : en C et en S.

Le rapport \(\gamma_x=d\sigma'/d\sigma\) est le grandissement axial pour les points conjugués A et A’.

3) Puisque \(\gamma=-f\sigma\), nous voyons que :

• à chaque valeur de \(\sigma\) correspond une valeur et une seule pour \(\gamma\), donc à chaque position du plan objet correspond une valeur parfaitement déterminée de \(\gamma\) et inversement ;

• quand l’objet se déplace, occupant sur l’axe toutes les positions possibles, le grandissement linéaire prend une seule fois toute valeur \(\in\{-\infty,+\infty\}\).

8. Formules de Lagrange-Helmoltz

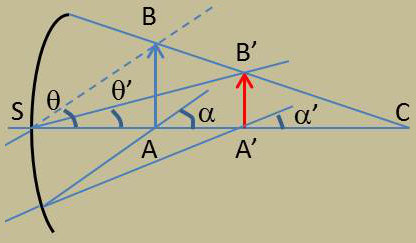La formule que nous allons établir dans le cas des dioptres peut être traitée de manière identique dans le cas des miroirs.

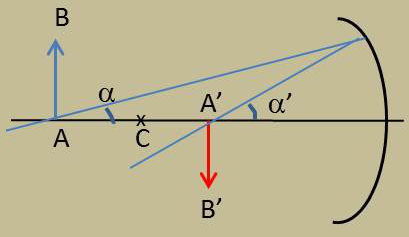
Soit AB un objet, A’B’ son image, \(\alpha\) et \(\alpha'\) les angles que font les rayons IA et IA’ avec l’axe.

On a dans les triangles SAI et SA’I : \[SI~=~-\alpha~x~=~-\alpha'~x\]

Par ailleurs (grandissement) : \[\frac{y'}{y}~=~\frac{n'}{n}~\frac{x'}{x}\]

En éliminant x et x’ : \[n~y~\alpha~=~n~y~\alpha'\]

C’est la relation de Lagrange-Helmoltz.

La quantité \(ny\alpha\) est donc invariante dans la réfraction. On verra qu’elle joue un rôle très important dans l’étude générale des systèmes centrés.

Il serait aussi facile d’établir que dans les miroirs on a une relation analogue, mais avec un changement de signe : \[y~\alpha~=~-y'~\alpha'\]