1. Quelques définitions

Les réseaux sont des dispositifs qui, par un jeu d’interférences, permettent d’obtenir une dispersion de la lumière, comme le font les prismes. Mais les réseaux possèdent sur les prismes un certain nombre d’avantages qui font qu’ils peuvent supplanter les prismes dans la plupart des applications spectroscopiques.

D’une façon générale, un réseau est une surface transparente ou réfléchissante sur laquelle on a réalisé une perturbation périodique (suivant une dimension) de transparence ou de réflexion, à pas très serrés et comportant un grand nombre de pas.

Le pas du réseau varie entre une fraction de micromètre et plusieurs dizaines de micromètres. Le nombre total de pas ou de sillons est de l’ordre de plusieurs milliers (voire jusqu’à quelques centaines de milliers).

2. La théorie du réseau illimité

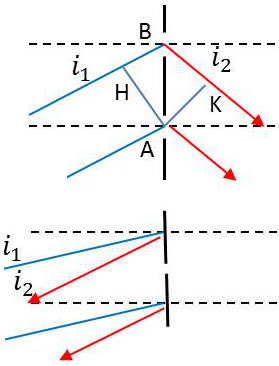Soient deux perturbations \(A\) et \(B\) consécutives du réseau et \(a\) le pas du réseau. La figure 1 représente un réseau par transmission et la figure 2 un réseau par réflexion.

Les angles \(i_1\) et \(i_2\) sont orientés positivement quand le sens est trigonométrique. Dans le cas de la figure 1 : \(i_1>0\) et \(i_2<0\).

Calculons la différence de marche entre deux rayons consécutifs (calcul et résultat identiques dans le deux cas) :

\[\begin{aligned} &\delta=\overline{HB}+\overline{BK}=\overrightarrow{n_1}\cdot\overrightarrow{AB}+\overrightarrow{n_2}\cdot\overrightarrow{BA}\\ &\delta=(\overrightarrow{n_1}-\overrightarrow{n_2})\cdot\overrightarrow{AB}\end{aligned}\]

Or, on a :

\[\begin{aligned} &\overrightarrow{n_1}\cdot\overrightarrow{AB}=\cos\big(\frac{\pi}{2}-i_1\big)\\ &\overrightarrow{n_2}\cdot\overrightarrow{AB}=\cos\big(\frac{\pi}{2}-i_2\big)\end{aligned}\]

Par suite : \[\delta=a~\{\sin(i_1)-\sin(i_2)\}\]

Remarque 1

Il existe une manière simple d’écrire \(\delta\) dans tous les cas de figure :

– Si le rayon incident et le rayon réfracté sont d’un même côté de la normale : \[\delta=a~\{\sin(i_1)-\sin(i_2)\}\]

– Si ces rayons sont de part et d’autre de la normale : \[\delta=a~\{\sin(i_1)+\sin(i_2)\}\]

Remarque 2

S’il y a n traits par unité de longueur, le pas du réseau est \(a=\dfrac{1}{n}\) et par suite : \[\delta=\frac{1}{n}~\{\sin(i_1)-\sin(i_2)\}\]

2.1. Recherche des maximums

Si \(\delta\neq K\lambda\) si peu que ce soit, l’interférence est totalement destructive. En effet, le nombre d’éléments étant illimité et la différence de marche entre rayons ayant passé par deux éléments séparés par \(m\) intervalles étant \(m\delta\), on peut alors associer à chaque rayon un autre rayon en opposition de phase avec lui, et l’interférence de l’ensemble est destructive.

L’interférence sera constructive si l’on a : \[\varphi=2K\pi=\frac{2\pi}{\lambda}~\delta\qquad\Rightarrow\qquad\delta=K~\lambda\]

On observe des maximums de lumière et, en dehors de ces maximums, il n’y a aucune lumière. Les maximums sont donc infiniment fins, ce qui provient du fait que le réseau est illimité.

2.2. Distribution des maximums

Plaçons-nous dans le cas où \(i_1>0\) et \(i_2>0\) et supposons pour simplifier que : \[\sin(i_1)+\sin(i_2)=n~K~\lambda\]

L’angle \(i_1\) étant donné, l’angle \(i_2\) sera déterminé par : \[\sin(i_2)=n~K~\lambda-\sin(i_1)\]

\(K\) prenant des valeurs entières, positives et négatives, \(\sin(i_2)\) prendra des valeurs symétriques par rapport à [\(-\sin(i_1)\)] .

On remarquera cependant que les valeurs de \(i_2\) ne sont pas symétriques par rapport à \(i_1\), sauf si \(i_1=0\).

Le nombre des maximums est limité, car : \[|\sin(i_2)|<1\qquad\Rightarrow\qquad |n~K~\lambda-\sin(i_1)|<1\]

Pour une longueur d’onde donnée \(\lambda\), le nombre de maximums est d’autant plus petit que \(n\) est plus grand. Il peut même arriver qu’aucun maximum (\(K\neq 0\)) n’existe si l’équation n’est pas vérifiée pour : \[K=1\quad;\quad n~\lambda>1+\sin(i_1)\]

Si l’on opère en incidence rasante, la longueur d’onde maximale pour laquelle un réseau peut être utilisé est : \[n~\lambda_m=2\quad;\quad \lambda_m=\frac{2}{n}=a\]

Ainsi les réseaux pour l’infrarouge ont-ils un pas moins serré que pour le visible.

2.3. Dispersion

La formule fondamentale montre que les positions des maximums dépendent de \(\lambda\) (sauf pour la valeur de \(K=0\)). Il y a une dispersion et, comme les maximums sont infiniment fins, on pourra ainsi séparer les radiations.

Si on éclaire en lumière polychromatique, le maximum central (pour \(K=0\)) ne sera pas dispersé, mais les autres donneront des spectres d’ordre \([\dots, -2, -1, +1, +2, \dots]\).

L’aptitude d’un réseau à produire cette dispersion est caractérisée par sa dispersion angulaire : \[D=\frac{di}{d\lambda}\quad;\quad i_1=cte\]

En différentiant l’équation fondamentale : \[\cos(i_2)di_2=n~K~d\lambda\qquad\Rightarrow\qquad D=\frac{di_2}{d\lambda}=\frac{n~K}{\cos(i_2)}\]

Mais \(K\) et \(n\) sont liés, on a donc intérêt à revenir à la formule : \[\sin(i_1)+\sin(i_2)=n~K~\lambda\qquad\Rightarrow\qquad D=\frac{1}{\lambda}~\frac{\sin(i_1)+\sin(i_2)}{\cos(i_2)}\]

Cette formule montre que la dispersion ne dépend en fait que des angles sous lesquels le réseau est utilisé. Une condition de travail avantageuse est celle pour laquelle \(i_2=0\). On dit alors qu’on travaille en dispersion normale et qu’on obtient un spectre normal.

2.4. Pouvoir de résolution théorique

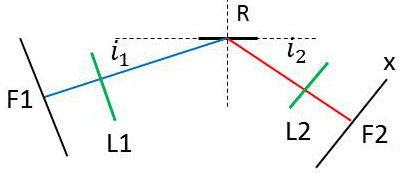Supposons que le réseau soit éclairé par une fente infiniment fine placée dans le plan focal d’une lentille collimateur. Dans ce cas, les maximums d’interférence sont infiniment fins.

Considérons maintenant deux longueurs d’onde aussi voisine qu’on le veut : \(\lambda\) et \(\lambda+d\lambda\) .

Elles donnent, dans le plan focal d’une lentille \(L_2\) placée après le réseau deux images infiniment fines qui seront toujours séparées, si petite que soit leur distance : \[dx=f~di_2=f~D~d\lambda\]

Il ne s’agit là que d’un pouvoir de résolution théorique parce que la fente source est infiniment fine et que le réseau est illimité. C’est la raison pour laquelle nous trouvons un pouvoir de résolution infini. Nous verrons que la question est plus délicate dans le cas d’une fente de largeur déterminée et d’un réseau fini.

2.5. Superposition des ordres

Donnons-nous \(i_1\) et \(i_2\)  ; dans la direction \(i_2\), il y aura des maximums d’interférence pour toutes les longueurs d’onde satisfaisant à la relation : \[\sin(i_1)+\sin(i_2)=n~K~\lambda_k\]

En chaque point du plan focal de \(L_2\) viendront se focaliser, non pas une radiation, mais une série de radiations répondant à la relation : \[\lambda_1=2~\lambda_2=3~\lambda_3=\dots\]

Soit, avec le nombre d’onde \(\sigma=\cfrac{1}{\lambda}\) : \[\sigma_1=\frac{\sigma_2}{2}=\frac{\sigma_3}{3}=\dots=\frac{\sigma_k}{k}\]

On peut donc définir un intervalle spectral libre : \[\Delta\sigma=\sigma_{k+1}-\sigma_k\]

Si la lumière qui éclaire le réseau ne contient pas de radiations en dehors de l’intervalle \(\Delta\sigma\), on est certain de ne pas avoir de mélanges ou de superpositions de raies des divers ordres \(K\). Compte tenu des relations précédentes, on a : \[\Delta\sigma=\sigma_1=\frac{\sigma_k}{K}=\frac{n}{\sin(i_1)+\sin(i_2)}\]

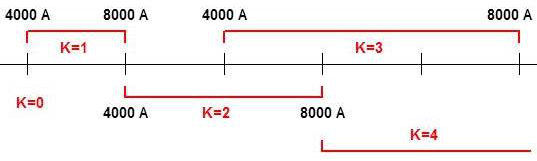Ainsi, \(\Delta\sigma\) dépend de \(i_1\) et \(i_2\) et il est d’autant plus large que le réseau est plus serré. En lumière blanche, on a le schéma représenté ci-contre.

Ces superpositions d’ordres présentent surtout des inconvénients. On peut y remédier par l’insertion de filtres sur le trajet de la lumière. Souvent d’ailleurs, la sensibilité sélective du récepteur (œil, plaque photographique, etc.) diminue d’elle-même certaines superpositions.

3. Théorie du réseau limité

Supposons maintenant que le réseau comporte un nombre fini N de traits. Entre deux traits consécutifs, et en supposant que les rayons soient situés du même côté de la normale : \[\delta=a~\{\sin(i_1)+\sin(i_2)\}\]

3.1. Intensité diffractée

Le déphasage entre deux rayons consécutifs étant \(\varphi=\dfrac{2\pi}{\lambda}~\delta\), les amplitudes diffractées successives ont pour expressions (du trait 1 au trait N): \[A_0~~;~~A_0\exp(-j\varphi)~~;~~A_0\exp(-j2\varphi)~~;~~\dots~~;~~A_0\exp[(-j(N-1)\varphi)]\]

L’amplitude totale diffractée sera : \[A=A_0\{1+\exp(-j\varphi)+\exp(-j2\varphi)+\dots+exp[-j(N-1)\varphi]\}\]

On est conduit de manière classique à rechercher la somme des premiers termes d’une progression géométrique de raison \(q=\exp(-j\varphi)\) et de premier terme \(a\), c’est à dire : \[S_N=a~\frac{1-q^N}{1-q}\]

Soit ici :

\[\begin{aligned} &A=A_0~\frac{1-\exp(jN\varphi)}{1-\exp(j\varphi)}\\ &A=A_0~\frac{\exp(jN\varphi/2)}{\exp(j\varphi/2)}\cdot\frac{\exp(-jN\varphi/2)-\exp(+jN\varphi/2)}{\exp(-j\varphi/2)-\exp(+j\varphi/2)}\end{aligned}\]

On a donc:

\[\begin{aligned} &A=A_0~\exp\left(j\frac{N-1}{2}\varphi\right)~\frac{\sin(N\varphi/2)}{\sin(\varphi/2)}\\ &A^*=A_0^*~\exp\left(j\frac{1-N}{2}\varphi\right)~\frac{\sin(N\varphi/2)}{\sin(\varphi/2)}\\ &AA^*=A_0A_0^*~\frac{\sin^2(N\varphi/2)}{\sin^2\varphi/2}\end{aligned}\]

D’où : \[I=I_0~\frac{\sin^2(N\varphi/2)}{\sin^2(\varphi/2)}\]

3.2. Maximums principaux et secondaires

On sait que \(cfrac{\sin(u)}{u}=0\) quand \(u=0\). Dans ce cas, on a \(I=I_0\) et l’on dit alors que l’on a un maximum principal : \[\varphi/2=K\pi\quad\Rightarrow\quad\varphi=2K\pi\quad\Rightarrow\quad\delta=K\lambda\]

Alors le maximum principal obtenu est dit d’ordre \(K\).

Étudions à présent la variation de l’intensité entre deux maximums principaux en faisant varier \(\varphi\) entre \(2K\pi\) et \((2K\pm 1)\pi\).

Posons : \(\varphi=2K\pi+\varepsilon~~~;~~~[-\pi<\varepsilon<+\pi]\). \(\varepsilon\) est supposé aussi petit que l’on veut, mais sans que \(N\varepsilon\) le soit.

L’intensité s’annule lorsque : \[N\varepsilon=2\pi\quad\Rightarrow\quad\varepsilon=2\pi/N\]

Le maximum principal d’ordre \(K\) est suivi d’un minimum nul, atteint lorsque la différence de phase entre deux vibrations diffractées par deux traits consécutifs est \((2K\pi+2\pi/N)\), c’est-à-dire lorsque la différence de marche est : \[\delta=K\lambda+\lambda/N\]

Le maximum principal suivant est obtenu pour la valeur \(\delta=K\lambda+\lambda\).

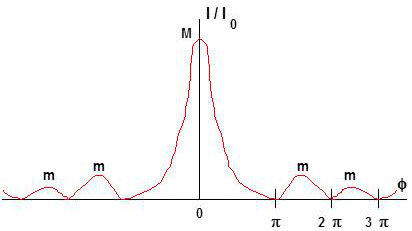On voit donc qu’il y a (N – 1) minimums nuls entre deux maximums principaux.

Deux minima nuls consécutifs sont séparés par un maximum secondaire m.

Entre deux maximums principaux, il y a (N – 2) maximums secondaires.

La figure ci-contre représente la variation de l’intensité au voisinage du maximum M d’ordre \(K=0\).

Largeur d’un maximum

Quand on passe d’un maximum à l’autre, la distance est \(\delta=\lambda/N\).

L’angle d’incidence \(i_1\) étant fixé, nous cherchons le \(\delta i_2\) qui donnera la largeur angulaire du maximum :

\[\begin{aligned} \Delta&=a~\{\sin(i_1)+\sin(i_2)\}\\ d\Delta&=a~\cos(i_2)~di_2=\frac{\lambda}{N}\\ \Rightarrow\quad\delta i_2&=\cfrac{\lambda}{N~a~\cos(i_2)}\end{aligned}\]

Remarquons que \(Na = L\) est la largeur totale du réseau.

Si l’on observe le phénomène dans le plan focal d’une lentille, on a : \[dx=f~di_2\]

Ce calcul peut être fait pour les maximums secondaires. Il suffira de remarquer sur la courbe que le maximum principal est deux fois plus large que les autres.

3.3. Pouvoir de résolution du réseau

Pour définir le pouvoir de résolution théorique du réseau, nous supposerons que celui-ci est éclairé par une source fente infiniment fine placée dans le plan focal d’un collimateur.

Pour que les maximums correspondant à deux longueurs d’onde voisines \(\lambda\) et \(\lambda'=\lambda+d\lambda\) soient résolus, il faut que leur distance angulaire \(di_2\) soit au moins égale à \(\delta~i_2\).

Reprenons la relation : \[a~\{\sin(i_1)+\sin(i_2)\}=K~\lambda\]

En différentiant :

\[\begin{aligned} a~\cos(i_2)~di_2&=K~d\lambda\\ \Rightarrow\qquad\qquad di_2&=\frac{K~d\lambda}{a~\cos(i_2)}\end{aligned}\]

En écrivant ensuite que \(di_2=\delta~i_2\), le pouvoir séparateur ou pouvoir de résolution sera : \[R=\frac{\lambda}{d\lambda}=K~N\]

Remarque 1

Il y a en fait un certain danger dans l’application de cette formule, car \(N\) et \(K\) ne sont pas complètement indépendants : \[a~\{\sin(i_1)+\sin(i_2)\}=K~\lambda\]

Ou encore : \[N~a~\{\sin(i_1)+\sin(i_2)\}=N~K~\lambda\]

Le pouvoir de résolution ne dépend que de la largeur \(Na\) du réseau et des angles d’utilisation.

Remarque2

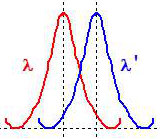On peut procéder plus simplement pour le calcul de \(R\) en remarquant que \(\lambda\) et \(\lambda'=\lambda+d\lambda\) sont juste séparées lorsque le maximum principal de l’une coïncide avec le premier minimum nul de l’autre.

Pour l’une : \(\Delta'=N~K~\lambda'+\lambda'\)

Pour l’autre : \(\Delta=N~K~\lambda\)

Opérant dans la même direction \(i_2\), ceci entraine \(\Delta'=\Delta\), donc :

\[\begin{aligned} &N~K~\lambda'+\lambda'=N~K~\lambda\\ &\lambda'=N~K~(\lambda-\lambda')~\delta\lambda~N~K\end{aligned}\]

Mais \(\lambda\approx\lambda'\), ce qui fait que : \[R=\frac{\lambda}{\delta\lambda}=N~K\]

3.4. Influence de la largeur de la fente

Le réseau à fentes est un réseau de transmission. Si la fente est infiniment fine, nous pouvons supposer que chaque fente produit dans une direction quelconque une vibration d’amplitude constante.

Ce n’est pas rigoureusement correct, car si l’on tient compte de la largeur \(b\) de la fente, il y a pour chaque motif une intensité diffractée : \[I=I_0~\frac{\sin^2(u)}{u^2}=I_0~\operatorname{sinc}^2(u)\quad;\quad u=\frac{\pi\delta_1}{\lambda}\]

Enfin il faut prendre en considération le terme réseau qui est un terme d’interférence : \[\frac{\sin^2(N\varphi/2)}{\sin^2(\varphi/2)}\quad;\quad\varphi=\frac{2\pi}{\lambda}~\delta_2\]

On a alors : \[I_1=I_0~\operatorname{sinc}^2\big(\frac{\pi\delta_1}{\lambda}\big)\cdot\frac{\sin^2(N~\pi~\delta_2/\lambda)}{\sin^2(\pi~\delta_2/\lambda)}\]