1. Introduction
Les applications des interférences sont multiples. On a eu l’occasion de parler des expériences de Michelson et de Fizeau préliminaires à la théorie de la relativité.
Nous décrirons ici quelques applications très simples.
2. Mesure de l’indice d’un gaz
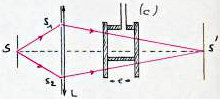 Nous avons schématisé ici la méthode de Rayleigh.
Nous avons schématisé ici la méthode de Rayleigh.
C’est une cuve dont on a prolongé volontairement les bords en verre de sorte que lorsque \(C\) est pleine d’air, la différence de marche en \(S'\) soit nulle.
On observe une frange brillante.
Si on fait le vide dans la cuve, l’indice de l’air étant \(n\), l’épaisseur de cuve étant \(e\), on crée une différence de marche entre \(S_1S'\) et \(S_2S'\) : \[\delta=n~e-e=(n-1)~e\]
Des franges défilent en \(S'\), une frange arrivant avec chaque \(\lambda\).
Ce nombre de franges est : \[p=\frac{\delta}{\lambda}=\frac{(n-1)~e}{\lambda}\]
Si la cuve est remplie par un gaz \(n'\) on aura une différence de marche : \[\delta=(n'-n)~e\]
Ou encore, en supposant que \(n=1\) pour l’air : \[\delta=(n'-1)~e\]
Ce dispositif est utilisé pour mesurer l’indice d’un gaz et ses variations en fonction de la pression et de la température.
On a pu ainsi établir que \((n – 1)\) est proportionnel à \(\rho\), masse volumique du gaz. Pour un gaz parfait : \[n-1=\frac{K~\rho}{T}\]
Remarque
On peut réaliser la même expérience avec les interféromètres à faisceaux séparés. Il suffit de placer la cuve sur le trajet de l’un des faisceaux en faisant bien attention de compenser sur l’autre faisceau l’épaisseur des parois de verre de la cuve.
3. Aérodynamique. Étude en soufflerie
 On peut étudier le profil \(P\) d’une aile d’avion à l’aide de l’interféromètre de Mach Zender.
On peut étudier le profil \(P\) d’une aile d’avion à l’aide de l’interféromètre de Mach Zender.
Il suffit de connaître la répartition des pressions autour de l’obstacle, sachant que : \[n=1+0,0003\frac{P}{P_0}\qquad P_0~:\text{ pression atmosphérique}\]
On étudie la distribution de l’indice (l’épaisseur de l’air est connue et constante).
En orientant convenablement \(M_1\) et \(L_2\), la région de localisation des franges se situe entre \(M_1\) et \(L_2\) où on place l’objet à étudier.
L’observation se fait à travers deux fenêtres \(A\) et \(B\) formées par deux lames à faces parallèles de très haute qualité.
4. Mesure de différence de marche introduite par une lame mince
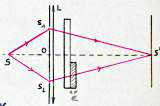 La lame à étudier est collée sur une autre lame placée devant les deux fentes. On laisse même de la colle jusqu’à \(S_1\).
La lame à étudier est collée sur une autre lame placée devant les deux fentes. On laisse même de la colle jusqu’à \(S_1\).
Habituellement \(\delta=a~x/D\) . La présence de la lame introduit le chemin optique supplémentaire \((n-1)~e\) de sorte que : \[\delta=\frac{a~x}{D}=(n-1)~e\]
Au centre \(S'\), on avait \(x=0\), donc \(\delta=0\). On aura à présent \(\delta=(n-1)~e\).
Le déplacement de la frange centrale donne directement \((n-1)~e\). L’expérience est en tout point analogue à celle de Rayleigh.
5. Mesure de l’épaisseur d’une couche mince
 La lame mince à étudier est placée sur la face plane d’une lame de verre AB. Si l’épaisseur n’est pas trop forte, on observe les phénomènes par réflexion en lumière blanche. Par suite des interférences dans la lame mince on observe une teinte qui donne immédiatement l’épaisseur optique de la lame.
La lame mince à étudier est placée sur la face plane d’une lame de verre AB. Si l’épaisseur n’est pas trop forte, on observe les phénomènes par réflexion en lumière blanche. Par suite des interférences dans la lame mince on observe une teinte qui donne immédiatement l’épaisseur optique de la lame.
Supposons que l’indice de la lame soit plus petit que celui du support \(AB\). On a \(\delta=2n~e\) et l’échelle des teintes de Newton donne la valeur numérique de \(2n~e\). Si par exemple la teinte est le pourpre du premier ordre, l’échelle indique la valeur \(0,281\).
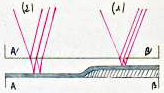 Pour déterminer \(e\) avec plus de précision, on a recours aux interférences à ondes multiples. L’ensemble [AB + lame] est recouvert d’une couche métallique d’épaisseur uniforme.
Pour déterminer \(e\) avec plus de précision, on a recours aux interférences à ondes multiples. L’ensemble [AB + lame] est recouvert d’une couche métallique d’épaisseur uniforme.
L’opération se fait très facilement par évaporation sous vide. On pose sur \(AB\) ainsi traitée une lame de verre \(A'B'\) dont la face en contact avec \(AB\) est bien plane et semi-métallisée.
Par suite des poussières toujours inévitables, il se forme un coin d’air entre \(AB\) et \(A'B'\).
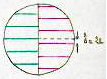 Comme dans les méthodes précédentes, on constate un décalage des franges lorsque l’on passe de la région occupée par la couche mince [1] à la région [2] où il n’y pas de couche.
Comme dans les méthodes précédentes, on constate un décalage des franges lorsque l’on passe de la région occupée par la couche mince [1] à la région [2] où il n’y pas de couche.
Le décalage \(\delta=2e\) donne l’épaisseur \(e\) de la couche mince.
6. Microscope interférentiel en lumière réfléchie
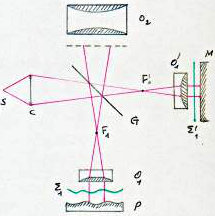 Nous allons décrire le fonctionnement du microscope de Linnik. Le faisceau provenant de l’illuminateur vertical \(\langle S,~C\rangle\) est divisé en deux parties par \(G\) inclinée à 45°.
Nous allons décrire le fonctionnement du microscope de Linnik. Le faisceau provenant de l’illuminateur vertical \(\langle S,~C\rangle\) est divisé en deux parties par \(G\) inclinée à 45°.
Une partie se réfléchit vers le bas, traverse l’objectif \(O_1\), est réfléchie par l’objet \(P\) à étudier, traverse \(O_1\), puis \(G\) et se dirige vers l’oculaire \(O_2\).
L’autre partie transmise par \(G\) traverse \(O'_1\) identique à \(O_1\), se réfléchit sur le miroir de référence \(M\), traverse \(O'1\), se réfléchit en \(G\) et se dirige vers \(O_2\).
Les points \(F_1\) et \(F_2\) sont les foyers respectifs de \(O_1\) et \(O'_1\).
L’onde \(\Sigma_1\) déformée par les irrégularités de surface de l’objet \(P\) et l’onde plane de référence \(\Sigma'_1\) interfèrent dans l’image \(P'\) observée au moyen de l’oculaire \(O_2\).
Si l’image de \(M\) après réflexion sur \(G\) est parallèle à \(P\), le champ est uniforme. Les irrégularités d’épaisseur se traduisent par des variations d’intensité lumineuse. En inclinant légèrement \(M\), son image par \(G\) n’est plus parallèle à \(P\) et il apparaît des franges d’interférences rectilignes.
Les irrégularités d’épaisseur peuvent alors se mesurer par des déplacements de franges. Le décalage \(\delta=2e\) des franges donne la variation d’épaisseur \(e\).
7. La méthode de Twyman-Green
 Si l’on place au foyer d’un objectif corrigé pour l’infini une source lumineuse ponctuelle, l’onde émergente est plane quand l’objectif est bien corrigé des aberrations.
Si l’on place au foyer d’un objectif corrigé pour l’infini une source lumineuse ponctuelle, l’onde émergente est plane quand l’objectif est bien corrigé des aberrations.
L’étude de la surface d’onde permet de connaître et de caractériser les défauts de l’objectif. Pour déterminer la forme d’une surface d’onde, on la fait interférer avec une onde de référence connue.
À partir des franges d’interférences observées, on peut en déduire la forme exacte de la surface d’onde fournie par l’objectif.
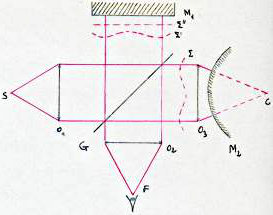
La méthode de Twymann Green est basée sur l’utilisation de l’interféromètre de Michelson, mais le miroir \(M_2\) est remplacé par une surface de référence (le miroir est convexe, centre de courbure \(C\) confondu avec le foyer de \(O_3\) que l’on veut étudier).
\(O_3\) ayant des aberrations, l’onde émergente est déformée. Tout se passe comme si lœil, placé en \(F\), observant des franges d’égale épaisseur entre l’onde plane de référence \(\Sigma''\) fournie par \(M_1\) et \(\Sigma'\) qui est l’onde à étudier.
Si l’objectif \(O_3\) est parfait, \(\Sigma\) est plane et on observe un éclairement uniforme. La différence de marche entre \(\Sigma'\) (symétrique de \(\Sigma/G\)) et \(\Sigma''\) est constante.
En modifiant un peu l’orientation de \(M_1\), on peut observer des franges rectilignes et équidistantes.
On remarquera que \(O_3\) est traversée deux fois, donc les déformations de \(\Sigma\) sont deux fois plus grandes que les déformations à mesurer.

