1. Historique. Tube de Coolidge

Les rayons X ont été découverts par Roentgen en 1895 mais on doit la connaissance de leur nature aux expériences de Laue en 1912. On sait maintenant que tout corps, frappé par des électrons devient source de rayons X.

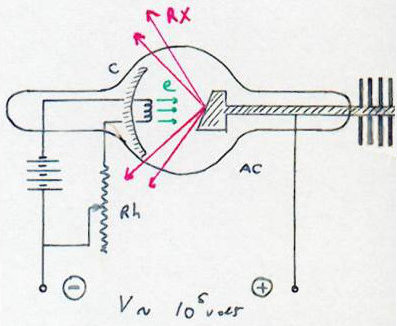La cible anticathode AC est bombardée avec des électrons rapides. La cathode C est concave pour concentrer le faisceau d’électrons.

Lorsque l’électron frappe l’anticathode, il perd de l’énergie, ce qui donne naissance à un photon X. Le rayonnement X est constitué par l’ensemble de ces photons.

On sait que l’énergie du photon est : \[W=h\nu~\leq~ e~V\]

L’intérieur du tube est obscur, car les rayons X sont invisibles pour l’œil, mais on observe une fluorescence verte du tube due à des négatons qui rebondissent sur l’anticathode. Les rayons X se propagent dans toutes les directions à partir du point d’impact des électrons.

Ce point d’impact est porté à incandescence (à cause de l’énergie cinétique des électrons). Aussi l’anticathode est-elle grosse pour assurer un meilleur refroidissement (renforcé par la présence d’ailettes extérieures).

Dans le tube règne un vide aussi parfait que possible. Le rhéostat Rh permet de régler le chauffage du filament, donc le nombre d’électrons émis par la cathode, donc l’intensité du rayonnement X et sa longueur d’onde \(\lambda\) (qui dépend de la nature du métal frappé par les électrons).

2. Diffusion. Effet Compton

Le photon X est une particule dont la masse au repos est nulle : \(m_0 = 0\).

On sait que le photon ne se manifeste que lorsque sa vitesse est celle de la lumière et qu’il atteint une énergie finie \(mc^2\).

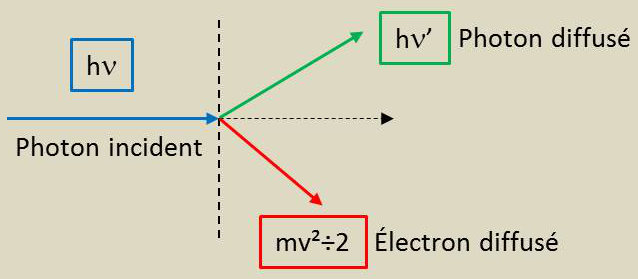Un photon vient frapper un électron au repos en O. Après le choc, le photon est diffusé suivant une certaine direction et son énergie devient \(h\nu'\). L’électron est diffusé suivant une autre direction.

Si la vitesse de l’électron est bien plus petite que celle de la lumière (\(v << c\)), il prend une énergie cinétique : \[\Delta E=\frac{1}{2}mv^2 \qquad[1]\]

D’après le principe de conservation de l’énergie : \[h\nu=h\nu'+\frac{1}{2}mv^2 \qquad[2]\]

Si \(v\) n’est plus négligeable devant \(c\), alors le principe de la relativité s’applique : \[h\nu=h\nu'+(m-m_0)~c^2\]

Pour un photon, la quantité de mouvement est : \[p=mc^2/c=mc\]

Le principe de conservation de la quantité de mouvement en projection sur les axes Ox et Oy donne :

\[\begin{aligned} \frac{h\nu}{c}&=\frac{h\nu'}{c}\cos(\varphi)+mv~\cos(\theta)&&/Ox\\ 0&=\frac{h\nu'}{c}\sin(\varphi)-mv~\sin(\theta)&&/Oy\end{aligned}\]

On élimine \(\nu\) en écrivant que : \(\sin^2(\theta)+\cos^2(\theta)=1\). On obtient ainsi : \[m^2~v^2=\frac{h^2~\nu^2}{c^2}+\frac{h^2~\nu'^2}{c^2}+2~\frac{h^2~\nu~\nu'}{c^2}~\cos(\varphi)\]

En exploitant la relation (relativité) : \[m=\frac{m_0}{\sqrt{1-v^2/c^2}}\qquad\text{ou}\qquad m^2~v^2=m^2~c^2-m_0^2~c^2\]

Et, en ayant tiré \(m^2\) de la relation [2] ci-dessus :

\[\begin{aligned} & m^2~v^2=c^2~\bigg\{\frac{h(\nu-\nu')}{c^2}+m_0\bigg\}^2-m_0^2~c^2\\ & m^2~v^2=\frac{h^2~\nu^2}{c^2}+\frac{h^2~\nu'^2}{c^2}-2\frac{h^2~\nu~\nu'}{c^2}+2h~(\nu-\nu')~m_0 \qquad[3]\end{aligned}\]

Enfin, en identifiant [1] et [3], puis en simplifiant, il vient (relation de la longueur d’onde \(\lambda\) à la fréquence \(\nu\) et la vitesse de propagation \(c\)) : \[\frac{c}{\nu'}-\frac{c}{\nu}=\lambda'-\lambda=\frac{h}{m_0~c}~(1-\cos\varphi)\]

Ainsi la connaissance de \(\nu\) entraîne celle de \(\nu'(\lambda)\). Il suffit de déterminer l’angle \(f\) avec un compteur Geiger recevant le photon diffusé. Il en est de même pour \(\nu'(\lambda)\).

3. Détection

L’effet Compton représente déjà le moyen de détection essentiel, mais nous allons examiner d’autres procédés.

3.1. Chambre de Wilson

Une chambre de Wilson est constituée par un cylindre rempli d’air saturé de vapeur d’eau. La face inférieure est constituée par un piston. Un brusque affaissement de ce piston produit dans la chambre une détente qui permet de rendre visible la trajectoire d’une particule électrisée la traversant à cet instant.

Les ions qui se forment autour de la particule deviennent en effet des centres de condensation pour la vapeur d’eau sursaturée.

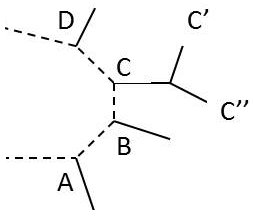Il se forme alors une ligne de brouillard que l’on photographie par la face supérieure de la chambre. On obtient en quelque sorte une matérialisation de la trajectoire par effet Compton.

Les branches A, B, C, D sont des trajectoires d’électrons. En C, C’, C", il y a eu choc d’électrons.

On imagine en pointillé la trajectoire des photons diffusés successifs.

3.2. Chambre d’ionisation

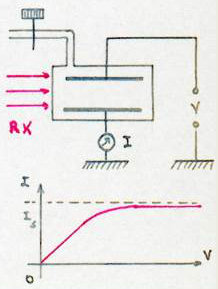Une chambre d’ionisation est une enceinte contenant un gaz et deux plateaux entre lesquels existe une différence de potentiel \(V\).

Lorsqu’un faisceau de rayons X passe entre les plateaux, il apparaît dans le circuit extérieur un courant d’ionisation \(I\).

Celui-ci est d’abord proportionnel à \(V\), puis tend vers une limite \(I_S\), appelée courant de saturation.

Ce courant s’annule en quelques secondes lorsque le rayonnement est supprimé.

3.3. Compteur Geiger-Müller

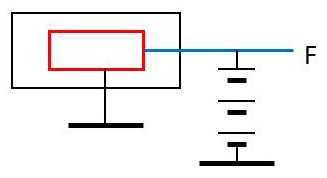Un compteur Geiger-Müller est basé sur le même principe que la chambre d’ionisation, une électrode étant cylindrique, l’autre étant constituée par un fil F. Le cylindre est en aluminium, d’une épaisseur de 0,1 mm environ ; il est négatif et relié à la masse. L’axe F est porté à un potentiel de 1 000 volts.

Quand la particule ionisante pénètre dans le compteur, elle produit un certain nombre de paires d’ions positifs et négatifs qui se déplacent entre les électrodes.

Au voisinage de F, les électrons sont accélérés et acquièrent de l’énergie suffisante pour engendrer de nouvelles ionisations.

Dans un temps très court, F collecte une certaine charge ce qui provoque une subite variation de potentiel donc une impulsion. Celle-ci, convenablement amplifiée est enregistrée par un compteur.

3.4. Compteur à scintillations

Un compteur à scintillations comprend deux parties :

1. une substance transparente (cristal à iodure de sodium avec trace de thallium) dans laquelle se produisent des phénomènes d’ionisation dus à l’absorption d’une particule du rayonnement ;

2. un détecteur qui est généralement un photo-multiplicateur et qui transforme l’émission lumineuse du cristal en courant électrique.

Le passage des rayons X dans un cristal perturbe ses couches électroniques ; leur retour à la configuration stable s’accompagne d’émission de lumière. Il en résulte une suite de scintillations le long de la trajectoire des rayons dans le cristal. Cette lumière vient frapper le photo-multiplicateur dont elle arrache les électrons par effet photoélectrique.

En plus du caractère détecteur, le compteur à scintillations présente l’avantage de renseigner sur l’énergie du phénomène ionisant puisque après amplification, on recueille à la sortie du photo multiplicateur une certaine charge électrique proportionnelle à l’énergie absorbée par le cristal.

3.5. Plaques nucléaires

Une émulsion photographique comprend un mélange de monocristaux de bromure d’argent (AgBr) et de gélatine déposée sur une plaque de verre. Quand le photon traverse l’émulsion, il cède une certaine quantité d’énergie, laquelle altère les monocristaux situés sur la trajectoire.

Quand un photon frappe un des ces grains, on obtient un atome d’argent neutre : \[Ag^+~+~e^-\rightarrow Ag\]

Les grains d’argent (\(Ag\)) qui se forment à l’intérieur du cristal sont rendus visibles par le développement de l’impulsion. Si ces grains sont suffisamment rapprochés (cela dépend de l’énergie dissipée par unité de longueur), ils forment une ligne plus ou moins continue qui matérialise la trajectoire du photon dans l’émulsion.

La connaissance de la longueur des trajectoires permet de connaître l’énergie des particules. Le comptage des grains par unité de longueur permet de connaître la valeur de la masse de la particule ionisante.

3.6. Chambre à bulles

La chambre de Wilson était peu sensible aux particules à hautes énergies. Aussi a-t-on pensé à remplacer le milieu gazeux par un milieu liquide présentant un plus grand pouvoir d’arrêt. En 1952, Glaser a imaginé le dispositif suivant :

Un liquide \((H_2\)) est maintenu dans une enceinte à une température supérieure à la température d’ébullition par application d’une pression convenable. Un abaissement de cette pression favorise l’ébullition.

Quand une particule chargée traverse le liquide, l’ionisation produite le long de la trajectoire entraîne l’apparition de charges électriques qui trouvent comme support des bulles microscopiques de gaz toujours présentes dans le liquide.

Une brusque détente de la pression entraîne un développement des bulles chargées, celles-ci servant de germes à l’ébullition. Une rapide compression arrête la croissance des bulles et restaure la chambre dans son état initial.

La trajectoire de la particule est ainsi parsemée d’un chapelet de petites bulles qui sont éclairées et photographiées à travers un hublot.